丘成桐：人工智能与学“问”

2022 年 11 月 9 日 THU数据派

作者： 丘成桐 ，北京雁栖湖应用数学研究院院长，清华大学讲席教授，求真书院院长，美国科学院院士，中国科学院外籍院士；菲尔兹奖、克拉福德奖、沃尔夫奖、马塞尔·格罗斯曼奖得主。

以下是丘成桐院士于 2022 年 10 月 22 日在“智行中国”系列论坛第一期“迈向教育科学研究新范式”上演讲的讲稿，后半部分内容由“人文清华”讲坛（2022 年 9 月 22 日）的演讲而来。讲稿刊登于《数理人文》（公众号：math_hmat），未经授权，不得转载。

很荣幸在这个会上讲几句话。

从图灵（Alan Mathison Turing）开始，人工智能的发展已经超过四分之三个世纪，它的历史可以说是跌宕起伏，极为生动。

在 2016 年 3 月，AlphaGo 击败围棋高手李世乭的時候，我在重庆见到黄奇帆市长，他兴奋地告诉我这是大事，要改变工业和社会的运作模式。

果不其然，人工智能这门学问迅即成为最有吸引力的学科，在任何政府部门、任何学校、任何公司、都不会错过应用人工智能的机会，投资者亦以此为依据。因此做人工智能的专家都己经腰缠万贯了。本人没有腰缠万贯，所以不可能是人工智能的专家。现在我在这个人工智能大会讲话，可说是滥竽充数。

我今天不讲人工智能，讲的却是如何做好的学问。事实上，这和人工智能也可以勉强拉上一些关系的。毕竟人工智能确是在做前沿科研的工作时，已经成为一个重要的工具。大家开始利用它来搜索一些重要的科研方向，也得到重要的结果。

四年前，我一个朋友迈克尔·道格拉斯（Michael Douglas）来找我。他本来在弦理论做了一流工作后，跑去搞投资赚了一笔，又想回学术界发展人工智能，希望改变数学和理论物理学。他决定从纽约搬到哈佛大学的数学科学中心来大展拳脚，我迅速发现很多科学家都有这样的想法。

上个礼拜，我看到新闻说《Nature》发表了一篇文章《通过强化学习发现更快的矩阵乘法算法》（Discovering faster matrix multiplcation algorithms with reinforcement learning），DeepMind 提出了 AlphaTensor 一个可用于快速矩阵乘法的人工智能系统。这个问题起源于德国数学家沃尔肯·施特拉森（Volken Strassen）在 1969 年的一个重要发现：施特拉森发现两个的矩阵做乘积时，一般算法需要次乘法，他却巧妙地通过不同的组合，只须要次乘法。因此计算机可以节省很多时间。数十年来，很多学者希望对大型矩阵做同样的快速计算，可惜都没有成功。

DeepMind 将这个问题转换为单人游戏，它开发了多个关键组件，包括一个全新的神经网络架构、一个生成有用合成数据的程序以及一种利用问题对称性的方法。它训练了一个利用强化学习的智能体 AlphaTensor，开始时，它没有矩阵乘法的知识。通过学习， AlphaTensor 随时间改进，发现了施特拉森算法，并且发现更多比以往己知算法更快的算法。

这个重要的工作确是人工智能进展的里程碑，开始可以解决一些比较理论的问题，但是离人类思考的能力还是相当的遥远。

首先我们知道施特拉森走的第一步是突破，因为以前没有人猜到这个可能性！假如没有他这一步，没有人会去问快速矩阵乘法的可能性，人工智能更不会，这个研究便无从开始！问好的问题是好的科学的开端！但是直到目前为止，人工智能还没有能力问一个既有意义又有深度的问题。

除了问有意义的问题之外，人工智能也没有办法知道它的算法是否最佳？事实上，来自奥地利林茨约翰·开普勒大学的研究人员考尔斯（Manuel Kauers）和穆斯鲍尔（Jakob Moosbauer）在其最新工作中表示，他们已经打破 AlphaTensor 的矩阵乘法记录。他们开发了一种以 95 步执行矩阵乘法的方法，比 AlphaTensor 的 96 步记录少了一步，此前的记录为 98 步。论文预印版于 10 月 13 日发布在 arXiv 上。

Kauers 和 Moosbauer 的论文预印版（arXiv:2210.04045v3）

我们现在讨论人类学习科学的目标和方法，人工智能真的想和人类思维竞争，恐怕也须要知道人类在科学研究上成功和失败的原因。我们要找寻大自然和我们见到的所有现象的规律，讲到规律，我们就必须要重视逻辑。

从目前来说，我们现在用的逻辑是由希腊人发展下来的三段论证的方法，这个方法不太可能被代替。有了清楚的逻辑系统以后，我们去观察各种现象，然后去猜测、去找规律、再去推导这些规律。

希腊哲学家泰勒斯（Thales）的理论可以看为科学的开始，他也是古代第一位天文学家、第一位物理学家和第一位几何学家。他用手杖观影的方法来测量金字塔的高度。他应用逻辑的方法来得到科学的结论。毕达哥拉斯（Pythagoras）可能是第一个写下定理的严格证明的数学家。两百多年后，欧几里得欧几里得（Euclid）作《几何原本》，将当时已知的几何定理通过公理组合起来。这几位数学家和哲学家的思维影响了西方科学发展达两千多年，也可以说是东西文明的第一个分歧点。

我们需要问一个简单的问题：毕氏定理或者是勾股定理的特殊情形，在古巴比伦、古埃及、古印度、古代中国都可以见到它们的雏形，但是要到希腊人才想到它的一般公式，并且去证明这个公式。这是伟大的突破，机器做得到吗？从几百个平面几何定理中，找到其中的精髓，设立五条公理，推导出这些定理，机器应该可以做得到，但是如何去做呢？人工智能要想得到智慧，我觉得这是重要的一步。

有趣的是，希腊人又发现：在这些公理中，把关于长度的观念去掉以后，可以产生一个新的几何学，叫做射影几何学（projective geometry），影响深远，以后它和代数结合，产生了多姿多彩的代数几何。我们可以训练机器去构造新的结构吗？

射影几何学第一个定理 —— 帕普斯定理：设、、、、和为平面上六条直线，如、、三点共线，、、三点也共线，则、、三点亦共线。

如今在科学研究时，我们见到一大堆数据和现象，我们有没有办法通过机器去找到产生这些现象的基本理由？正如牛顿当年找到力学的三大定律一样。现在很多科学家都会做建模的工作，但是取样往往不够。我希望机器可以大量搜索各门学问，通过类比的方法来找他们的共通点。

我从前说过：“《诗经》中的赋比兴的手法，也是数学家常用的手法，机器可以学习吗？”

机器应该试图通过逻辑来比较不同学科相似的研究，找到共同点，试图将不同的学问融合。就如麦克斯韦（Maxwell）通过方程式将电学和磁学联合一样！

现代数学的一个伟大转变是复数的发现和它的应用。刚开始时，大数学家们都对它畏惧，但是欧拉（Euler）还是写下他伟大的公式：

这个公式成为现代数学的基础，波的描述要靠它，量子力学的描述也要用它。数学家花了二百多年才能消化复数的观念，现在它是我们看到的大自然的一部分！在熟知的实数世界里，机器有办法突破旧的观念，看见复数的威力吗？

在几何发展的近代历史上，有几个重要的跳跃：

第一次是坐标的引进，产生了解析几何。
第二次是微积分的引入。
第三次是黎曼为了研究引力和其他物理现象引入的黎曼几何。到了 20 世纪黎曼几何成为广义相对论的基础。
第四次是外尔（Hermann Weyl）和嘉当（Élie Cartan）引入的规范场（嘉当叫它为联络（connection）理论）。
第五次是近半个世纪来，量子场论和弦理论被引入到几何后，新的概念使几何产生了大变化。

每一次跳跃都有新的观念的引进和开发。我们可以想象人类如何做得到，而机器做得到吗？在某种意义下，这些过程可以看为是一个突变。可以和数学上的混沌（chaos）的看法类似，所以机器是否应该考虑混沌的观念。

20 世纪的科学和量子力学有密切的关系，量子力学的思维是人类思维的大跳跃，但是量子科学的物理和数学基础直到今天都还没有完成。量子场论遇到很多无穷大的数学问题：物理学家凭他们的直觉，似乎是从无到有，得到有用的物理数据，而居然可以验证实验到小数点后十多位，使人佩服。

无论从人的智慧和机器的能力来看这些伟大的成就，我们都需要去了解它们成功的因素。

18 世纪时，欧拉对发散级数有很深入的直观处理方法，黎曼通过复变函数的方法解释了欧拉的直觉，对于量子场论的发散问题也得到了一定的解释，但是距离目标还相差甚远，仍需要努力。

现代量子场论的思维对于机器学习有帮助，如何将这些对自然界有深度的理念组合起来，有系统地学习，必定会有意义的。

以上只不过找了历史上一小部分有意思的发展，为什么我提出这些事情，因为牛顿讲过：“如果说我看得比别人更远些，那是因为我站在巨人的肩膀上。”这绝对不是谦虚而已。牛顿做的很多东西，先前的科学家、数学家也曾考虑过，只是没有他考虑的这么完美，后世就不再提及了。事实上，牛顿的工作都是在前人的基础上做出来的。

我们要考虑整个学问向前走的方向到底是什么，应该如何去认识数学的内在结构，这是许多大数学家常常思考的问题。

大学问家往往会提出很多问题，这一点很重要。但中国的科学家不大爱问问题，不大问自己原创的问题，更多的是解答别人的问题。虽然解答的不错，但这不见得是数学和科学的真髓，重要的是要找出自己的方向。

希尔伯特二十三问

在数学历史上，一个非常重要的问题集，就是希尔伯特 23 问。1900 年 8 月 8 日，这位德国数学家在巴黎国际数学家大会上做题为《数学问题》的演讲。希尔伯特认为，从 19 世纪进入 20 世纪，提出一些重要的问题，对于推动学科进步的作用毋庸置疑。他说，一个学科能够产生大量重要问题，才能保持它的活力。他是当时最伟大的数学家，吸引了不少人听这个演讲。这 23 问基本上引领了数学界五十年的发展。23 问不是全部由他提出，也有从前大数学家的问题，比如黎曼等。他将重大的问题收集起来，又增加了自己的问题，这是希尔伯特引领一代风骚的重要时刻。这些问题至今并没有全部解决，但其中部分问题的解决，就已经促发了数学学科重要的发展。

丘成桐一百二十问

1978 年，我在普林斯顿高等研究院组织几何年特别会议 —— 微分几何论坛，带领一批数学家、几何学家研究几何方面主要的方向。会议最后几个礼拜，我徇众要求，作为领导的几何学家提出几何方面最重要的问题。我于是提出了 120 个问题，虽然我的问题无法跟希尔伯特 23 问相提并论，但还是很有意义。

为什么我要问这些问题？因为 120 问对当时几何学遇到的困难主要在什么地方进行思考，同时指出学科向前走的方向，以及解决后会产生什么重要的结果和影响。这些问题到了今天，大概三分之一被解决，值得高兴的是，大部分都是正面的解决，基本印证了猜想的方向是重要的、是正确的，很多数学家为了解决这些问题也得到了很好的结果。我到现在还是很高兴，自己做到了这个事情。

一些好的问题短期内不见得有很大的影响力，因为需要花时间去消化、去思考。但是，这些问题一经提出，往往会影响到数学中某些学科的方向。这 120 个问题促成了一个重要的学科“几何分析”的发端。很多好的几何学家对这些问题都有兴趣，推动了这个学科的发展，再次印证了问问题是很重要的事情。

但是，问题有好的，也有不好的。什么叫好的问题？好的问题就是，思考这个问题本身，就发展出一系列的想法、催生出一系列文章。无论最终是否解决，仅仅推敲、研究这个问题的过程都很重要。好的问题一般简洁、很漂亮，可以解决数学上很多疑难。解决了它，所在领域里许多问题都会随之解决。这就好像在长江里面有一块巨石，将巨石挪开，水流就会顿时变得更顺畅，好的问题会让人豁然开朗。

我现在来讲讲当年我提出的 120 个问题中的两个题目，虽然它们到今天还没有全部解决，但是很多学者花了不少功夫，也得到很多重要的发展。

能否听出鼓的面积？

我要举例的第一个问题是关于声音和几何的关系。古希腊时代，人类就认识到声音由一些基本音组合而成。无论弹钢琴或是打鼓，敲击产生不同频率的波动，发出声音。波动由多个基本波组合而来，我们上音乐课时都知道基本音级 Do Re Mi Fa Sol。科学家对基本音级、基本波都很感兴趣。每个基本波有固定的频率，频率则由鼓的谱计算得到。波动产生很漂亮的图形，下面的图片显示了不同的波动，有高、有低，还有不动的地方。对于这样漂亮的几何，几何学家十分重视。

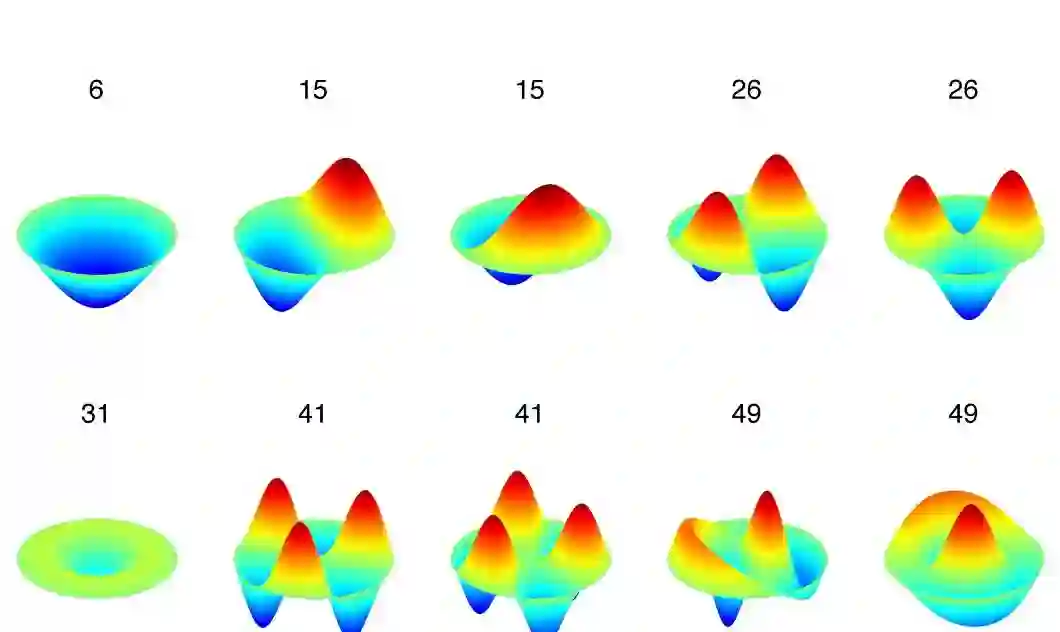
1966 年，杰出概率学大师马克·卡茨（Mark Kac）指出著名的几何学家博赫纳（Salomon Bochner）提过一个问题：我们可否听出鼓的形状？

这一问题的思想可以追溯至 1910 年。当时，量子力学刚刚萌芽，物理学家洛伦兹（H. A. Lorentz）在哥廷根大学演讲时，提出了一个有趣的数学问题：是否可以通过鼓声的谱和频率估算鼓的面积？希尔伯特对于这个问题很感兴趣，但他认为这个问题太难，他有生之年，不可能看到这个问题的解决。

当年，希尔伯特在德国哥廷根大学培养了一大群优秀的学生，其中不少成为 20 世纪著名数学家。外尔就是其中之一。外尔是一位非常重要的学者，他开创了今天高能物理中的规范场理论。过了一年，外尔就把这个问题解决了。下面这个公式后来被称作外尔公式，是以前所有谱的数目，除以的幂，越大时，极限与面积乘以一个常数一样。

外尔解决问题的思路和方法很重要。他认为，谱越来越高，按照量子力学的观念，即谱的观念，可以推测到局部的几何变化，从而推出外尔方程。这是个很重要的方程，对今天的数学仍然有重要的影响，对于数论和几何也十分重要。

外尔的思路和方法还可以向前追溯。欧拉跟黎曼都是历史上最伟大的数学家，我想很少人能够否认这句话。欧拉研究了一个很简单的问题，当是正整数时，下列式子的和是多少？

他花了很多功夫研究这个问题，产生了重要的泛函方程。黎曼将其推广，写下了著名的黎曼函数。

他发现这个函数十分漂亮，可以在整个复平面上定义，就是说容许为复数。黎曼发现这类复函数具有对称性，有较明确的零点和极点，以及不明显的零点，黎曼猜测这些不明显的零点都在一条直线上，同时这些零点的分布和素数的分布，有密切的关系。这是个划时代的工作，这个函数影响了数论的发展，也影响了外尔的工作。

外尔推广了黎曼函数的思想到一般的空间，用以研究“听鼓声估算面积”这一问题，并最终解决。他将黎曼函数中的整数改为谱，从而将面积与频率联系起来。鼓声的谱越来越高，可以推知局部的几何，得出一个很重要的结论：面积跟频率有很密切的关系。

能否听出鼓的面积 —— 这个问题由洛伦兹从物理现象出发，提出问题，最终由外尔解决。这个问题简洁、自然、有趣，解决的方法引发了几何上不少重要的发展。

谱可以视为几何图形的量子讯息，我们事实上获得了量子讯息和几何的关系。谱向无穷增大时得到局部的几何讯息，包括曲率、面积元等；谱小时，得到几何的拓扑或是宏观讯息。因此，几何学家对几何图形最小的谱也有浓厚的兴趣。

要了解卡茨的问题，需要知道所有谱的几何意义，因此解决起来更为复杂，至今没有全部解答。

波节线的长度猜想

视频制作：人文清华讲坛；鸣谢：清华大学实验物理教学中心

有趣的是，从克拉德尼（Ernst Chladni）实验中，我们可以看到，尽管波节线的图案出现很多变化，但波节线的长度似乎不太变动。

1978 年，我提出一个问题：谱很大时，波节线的长度如何变化？我发现，打鼓时不变动的线的长度加起来，可以用谱本身的量来估计。基本上，波节线的长度跟谱成正比。我花了很多功夫提出这个猜想。

一方面，打鼓时，波节线变化得很厉害，但长度这个基本量却变化不大。其二，我计算了很多例子，发觉其长度是在附近变动的。于是得到结论：它应该满足下述不等式

这个不等式到目前为止仍然是关于波节线一个重要猜想，引起了很多数学家、几何学家、物理学家以及数学分析研究人士的关注。这个猜想，到现在差不多 50 年了，其中一部分被证明是对的，但仍然没有全部解决。假如诸位感兴趣，应当试着去解决它。这个问题很有意义，该不等式中有两个常数和，它的几何意义十分值得我们去摸索。

作为一个几何学家，我对洛伦兹、外尔的问题很感兴趣。他们通过谱和频率的变化来估算面积，我则注意到了鼓不动的地方有什么变化，这个猜想的思想在很多地方都用得到。外尔的研究基于大的情况下开展。1974 年，我开始研究当小的时候，它和几何的关系可否刻画出来，这其实是一个很重要的问题。我在研究的时候看了很多不同的书，发现谱是量子力学中重要的观念，当谱很大的时候，它与局部几何有很密切的关系；当谱小时，它则跟宏观的几何有密切的关系。

数学中的赋比兴

完成上述猜想的过程中，基本方法是，比较两个完全不同的观念，一个是几何的观念，一个是量子力学的观念。这种手法其实是数学研究中的惯用手法。数学是很奇妙的学问，它是一个讲究推理、讲规则的学问。我们可以通过它们的规则和思想来做比较，就可以得到有意义的猜想。

诗经里讲“赋比兴”，我认为与我们做数学也有着很密切的关系。所谓 “比”，即用不同的景物类比，比如杨柳代表离别或者美人的腰枝。讲起离别，不免想起《诗经》写道“昔我往矣，杨柳依依。”周邦彦笔下“长条故惹行客。似牵衣待话，别情无极。”以及柳永的名句“杨柳岸，晓风残月。”而说道美人的腰肢，则忆起张先的“细看诸处好。人人道，柳腰身。”这都是缘于柳条细而柔所作的类比。更有温庭筠的“柳丝长，春雨细，花外漏声迢递。”，周邦彦描写“长亭路，年去岁来，应折柔条过千尺。”

这种种不同的比较，也是数学上常用的手段。数学研究者们应该考虑这个思路，不能只做题目，看到数字就是数字，看到方程就是方程，它们中间有很多可以比较、可以关联之处。

好问题从何而来？

好问题从什么地方来的，怎样才能解决它？我们首先要了解不同的观点，就像我提到几何的观点与量子力学的观点。历史上，重要的大学问的完成，往往是不同学问之间碰撞产生火花促成的。

外尔是一个伟大的数学家，也是一个伟大的物理学家，他在量子力学和几何学之间搭建了一个桥梁。因这个桥梁，孕育出一批很好的数学家，一个全新的路径。找到自己的方向，对我们来讲是很重要的事情，也是问出好问题的重要途径。

还有一个途径，可以产生好的问题。要解决一个大问题时，往往要有很好的工具。工具的发展是不断精益求精的过程，每个新工具又促进学问继续发展，新工具让我们看到不同现象，提升我们看待问题的深度，又促发我们进一步发展工具。工具越多，越能产生更深刻的、更有效的解决问题的方法。每一次工具的进步，都带动有意义的、重要的、突破性的学问的发展。

在伽利略时代，他看到地球是太阳系里的行星，这引发了牛顿力学的发展。此后，人类看得更远。到了 20 世纪初期，我们了解到太阳系外还有银河系，以及不同的星云。每一次跳跃都是伴随着“望远镜”这个工具不断发展的。数学上也同样如此，我们在解决问题时，最初的工具远远不够，还要不断发展新的工具。

1670 年出版的丢番图《算术》一书里，包括了费马的评论，被称为他的“最后定理”（ Observatio Domini Petri de Fermat ），死后由他的儿子出版。

费马猜想的解决也是如此。费马猜想距今已经有 300 多年的历史。直到 30 年前，英国大数学家怀尔斯（Andrew Wiles）才解决了这个问题。在怀尔斯之前，几百年来，大数学家们都有兴趣解决这个问题。费马和欧拉就解决了时的情形，使用了椭圆曲线的方法，得出很重要的结果，但是仅限于的情形。19 世纪，德国数学家库默尔（Ernst Kummer），以为自己可以解决费马问题，结果没有成功，但引入了代数中的重要概念，即理想（ideal），带动解决了一大批问题，但还是没有根本解决费马猜想。到了 20 世纪，出现了更多不同的方法，其中一个重要的方法，是由日本数学家谷山丰（Yutaka Taniyama) 、志村五郎（Goro Shimura），以及法国大数学家韦伊（André Weil）提出的谷山-韦伊-志村猜想（Taniyama-Weil-Shimura conjecture），成为解决费马猜想的重要工具，最终由怀尔斯解决了这个 300 余年的题目。

欣赏数学之美的同时，我要欣赏数学美与真背后的规律。了解了它的美和规律，通过不断地比较，提出重要的、具有开创性的问题。而一个学科重要的问题，只有在不断学习中，才能慢慢体会。

何为伟大的工作？

伟大的数学家都有一套自已对学问的看法（Philosophy），这些系统的、深邃的、崭新的观点给古老的数学注入新的活力，因而产生一系列有意义的问题。正如西方歌剧《浮士德》、中国古典《红楼梦》一样，都是由不同部分组成，每个部分又自成一格，有其独特之处，但无论牡丹、绿叶，终须大师写下纲领，方可将零散的部分组合一番，成为一幅瑰丽的图画。

所以，我们要创立一个这样的纲领。在这纲领的指引下，将各个不同的学科分支放在一起，才能构建出一个宏伟的大厦！一般来说，要完成这种宏观的看法，并非一人一时之工，一人一时之问，有时长达一个世纪，才看得出这些纲领的威力。

1854 年，黎曼在伟大的就职演讲《论作为几何学基础的假设》中，给出了几何学的一个纲领。他通过物理学中的等价原理建造了新的内蕴几何，完成了广义相对论重要的部分。20 世纪初期，外尔开发李群的表示理论和规范场理论，成为现代理论物理的基础。韦伊则在上世纪定下用代数几何作为工具研究数学的方向，完成了数学历史上一个伟大猜想 —— 韦伊猜想（Weil conjecture）。我的朋友朗兰兹（Robert Langlands）五十多年前提出著名的朗兰兹纲领（Langlands program），用群表示理论研究数学，产生了一大批重要的方向和问题。这些工作可谓大气磅礴。

凡是伟大的工作，都是饱读文献，“望尽天涯路”得来的结果。我在上世纪 70 年代开创现代几何分析时，主要的信念是用函数和定义的微分方程来描述空间，又通过几何来了解函数和微分方程。我提出的 120 个问题就是这样产生的。

何为一流的问题？

好的问题一定要有深度、有趣味、并且简洁。数学与文学有相通的地方。文学上，我们通过简洁的语言描述我们看到的现象。数学也喜欢简洁。一般来讲，假如命题不够简洁，则难以深入，但深入的问题也不一定很简洁。总的来说，一个好的数学问题，要有深度、简洁、漂亮、有趣。

什么叫深度？深度就是解决一个问题后，可以引领新的方向，看到更深远的图景。比如，我们爬到一个高山上，看到更广阔的前景和崭新的疆域。

什么是简洁、漂亮？在数学上，大自然的美景可以通过很简单的方程解释清楚。当年牛顿方程、爱因斯坦方程、狄拉克方程，都是极简洁的，总结了大自然之中很多很漂亮的现象，包含了大自然的奥秘，这当然是很漂亮的事情。

文学用很简单的语言描述大自然的景色，与我们产生心理的共鸣。好的数学，也能在我们心里产生共鸣。当年，我听到卡拉比的讲话后，心里产生很大的震撼。我觉得如果能够了解这个猜想，我将解决数学里一大片问题。

有深度的学问不一定简洁，往往还需要改进。第一流的问题一定要有深度，同时本身很漂亮，很有意义，让人很有兴趣。庞加莱猜想、费马问题、卡拉比猜想，都是有深度、有兴趣、很简洁的问题，这是大问题，一流的问题。

有人问我第二流、第三流的问题是什么样，我不好举例。总的来说，研究数学在于研究数学的深度、意义和内容。几十年来，我们看到有些重要的问题被解决了，最出名的是四色问题（Four color problem），即一张地图只需四种颜色标记就足够。这是很出名的大问题，大概 40 年前就被解决了。解决方法的最后几步，是计算机来完成的。当然，其解决方法基本正确，但我们对这个问题本身的意义，其组合意义、几何意义，到现在还没有得到深入的了解。因此，我认为这个问题其实没有全部解决，希望以后能够更深入地了解它，问题才算得到真正的解决。现在很多数学问题，尤其是应用数学的问题，都是通过计算机算出来的，有时候可能是对的，有时候可能是不对的。这其中最大的问题是，我们对问题的结构，对整个学问的结构并不了解，这些不能算是第一流的答案，也不可能在工业界做出引领风骚的一流技术。了解一个数学问题时，我们应该深入、清楚地了解它的结构和前景。

有一些问题，趣味性比深度更大。我也做过类似的问题，比如我 48 年前完成的一篇小文章，当时也有很大的影响。我证明一个空间，曲率是大于 0 时，只要不是紧致的，其体积无穷大。这是一个很有趣的命题，证明起来也不太难。虽然不算是个很有深度的问题，但是“虽小道，必有可观者焉”，小道往往可以成为大道的起点。我们说问题只要有趣味，都可以算是一个好的问题。

如何培养本土的大师？

最后，我们谈谈如何培养大师。我们希望学生有视野、要用功、要发问，这都是很重要的训练。有视野很重要，跑到高山上以更广阔的视野看世界。但如果没有爬山的工具，就只能远远的望，因此掌握工具也很重要。

70 年代，我做了不少问题，为了解决问题，我学了很多数学，工具就是从学习中得到的，并不是随便得出来的。我看了很多量子力学的书、几何的书，从中得出了很多结论。因此，工具必不可少，否则都是空谈。我希望大家做学问的时候，一定要一步一步扎实的走，才能做出重要的问题。但无论如何，问问题是一个最重要的步骤，问问题之后还要能够解决它，就算不能解决，也要探索出新的工具、新的方向。

今天，中国基础科学想要发展，最主要的是问问题。中国的数学家都很不错，但尚且没有出现一批真的有能力问出重要的问题的数学家们。我们要训练现在的年轻人，培养他们找出重要问题的能力。通过问问题能够产生一些重要的工具，利用这些工具将问题解决之后，你的心里会很高兴。

问一个有意思的问题，同时解决它，假如解决的方法是前人没有走过的路，这个过程会更令人满足，比成为世界上最富有的人还要高兴。这是我做学问的感想，我觉得从中有很大的收获。

我今年 73 岁了，但是我这一辈子走过的路我觉得很高兴。很多媒体问我，当年完成卡拉比猜想时感受如何？我引用了晏几道的两句词，“落花人独立，微雨燕双飞。”形容我当年的心情。当年我打算解决卡拉比猜想的时候，事实上没有人同意这个猜想是对的。到了落花结果的时候，就是我终于解决它的时候，我自己一个人独立地完成它、欣赏它，觉得很满意。所谓“微雨燕双飞”是说，在微雨之中欣赏我完成工作，觉得自己与大自然融合在一起。我做的图形，我抱有的想法与大自然相融。

我想，做好学问的学者都有这个想法，好的数学完成了以后让人觉得满足。这不是骄傲，就像画家完成一个漂亮的图画之后的心境。我鼓励年轻的学者，好好的想，学好的学问，问好的问题，为了探索大自然的奥秘努力，为了寻找大自然中的规律，探讨学问，很快就会产生一大批第一流的学者。

今天就讲到这里，谢谢！■

推荐阅读