DeepMind攻克50年数学难题！AlphaZero史上最快矩阵乘法算法登Nature封面

来源：新智元
  本文为约4603字，建议阅读9分钟
本文介绍了第一个用于为矩阵乘法等基本计算任务发现新颖、高效、正确算法的AI系统——AI围棋大师AlphaZero

【导读】DeepMind碾压人类高手的AI围棋大师AlphaZero，下一个目标是数学算法！现已发现50年以来最快的矩阵乘法算法。

下围棋碾压人类的AlphaZero，开始搞数学算法了，先从矩阵乘法开始！

 

在昨天DeepMind团队发表在Nature上的论文中，介绍了 AlphaTensor，这是 第一个用于为矩阵乘法等基本计算任务发现新颖、高效、正确算法的AI系统 。

 

论文链接：

https://www.nature.com/articles/s41586-022-05172-4.pdf

 

AlphaTensor为一个 50 年来的悬而未决的数学问题找到了新答案：找到两个矩阵相乘的最快方法。

 

先看看这研究都说的啥。

 

提高基础计算算法的效率 一直都是学界热点，因为它会影响大量计算的整体速度，从而对智能计算领域产生多米诺骨牌式的效应。

 

上一张图，来看看AlphaTensor有多「能干」。

 

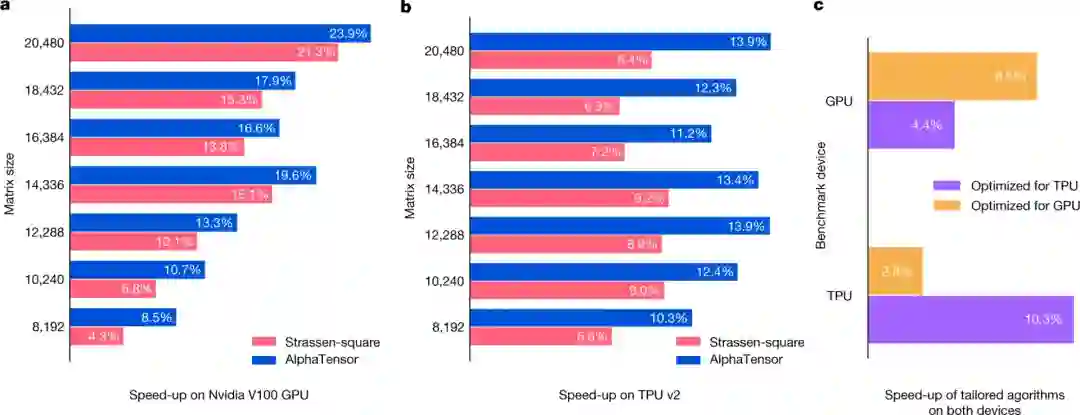
图a,b为AlphaTensor发现的算法在GPU (a) 和 TPU (b)上的加速百分比表现，针对大小为 8,192 × 8,192的矩阵乘法进行了优化

 

矩阵乘法就是这样一项原始任务，从神经网络到科学计算程序，它都是不可或缺的部分。

 

然而，算法发现过程的自动化是复杂的，因为可能的算法空间是巨大的。

 

DeepMind这次发布了一种基于AlphaZero的深度强化学习方法，用于发现任意矩阵乘法的有效且可证明正确的算法。

 

这个算法空间包含 标准矩阵乘法算法 和 递归算法 。

 

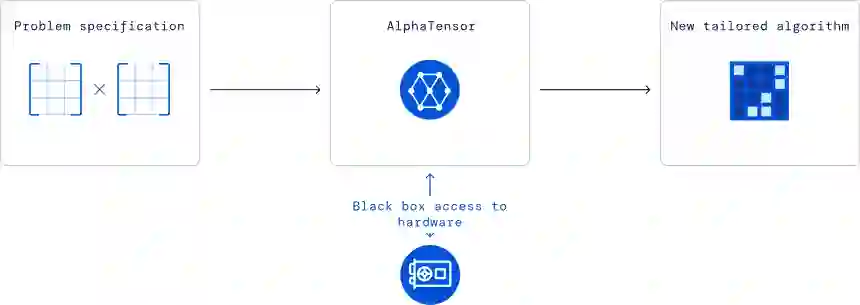
DeepMind将矩阵乘法算法发现过程（即张量分解问题）制定为一个单人游戏——TensorGame。

 

AlphaTensor 建立在 AlphaZero 之上，训练了一个神经网络来指导规划过程，以搜索有效的矩阵乘法算法。

 

我们的框架使用单个智能体来分解各种大小的矩阵乘法张量，从而产生跨各种张量的学习分解技术的转移。为了解决游戏的挑战性，AlphaTensor 使用专门的神经网络架构，利用问题的对称性并利用合成训练游戏。

 

AlphaTensor可扩展到比人工或组合搜索所能达到的算法空间大得多的算法空间。

 

事实上，AlphaTensor 从零开始发现了许多可证明正确的矩阵乘法算法，这些算法在标量乘法的数量方面改进了现有算法。

 

结果表明，AlphaTensor发现的算法在许多矩阵规模上都优于最先进的方法。

从围棋到矩阵乘法：AlphaZero「出圈」

矩阵乘法，学过线性代数的都熟悉，作为矩阵变换的基础运算之一，矩阵乘法是线性代数的基础工具，不仅在数学中有大量应用，在应用数学、物理学、工程学等领域也有广泛使用。

 

作为构成数学算法的基础运算之一，矩阵乘法的应用史长达数千年。

 

早在古埃及时代，人们就创造了一种无需乘法表的两个数字相乘的算法，希腊数学家欧几里德描述了一种计算最大公约数的算法，这种算法至今仍在使用。

 

 

在伊斯兰黄金时代，波斯数学家Muhammad ibn Musa al-Khwarizmi设计了新的算法来解决线性和二次方程。事实上，al-Khwarizmi的名字被翻译成拉丁文为Algoritmi，这就是今天英文「算法」一词的前身。

 

但是，尽管今天人们对算法非常熟悉，但是，发现新算法的过程是非常困难的。

 

在我们今天发表在《自然》杂志上的论文中，我们介绍了 AlphaTensor ，这是 第一个用于发现新的、高效的、可证明正确的矩阵乘法等基本任务算法的AI系统 。这为数学领域一个长达50年的开放性问题——如何寻找两个矩阵相乘的最快方法——给出了答案。

 

这是DeepMind推动科学发展和利用AI解开最基本问题的又一次实践。AlphaTensor建立在AlphaZero的基础上，后者是一个在国际象棋、围棋和象棋等棋类游戏上表现超出人类的智能体，从下棋，到解决半个世纪以来的数学算法，AlphaZero是如何做到的？

打破矩阵乘法50年最快记录

矩阵乘法是代数中最简单的操作之一，通常在高中数学课上教授。但在课堂之外，这个不起眼的数学运算在当代数字世界有着巨大的影响力，在现代计算机中无处不在。

 

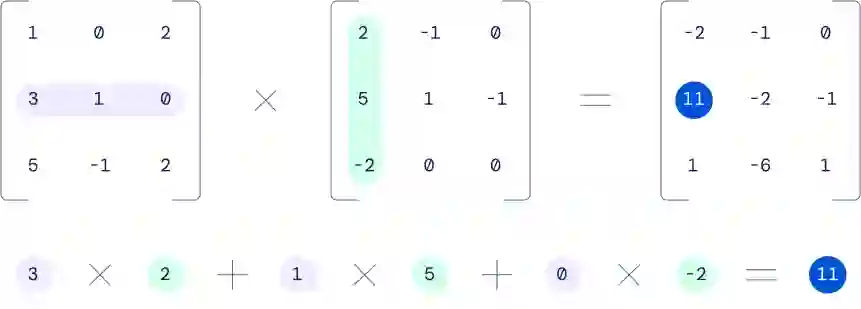
3*3矩阵相乘的计算

 

矩阵乘法被用于处理智能手机上的图像，识别语音命令，为计算机游戏生成图形，运行模拟以预测天气，压缩数据和视频以在互联网上共享等，应用极为广泛。

 

世界各地的公司花费了大量的时间和金钱来开发计算硬件，以有效地进行矩阵乘法。因此，即使是对矩阵乘法效率的微小改进也会产生广泛的影响。

 

几个世纪以来，数学家们认为，标准的矩阵乘法算法是人们在效率方面所能达到的最佳状态。

 

 

但在1969年，德国数学家Volken Strassen震惊了数学界，他表明确实存在更好的算法。

 

 

 

此前的矩阵乘法的标准算法与Strassen的算法相比，后者在乘2x2矩阵时少用了一个标量乘法（7次而不是8次）。就整体计算效率而言，乘法比加法重要得多。

 

通过研究非常小的矩阵（大小为2x2），他发现了一种巧妙的方法来组合矩阵的条目，从而产生一种更快的算法。尽管经过几十年的研究，这个问题的更大版本仍然没有得到解决--以至于人们不知道如何有效地将两个小到3x3的矩阵相乘。

 

在Nature的新论文中，我们探讨了现代人工智能技术如何推进新矩阵乘法算法的自动发现。AlphaTensor发现了在许多矩阵大小上比现有技术水平更有效的算法。我们的人工智能设计的算法优于人类设计的算法，这是在算法发现领域的一个重大进步。

AI推动算法发现的自动化

首先，我们将寻找矩阵乘法的有效算法问题转化为一个单人游戏。 在这个游戏中，棋盘是一个三维张量（数字阵列），记录了当前算法离正确的程度。

 

通过一组与算法指令相对应的允许移动，玩家试图修改张量并将其条目清零。当玩家成功做到这一点时，对于任何一对矩阵来说，都会产生一个可证明正确的矩阵乘法算法，而其效率则由将张量清零所需的步骤数来体现。

 

这个游戏具有令人难以置信的挑战性-- 要考虑的可能算法的数量远远大于宇宙中的原子数量 ，即使是对于矩阵乘法的小案例。与几十年来一直是人工智能挑战的围棋游戏相比，我们的游戏每一步可能的动作数量要大30个数量级。

 

从本质上讲，要玩好这个游戏，相当于要在「巨大的干草堆中找出最小的那根针」。

 

为了应对这个明显不同于传统游戏的领域的挑战，我们开发了多个关键组件，包括一个新的神经网络架构，其中包括特定问题的归纳偏见，一个生成有用的合成数据的程序，以及一个利用问题的对称性的配方。

 

然后，我们利用强化学习训练了一个AlphaTensor智能体来玩一个单人游戏（Tensor Game），开始时没有任何关于现有矩阵乘法算法的知识。

 

 

AlphaTensor在TensorGame中的目标则是在有限因子空间内找到张量分解 (Tensor Decomposition)。

 

在介绍张量分解之前，我们可能需要先简单地了解一下张量是什么，然后再考虑张量分解有什么用途。

 

从初中到大学，我们接触最多的可能只是标量（scalar）、向量（vector）和矩阵（matrix），而张量则不那么常见，但实际上，标量是第0阶张量，向量是第1阶张量，矩阵是第2阶张量，第3阶或阶数更高的张量被称为高阶张量（higher-order tensor），一般提到的张量都是特指高阶张量。

 

 

我们也知道，在一个矩阵中，某一元素的位置可以说成“第几行第几列”的形式，要表达某一元素的位置需要两个索引构成的组合 ，类似地，在一个第3阶张量里面，表达某一元素的位置需要三个索引构成的组合 。

 

在处理稀疏矩阵和稀疏张量时，用索引来标记元素的位置会带来很多便利。另外，阶数的张量可以理解为矩阵的维泛化，在这里，阶数其实就是空间维度（spatial dimension），张量可以被视为多维数组。

 

张量分解从本质上来说是矩阵分解的高阶泛化 。

 

对矩阵分解有所了解的读者可能知道，矩阵分解有三个很明显的用途，即降维处理、缺失数据填补和隐性关系挖掘，而张量分解也能够很好地满足这些用途。

 

为了解决TensorGame并找到有效的矩阵乘法算法，我们开发了一个DRL智能体AlphaTensor。

 

通过学习，AlphaTensor随着时间的推移逐渐改进，重新发现了历史上的快速矩阵乘法算法，如Strassen的算法，最终超越了人类的直觉领域，发现的算法比以前已知的更快。

 

 

 

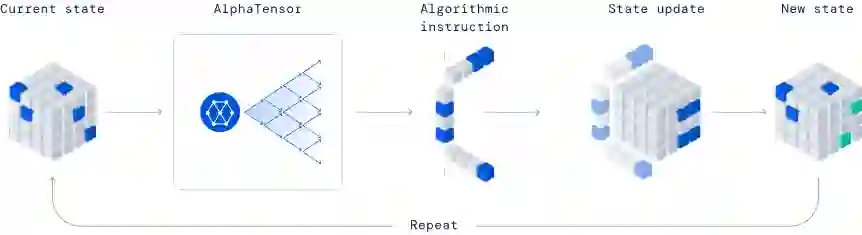
由AlphaTensor玩的单人游戏，目标是找到一个正确的矩阵乘法算法。游戏的状态是一个由数字组成的立方体数组（显示为灰色为0，蓝色为1，绿色为-1），代表着要做的剩余工作。

 

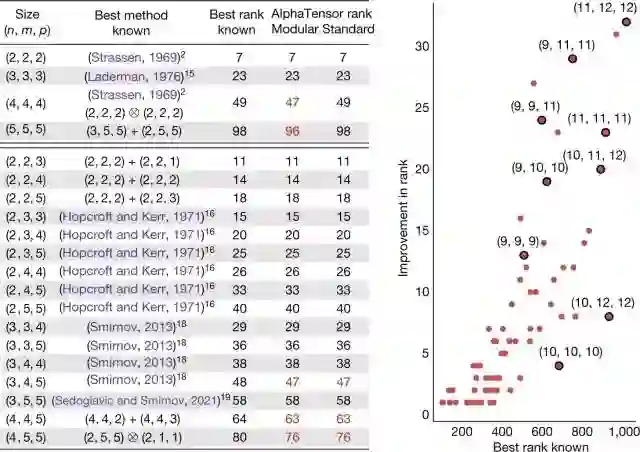
例如，如果学校里教的传统算法是用100次乘法对一个4x5乘以5x5的矩阵进行乘法，而这个数字在人类的聪明才智下被减少到80次，AlphaTensor已经找到了只用76次乘法就能完成同样操作的算法。

 

 

 

除此之外，AlphaTensor的算法自50年前发现以来，首次在有限域中改进了Strassen的两级算法。这些小矩阵的乘法算法可以作为基元来乘以任意大小的大得多的矩阵。

 

此外，AlphaTensor还发现了一组具有最先进复杂度的多样化算法--每种大小的矩阵乘法算法多达数千种，表明矩阵乘法算法的空间比以前想象的要丰富。

 

在这个丰富的空间中的算法具有不同的数学和实践属性。利用这种多样性，我们对AlphaTensor进行了调整，以专门寻找在特定硬件上速度快的算法，如Nvidia V100 GPU，和谷歌TPU v2。

 

这些算法在相同的硬件上比常用的算法 快10-20% ，这展示了AlphaTensor在优化任意目标上的灵活性。

 

 

 

AlphaTensor的目标是对应于算法的运行时间。当发现一个正确的矩阵乘法算法时，会在目标硬件上进行基准测试，然后反馈给AlphaTensor，以便在目标硬件上学习更有效的算法。

未来的研究和应用

从数学的角度来看，我们的结果可以指导复杂性理论的进一步研究，其目的是确定解决计算问题的最快算法。

 

通过以比以前的方法更有效的方式探索可能的算法空间，AlphaTensor有助于推进我们对矩阵乘法算法的丰富性的理解。了解这个空间可能会释放出新的结果，帮助确定矩阵乘法的渐进复杂性，这是计算机科学中最基本的开放问题之一。

 

因为矩阵乘法是许多计算任务的核心组成部分，涵盖了计算机图形、数字通信、神经网络训练和科学计算，AlphaTensor发现的算法可以使这些领域的计算效率大大提升。

 

AlphaTensor网络架构

 

AlphaTensor在考虑任何类型的目标方面的灵活性也可以刺激新的应用，以设计优化能源使用和数值稳定性等指标的算法，帮助防止小的四舍五入错误随着算法的工作而滚雪球。

 

虽然我们在这里集中讨论了矩阵乘法这一特殊问题，但我们希望我们的论文能够启发其他人使用人工智能来指导其他基本计算任务的算法发现。

 

我们的研究还表明，AlphaZero是一个强大的算法，可以远远超出传统游戏的领域，帮助解决数学中的开放问题。

 

在我们的研究基础上，我们希望能够推动更多的工作--应用人工智能来帮助社会解决数学和整个科学领域的一些最重要的挑战。

参考资料：

https://www.nature.com/articles/s41586-022-05172-4

https://www.newscientist.com/article/2340343-deepmind-ai-finds-new-way-to-multiply-numbers-and-speed-up-computers/

——END——