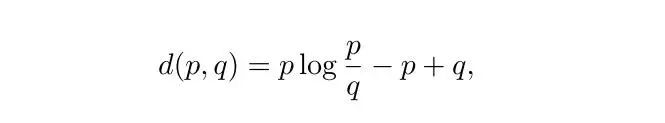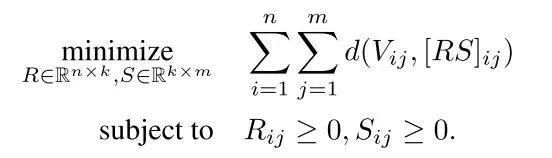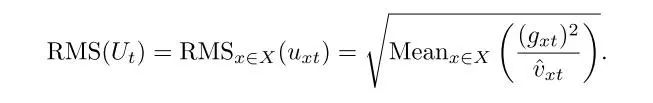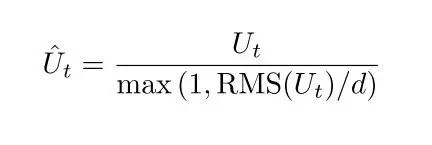谷歌提出最新参数优化方法Adafactor，已在TensorFlow中开源

2018 年 4 月 29 日 AI前线 紧跟前沿的

策划编辑 | Natalie

编译 | 郝毅

编辑 | Emily

AI 前线导读：在深度学习训练过程中，需要对大量参数进行优化，目前主流的优化方法主要有 SGD、Adam、RMSProp 等。尽管这些方法已经被广泛的使用，但在许多方面仍需改进。近日，谷歌团队提出一种新的优化方法 Adafactor，针对目前主流优化方法存在的问题进行改进，对比其他优化算法在机器翻译任务上取了的目前最好的结果。本文对这一成果进行了解读，这是 AI 前线的第 29 篇论文导读。

更多干货内容请关注微信公众号“AI 前线”，（ID：ai-front）

简介

深度学习的训练过程需要优化大量的参数，基于梯度的优化方法是目前用于训练深度神经网络的主要方法。例如最简单的随机梯度下降算法 (SGD)，SGD 就是在一个 minibatch 内让参数沿着损失函数的负梯度方向走一定的步长。在这个基础之上，许多基于梯度的自适应方法应运而生，例如使用累计平方梯度的 Adagra、使用指数平均的 RMSProp 方法、使用自适应矩估计的 Adam 算法以及 Adadelta 等。

在使用大量参数训练神经网络时，假设我们的计算资源是一定量的，如果训练过程能够占用更少的内存，则可以使用更加复杂的模型进行训练，这样模型就能获得更好的效果，也就是内存的用量直接决定了模型的大小。而上述优化算法在带来更好性能的同时，也需要大量的内存进行计算，尤其是自适应优化算法需要更多的内存来保存额外的参数。例如 Adam 算法对于每一个参数都需要额外两个指数衰减值，造成了三倍的内存消耗。此外，自适应算法参数更新的时容易出现迭代过程不稳定的情况。

本文从内存消耗、参数更新以及迭代步长三个方面对 Adam 算法进行了改进，并与 Adam 方法在大型机器翻译任务上进行了比较，Adafactor 在使用更少内存的同时获得了更好的效果。

Adam 算法的回顾

Adam 这个名字来源于 adaptive moment estimation，自适应矩估计。概率论中矩的含义是：如果一个随机变量 X 服从某个分布，X 的一阶矩是 E(X)，也就是样本平均值，X 的二阶矩就是 E(X^2)，也就是样本平方的平均值。Adam 算法根据损失函数对每个参数的梯度的一阶矩估计和二阶矩估计动态调整针对于每个参数的学习速率。

Adam 也是基于梯度下降的方法，但是每次迭代参数的学习步长都有一个确定的范围，不会因为很大的梯度导致很大的学习步长，参数的值比较稳定。下面是 Adam 算法的伪代码：

Adam 算法的每部迭代过程主要是以下两步骤：

从训练集中随机抽取一些样本以及相关输出
计算梯度和误差，更新 mt 和 vt 以及梯度，并计算参数更新。

步长一般设置为常量，但是近期一些工作认为使用线性衰减的方法设置步长可以得到更好的优化效果。本篇论文中，作者使用倒数平方根衰减获得更稳定的结果与 Adafactor 方法进行了对比。

内存消耗

使用低秩分解

在深度学习方面，普遍存在一个“潜规则”，那就是更大的模型往往能带来更好的效果。例如语言模型和机器翻译任务，甚至在一些政治模型也有数十亿的参数。优化方法使用的额外参数就会带来严重的内存占用问题。

处理一个大型矩阵的时候，我们习惯使用低秩毕竟的方法替换这个大型的矩阵来解决一些运算上的问题。比如最广为人知的低秩逼近方法——奇异值分解 (SVD)。本文的作者为了寻求更合适的方法，从非负矩阵分解中寻找灵感。除了 F 范数外，另一种比较常用的代价函数是 K-L 散度，也被称为 I- 散度。对于非负的标量输入，I- 散度可以表示为下式：

使用该代价函数，我们可以最小化所有的元素级散度，让它们服从部件级非负约束：

对于上面这个方程组，我们无法直接获得 k 阶分解，但是在一阶分解时，可以求得其解析解。然后利用一阶解的性质对模型参数进行优化，算法过程如下：

类似 Adafactor 的方法最早是由 Hinton 团队在论文 2017 年 ICLR 的论文”Outrageously large neural networks: The sparsely-gated mixture-of-experts layer”提出。在 2014 年，Gupta 团队使用嵌入向量的方法对 Adagrad 的累积项进行平均，同样实现了减少内存的使用。在性能相同的情况下，Adafactor 可以将内存的占用从 O(nm) 减小到 O(n+m)。

删除动量项

在 Adam 算法中，每个参数都需要两个额外的累计项。上面的算法对第二个累积项进行了分解，减少了其内存占用。为了移除第一个累积项，作者首先尝试了直接将 beta1 设置为 0。

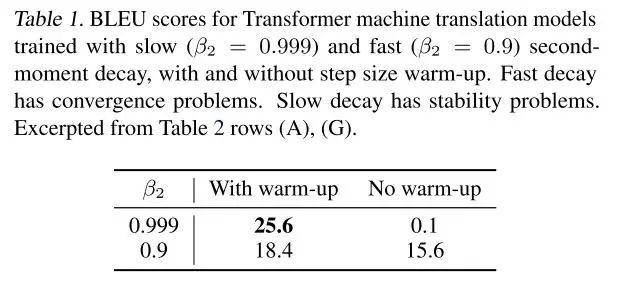
通过实验结果可以看出，在没有 warmup 的情况下，没有动量的优化算法会很不稳定，下图是实验结果的对比。BLEU 是机器翻译领域的一种评价准则，全称是 Bilingual Evaluation Understudy，简单的理解就是分数越高表示翻译结果越接近正确的人工翻译结果。

参数更新

使用整流的方法约束更新

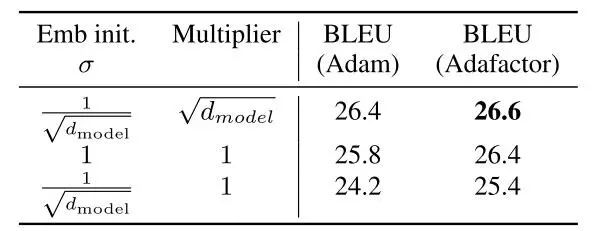
Reddi 团队的文章“On the convergence of adam and beyond. International Confer- ence on Learning Representations”谈到了 Adam 算法中使用快速的二阶矩估计衰减 (即 beta2 设置的较低) 会导致不收敛的问题。本文的作者在实验中也发现了这个问题，并且较慢的衰减 (即较高的 beta2) 会导致训练的不稳定，有无预训练过程对结果影响很大，实验结果见下表：

对于这一现象，作者是这样解释的：较慢的衰减速率意味着二阶矩估计是基于更早的梯度的原因。如果模型优化的很快，就会导致很高的估计误差，这就导致了参数更新时候产生的错误。本文中，作者使用了均方根值来检测模型的训练过程中是否出现了这个问题。

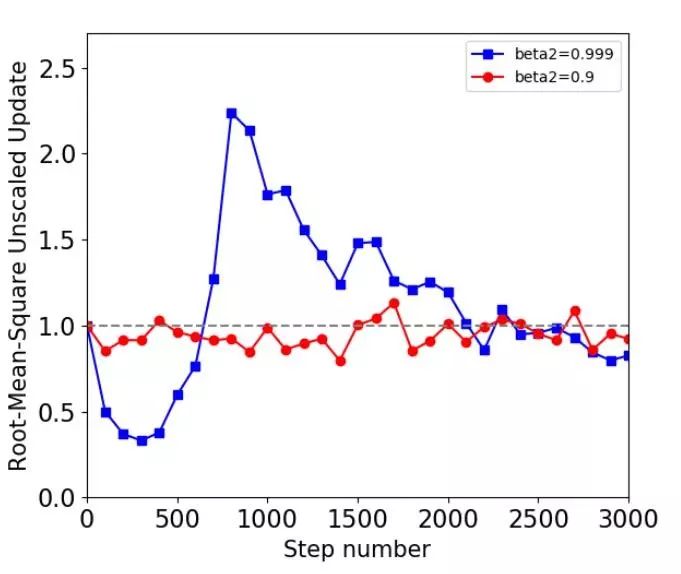
作者绘制了 RMS 曲线来说明训练过程中不同的衰减对训练效果的影响。从下图可以看出，beta 设置为 0.999 时，RMS 值时大时小，训练过程不稳定，这就是由过时的二阶矩估计导致的。

为了避免过时的二阶矩估计带来的参数更新，作者使用了一种整流的方法对更新值进行修正，对于超过设定阈值的更新，会等比例的进行缩小，函数如下：

在以往的研究中，有许多直接修正梯度的方法。但是对于 SGD 方法，函数的下降方向就是负梯度方向，所以直接修正梯度会对训练过程造成负面影响。同样，在许多自适应方法中使用这种做法，标准化的更新方向仍然会超过用户设置的阈值，这是由于每个参数都有额外的缩放因子。在本文中，作者对需要更新的参数本身进行标准化而不是只使用梯度。

增加衰减参数

本文的作者受“On the convergence of adam and beyond. International Confer- ence on Learning Representations”一文启发，使用逐渐增加衰减的方法修改 beta1 和 beta2，具体算法如下：

使用该算法后，beta2 在 t=1 的时刻为 0，然后逐渐趋向于设定的 beta2 的值。除此之外作者还提出了其他的具体算法实现衰减的逐渐增加。

迭代步长

不同于传统的固定步长的方法，本文提出了一种相对步长的策略。针对向量形式的权重和矩阵形式的权重分别有不同的优化方法，实验证明使用相对步长优化算法可以获得更好的表现，下面是算法的实验结果。

Adafactor 算法

结合上述三条策略，完整的 Adafactor 算法如下所示，其中，算法 4 是针对矩阵形式的参数设计的优化算法，算法 5 则是为向量形式的参数所设计。值得一提的是 Adafactor 算法已经在最新的 TensorFlow 中开源，用户可以通过 TensorFlow 的 optimize 直接调用 Adafactor，源码地址：

https://github.com/tensorflow/tensor2tensor/blob/80b2f7300ce2021b9ca0a7877b2670bbdea2b2bf/tensor2tensor/utils/optimize.py