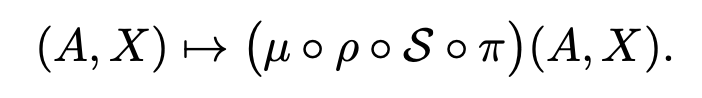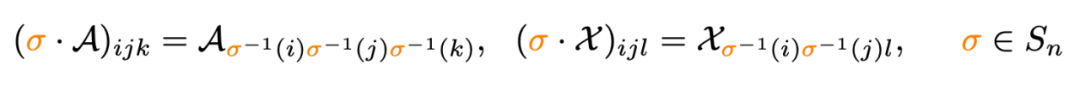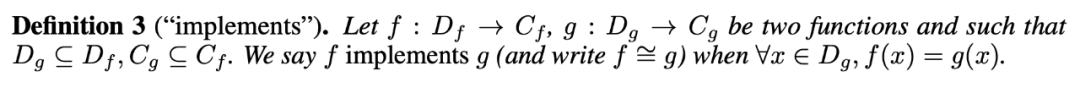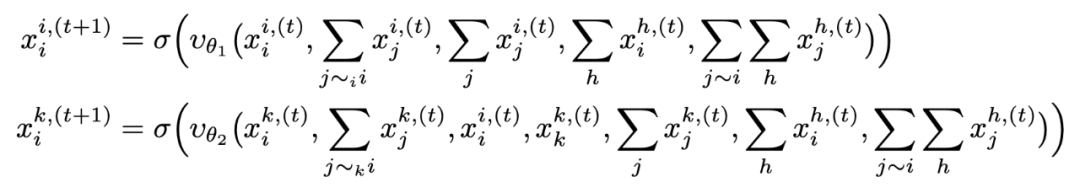NeurIPS 2022 | 利用子图和结点的对称性提升子图GNN

来源： PaperWeekly

本文约1100字，建议阅读5分钟
本文测试了当采取训练数据的一小部分时，模型能否仍有效，即模型的泛化能力如何。

1、论文介绍

子图 GNN 能够将图建模成为子图的集合。时至今日，对于子图 GNN 结构的设计和其性质的理论分析方向仍有待探索。本文研究了子图方法中最重要的部分——基于结点的子图选择策略，如 ego-network/node marketing/node deletion。本文将子图表达能力的上界界定为 3-WL，并设计了新的子图 GNN 模型，称之为 SUN，在理论上统一了之前的子图模型，并在多个数据集上取得了更优越的表现。

2、动机

目前已有许多工作，旨在提升 GNN 的表达性。其中另辟蹊径在子图领域进行的研究也不在少数。这些方法通常是从原始输入图中提取出子图集 (bags)，并在子图集上进行聚合等一系列操作，目的是对原图进行有效的表示。 

从原图中挑选并提取子图有许多策略，选择不同的策略对模型的时间开销和性能表现存在影响。

尽管子图 GNN 拥有广阔的发展前景，我们仍缺少对其系统理解与理论分析。首先，理论上子图方法能够严格超越 WL test，但其 expressive power 的上界仍未可知。其次，在实践上，各种模型之间采取的信息传递和聚合策略是有差别的，是否存在对于信息传递规则的一个通用理解？在这两方面之上，我们既需要对于各种模型表达能力上界进行合理的标定，又希望能够在之后设计出更强大的子图 GNN。 

基于以上，本文提出并解决了两个问题：1）这些子图 GNN 方法的表达能力上界在哪里；2）在子图集上进行的等变信息传递层之间的内在联系是什么。 

本文的贡献主要有以下两点：

1. 对在子图集上进行操作的对称性集合提出了新的分析；

2. 提出了 SUN，对之前基于结点的子图 GNN 进行了合理的泛化。

3、方法

3.1 Subgraph GNNs

子图 GNN 按如下公式计算图 G 的表示：

其中，

 是从图 G 生成子图集的子图选择策略。 是对结点和子图进行排列组合的 T 个等变层；  是具有不变性的池化函数。  是 MLP；不同的子图 GNN 区别在于采取不同的   和  。

一个基于结点的子图选择策略表示为  ，输入是一张图 G 和一个结点 v。

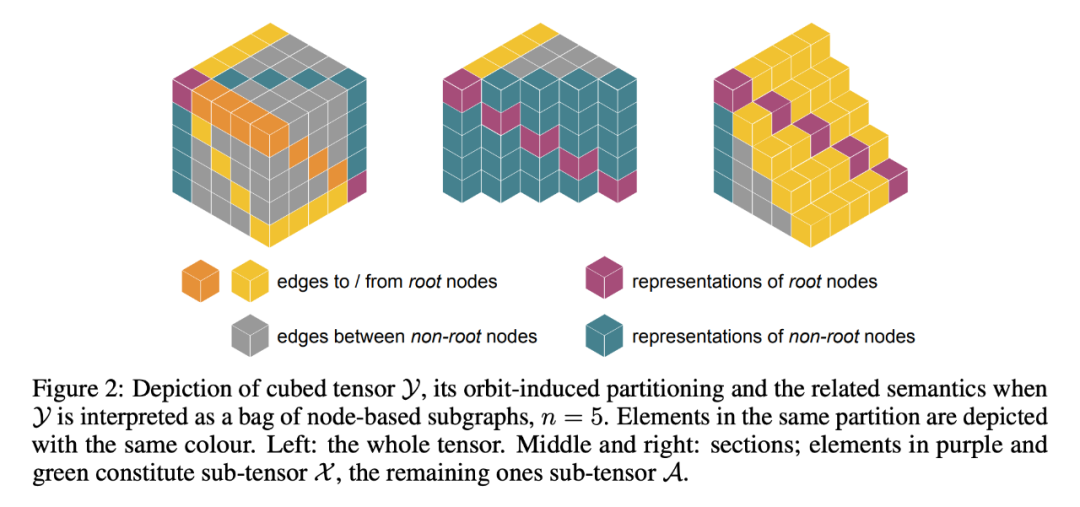
3.2 基于结点的子图选择策略的symmetries

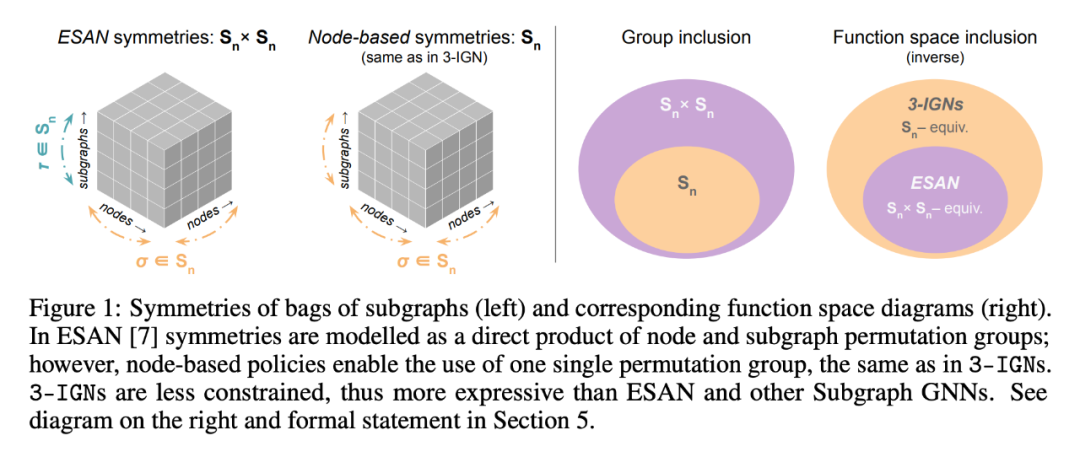
以往的工作对子图集采取两套排列组合方式：在结点上进行的   和在子图集上进行的  。

本文观察到，当采用基于结点的选择策略时，子图和结点之间存在一种对应关系，因此本文仅仅采用单个排列组合   同时应用于结点和子图上：

3.3 SubGNNs的上界

在本节中，本文证明了子图 GNN 的上界是 3-WL，原因是能被 3-IGN “inplement”：

3.4 A design space for subGNNs

3.5 SUN

4、实验

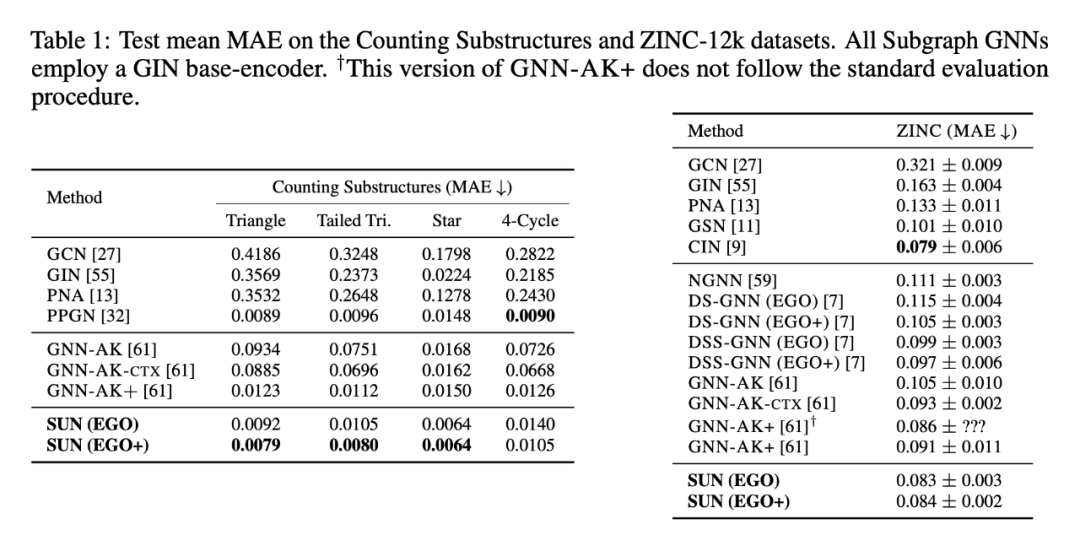
人工数据集上的任务是对图中子结构进行计数，SUN 在 4 个任务中的 3 个上表现都最好；真实数据集采用 ZINC-12k，用 MAE 进行衡量，SUN 取得了 SOTA 的结果。

本文测试了当采取训练数据的一小部分时，模型能否仍有效，即模型的泛化能力如何。

5、总结

本文的工作对现有子图 GNN 的工作进行了统一和拓展，并界定了这些方法的 expressive power 上界是 3-WL。通过对 expressive power 在 1 & 3-WL 之间的模型进行系统研究，提出了子图 GNN 这一类模型的通用理论。在实验部分，本文额外研究了这些模型的泛化能力，其中 SUN 表现最好。

论文标题：

Understanding and Extending Subgraph GNNs by Rethinking Their Symmetries

论文链接：

http://arxiv.org/abs/2206.11140

代码链接：

https://github.com/beabevi/SUN