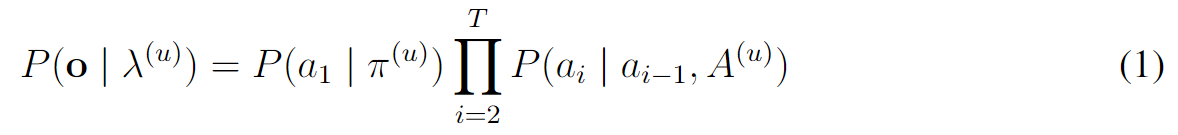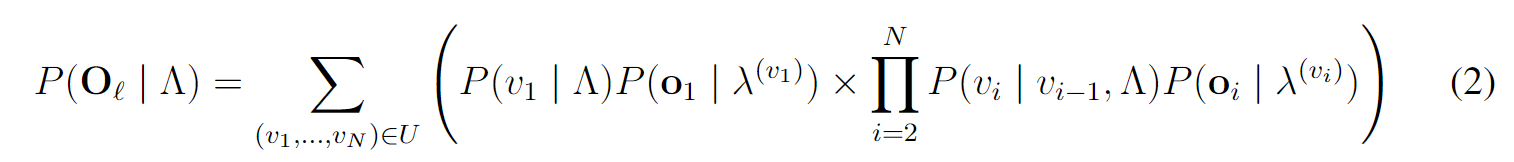论文笔记 | Modeling MOOC Student Behavior

Journal of EDM 2017

链接：http://jedm.educationaldatamining.org/index.php/JEDM/article/view/211/pdf_33

一、背景简介

1、研究背景：MOOC平台记录了学生的学习行为日志，通过行为建模可以分析学生的学习趋势、学习状态、学习习惯等等，基于此，教学者可以做出相对应的改变来影响学生的学习效果。然而，目前对学习行为建模的许多工作仅仅只是“表层的”，例如对学生的各种行为进行统计，设计一些启发式规则挖掘显著的行为模式等等。因此，希望能够通过分析行为模式之间的关系，更好地去理解学生。

2、研究问题：利用无监督学习对学生行为进行建模，自动抽取出可解释的行为模式，不仅仅是去估计学生在不同状态下各种行为的分布，更是这些行为之间、行为模式之间的关系

3、相关工作：隐马尔可夫模型（HMM）及其应用（speech recognition、part-of-speech tagging、econometrics）；HMM在结构上的扩展以及一些代表工作（multi-layered HMM、Hierarchical HMM、Mixtures of HMM）；HMM在MOOC上的一些应用（行为聚类、学习策略转移、知识跟踪、行为模式预测）

4、动机和思路：1）学生的行为比较复杂，这里考虑用隐状态来表示学生的行为模式，而不是预先用一些规则去定义；2）学生行为是随时间变化的，将每一个学生直接扁平化成特征向量会丢失很多信息，因此这里保留数据的序列化结构，并通过状态的转移概率来对动态行为建模；3）应当允许不同时间粒度上的行为分析，粗粒度上反映的是学习目标的转移，细粒度上反映的是单个行为的转移。

二、算法模型

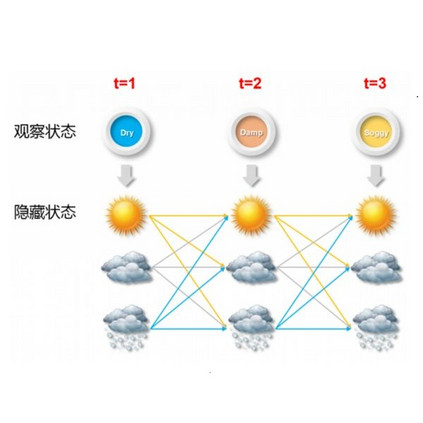
1、HMM的思路：最简单、直接的想法是，把行为看成是可观察的output，隐状态是行为模式，那么隐状态是行为的概率分布，会缺失行为之间的转移关系。因此，这里的2L-HMM加入了行为之间的依赖关系，在隐状态表示行为模式的基础上，通过将一个session看成是一个output，对这个session再用Markov Model学一个转移概率矩阵。

2、形式化定义：（1）第一层的Markov，对于K个状态，每个状态有一个初始概率分布和转移概率矩阵；（2）第二层的HMM，有隐状态的初始概率，转移概率矩阵，以及第一层的K组参数（不需要发射矩阵了）

3、参数估计：EM算法（Baum-Welch）

三、实验结果

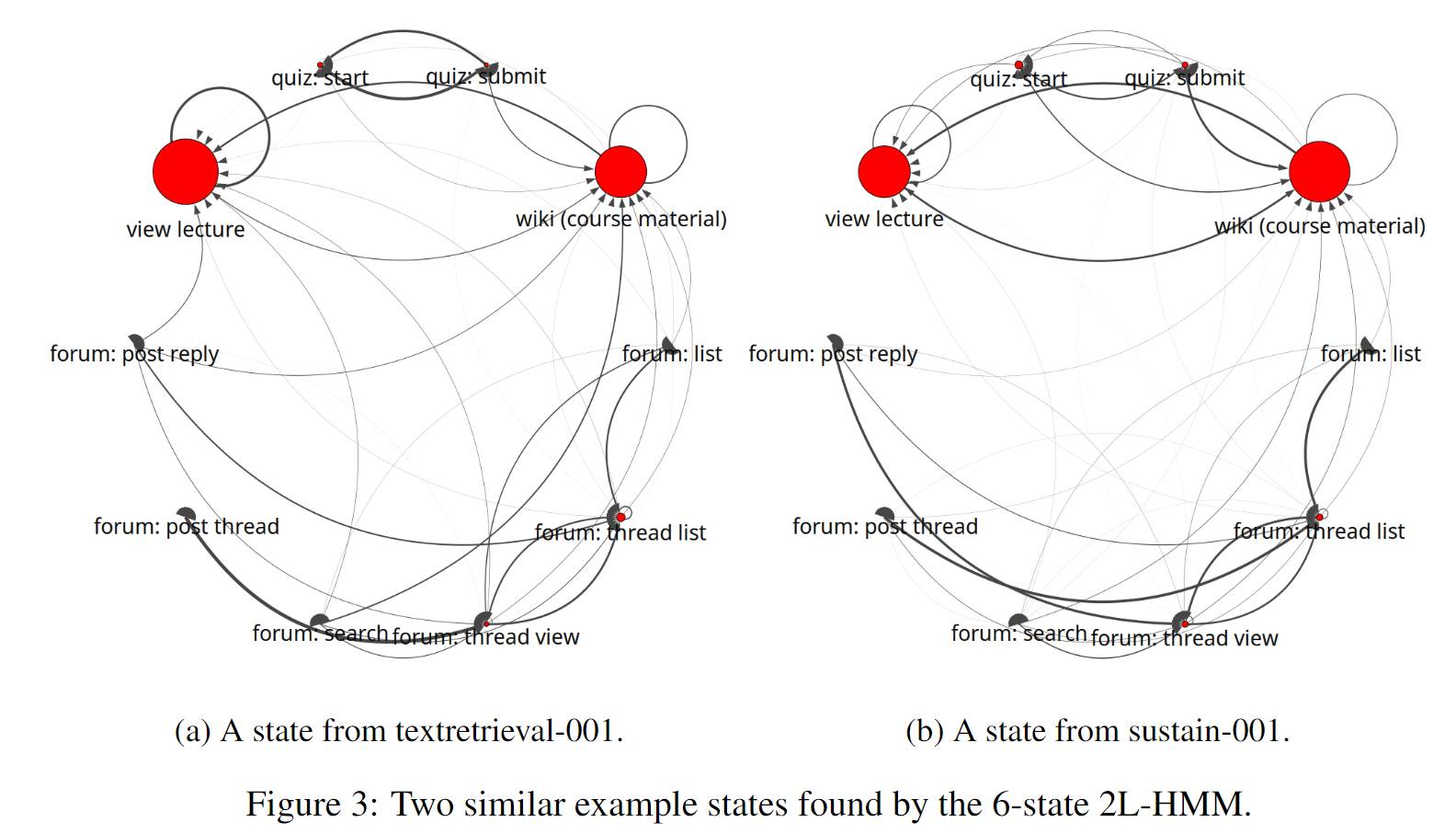
1、隐状态的效果展示：点的大小是单个行为的Pagerank值，反映出这种行为模式的主要行为，边的粗细是转移概率，反映这种模式下行为之间的关系。作者对比了不同隐状态的点和边，以及不同课程的相似的隐状态。

2、隐状态的个数：从2变到4，能够分离出一些特殊的行为模式，但随着状态数再往上增加，可能分离出的状态会很相似或解释不了。

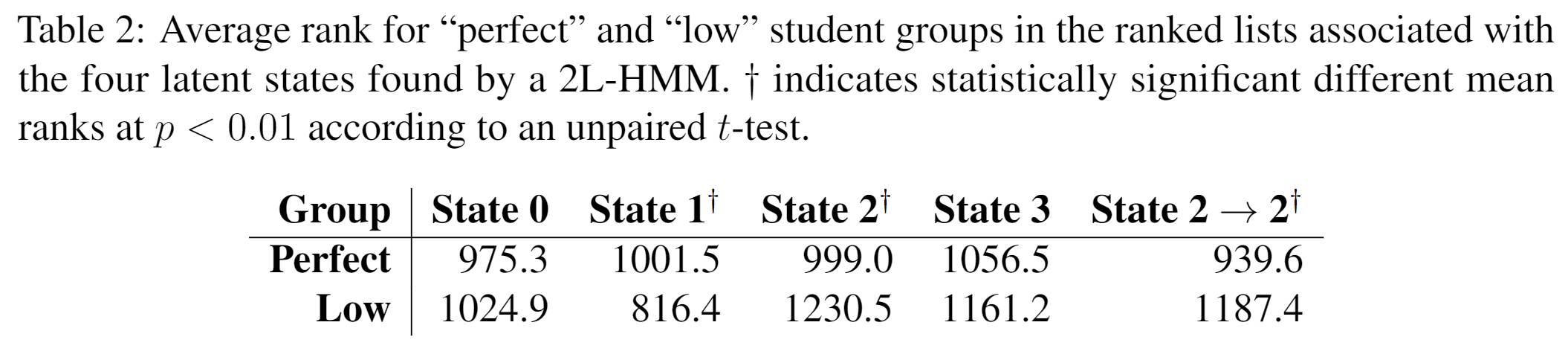
3、隐状态之间的转移：文章考察了不同状态以及状态转移概率对学生学习成绩的相关性分析。

四、思考

1、如文中所述，模型存在一些缺陷，如：需要预先定义参数、没有考虑session内的状态转移、某些行为模式的缺失

2、隐状态的含义需要转移（文章中的隐状态其实是一个状态转移概率矩阵，以及衍生出的PageRank值，需要理解行为之间的关系之后才好去定义含义）

3、能够解决什么实际问题？（HMM其实是一个生成模型，能够比较好地反映出数据的分布，因此这里主要是对模型结果的展示，没有模型效果上的分析说明）

作者：朱纪乐，北京大学在读硕士，研究方向为教育数据挖掘、推荐系统