征文 | 混沌（Chaos）世界——无序中的数学之美

会员服务 ·

征文 | 混沌（Chaos）世界——无序中的数学之美

2019 年 7 月 6 日 遇见数学

本文参与遇见数学＃数学蒲公英＃第一次征文活动，作者张瀚升，10岁，2009年6月28日出生，山西省太原市万柏林区现代双语小学四年二班。

为什么相同的细胞会组成不同的组织？

为什么相同的原子会组成不同的元素？

为什么河流、血管、树枝都具有类似的结构？

为什么数学方程可以画出各种绚丽的图案？

为什么数学的研究对象如此优雅美丽？

为什么很多美丽源自混沌？

......

我的脑子里总是有着这样那样的疑问，总是想去一探究竟，于是，我在各种各样的书籍中寻找着答案，却发现，在数学里，总有一个或简单或复杂，但是却让你越来越有兴趣去发现的快乐与惊喜的源泉，就像现在，我将带你们走近一个完全不同的混沌世界，一起看看这些科学界无法解释的种种谜团。

说到这里，我们必须要先解开最核心的一个谜题：什么是混沌？它既不是吴承恩笔下《西游记》描述的“混沌未分天地乱，茫茫渺渺无人见”的一番冷清景象，也不是盘古开天辟地之后的混乱展现，更不是希腊神话中的洪水和深深的黑暗；它，其实是一个可以被数学公式所解释的系统，是数学之美的基础，是随处可见却又鲜为人知的系统。

混沌，是由阿兰·图灵（Alan Turing 1912-1953）最早触及。他是一个破译密码的高手，所以才能破译大自然这般神奇却又复杂的终极密码。

现在，我们来看第一个问题：为什么相同的细胞会形成不同的组织？这是一个被称为“形态发生”的过程，非常令人费解，它的另一个名称是“自组织”，可以用一个很简单的数学公式来描述。最初，胚胎内的细胞都是完全相同的，可是经过细胞的一次次聚集，一次次分化，实现了“自组织”，变成各种各样的细胞和组织，这也正是沙粒的形态基本相同，沙丘形态各不相同，奶牛、斑马等动物身上颜色不一样的原因之一。

细胞分裂(图自 pixabay)

我们再看第二个问题：为什么相同的原子会形成不同的元素？其实，这个问题和上一个问题本质相似，也是“自组织”的一个鲜明例子。原子和质子、电子一开始也是不变的，之后开始聚集、分化，但是它们自身不变，只不过它们合成元素的原子数量不同，排序方式不同而已。

现在，第三个问题应该可以解释了：为什么河流、血管、树枝都具有相似的结构？这需要涉及到与混沌紧密相关的另一个名词——分形（Fractal）。

说到分形，就不得不提到一个人，一个图形——法国数学家伯努瓦·曼德博和他的曼德博集合（Mandelbrot Set）。

让我们一起看一看20世纪数学皇冠上最闪耀的宝石：曼德博集合，被誉为“上帝的指纹”，不仅仅是人类有史以来做出的最奇异,最瑰丽的几何图形，也不仅仅是最具代表性的分形图案，更是一个由及其简单的数学规则诞生的几何奇迹。

上帝的指纹 - 曼德博集合(图自维基)

最让人觉得不可思议的是，曼德博集合的定义令人难以置信的简单，这个图形仅仅是一些数列的基本性质的几何标识：

曼德博集合是复二次多项式

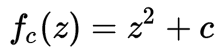
进行迭代来生成。其中，c 是一个复参数。对于每一个 c，从 z = 0 开始对 f(z) 进行迭代。

序列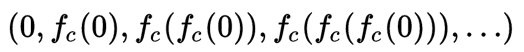的值或者延伸到无限大，或者只停留在有限半径的圆盘内（这与不同的参数c有关）。

曼德博集合就是使以上序列不延伸至无限大的所有 c 点的集合，所有使得无限迭代后的结果能保持有限数值的复数 c 的集合，构成曼德勃罗集，每个输出值成为下一次运算的输入值，就像循环播放的视频一样，达成自然界基本的有序。

那么，究竟什么是分形呢？分形是由曼德博提出的，也叫做自相似的定理，是指相同形状在越来越小的尺度上一直重复的现象，比如支气管、树枝、河流等，它们会无限地重复下去......

图自www.researchgate.net

现在，我们再来解答这个问题：为什么很多美丽源自混沌？可能很多人都会认为：美丽和混沌这两个词连边都不沾，的确，字典中这两个词的意思几乎完全相反，但是，事实真的是这样子的吗？不！不是，所有数学的美，都可以用混沌来描绘出来，它们或波澜壮阔，或幽静神秘，每一幅都比画家用画笔创作的图画要美丽许多。

在这里，我想说一下大家都很熟悉的现象——蝴蝶效应，指某种东西的微小变化越演越大且形成无法预测，无法阻止，无法改变的效应，这使很多东西不能达到人们预期的效果，很多科学定律也因此崩溃。而图灵的模式（pattern）,别洛乌索夫反应和他的分形，全部指向一个最基本的深藏的宇宙法则：简单的规则可以自然地导致复杂事物的发生。