数学中的“大统一理论” | 2018 年阿贝尔奖

2018 年 3 月 22 日 科研圈

3月20日，罗伯特·朗兰兹被授予 2018 年度阿贝尔奖——数学界的最高荣誉之一，以表彰他提出了连接表示论和数论的极具远见的纲领。他所提出来的“朗兰兹纲领”试图构建数学中的“大统一理论”，这是一代代数学家所追求的目标。（获得 2018 年数学新视野奖的年轻中国数学家张伟和恽之玮的工作也是受到朗兰兹哲学的启发。）

现年 81 岁的朗兰兹是普林斯顿高等研究院的荣誉退休教授，他所提出的朗兰兹纲领探讨的是现代数学中的两大支柱——数论与调和分析——之间的深层联系。数论研究的数字之间的算法关系，被认为是“最纯”的数学领域；调和分析也是数学的一个分支，它是从微积分中发展出来的。在他之前，这两个领域被认为是毫无关联的，而它们之间的联系其实有着深远的影响，被数学家用来解答与质数性质有关的问题。

朗兰兹在数论和调和分析的深刻洞见包括提出了自守形式和代数数论的一般性原则，引进了 L-函数的一般类，构建了艾森斯坦级数的理论，提出了解决阿廷猜想的特定情况的技巧，引进了“内窥”（Endoscopy），以及发展了联系志村簇的 ζ 函数和自守 L-函数的技巧。

2016年，罗伯特·朗兰兹出席了普林斯顿高等研究院举办的一次关于“超越内窥”的会议。（图片来源：Dan Komoda/Institute for Advanced Study）

1967 年，朗兰兹首次阐述了这一构想，当时年仅 30 岁的朗兰兹在一封写给著名数学家安德烈·韦伊（André Weil）的信中提到了这一计划，这是一个思考数学的全新方式。在这封 17 页长的信中，他谦和的写道：“如果您愿意把它看作是纯粹的推测，我会很感激；如果不愿意，我相信您身边就有一个废纸篓。”

从那时起，一代又一代的数学家开始接受并扩展了他的构想。现在，朗兰兹纲领所涵盖的领域非常多，因此通常被认为是数学界的“大统一理论”。就数学史而言，这可以说是革命性的。

数学家一直想要找寻质数的规律。质数就像是数论的原子元素，是算法研究的基础。它们的数量是无限的，但它们的分布却似乎是随机地散落在数字中。为了找到质数中的规律，比如它们出现的频率（即著名的黎曼假设的主题），数学家必须将它们与其他事物联系起来。准确说来，质数就像一个密码，当你找到正确的阅读密钥时，它就变成了令人愉悦的信息。

质数看起来非常随机，但通过朗兰兹纲领，就会发现它们有着一个非常复杂的结构，能够与各种其他事物联系起来。有一个与质数结构相关的问题是——哪些质数能用两个质数的平方和表示，例如：

质数 5 = 2²+1²

质数 13 = 3² + 2²

质数 29 = 5² + 2²

在 17 世纪，数论学家发现，所有能用两个质数的平方和表示的质数都有一个共同性质——当它们除以 4 时，余 1。这一发现揭示了质数的一种隐藏结构。到了 18 世纪末期，数学家高斯（Carl Friedrich Gauss）对这一奇妙的关联进行了概括，它的“互反律”用公式将那些等于两个质数的平方和的质数，与除以 4 余 1 这个特征联系了起来。

在朗兰兹的信中，他在高斯发现的互反律基础上，提出了更广泛的延伸。高斯的定律适用于指数不高于 2 的二次方程。但朗兰兹认为，在三次、四次等高阶方程中产生的质数，应该与调和分析成互反关系。

调和分析被频繁的运用于物理问题的解决。例如在 19 世纪，科学家惊奇地发现，当通过棱镜观察星光时，并没有观测到连续的光谱。相反，光谱会被出现在各处的黑线所中断，我们现在称这些黑线为吸收光谱。后来科学家们终于意识到，失踪的光线是被恒星中的元素所吸收。于是这一发现为证明恒星与地球是由相同的材料构成提供了强有力的证据。

与此同时，光谱线也成为具有数学意义的存在。缺失的那些光波给出了一系列失踪光频的数字。数学家可以通过分析来研究这些数字；或者，他们还可以用从物理学问题中得到的启发，但又纯粹源自于分析和几何学中发展出的全新方程式来进行研究。基于这些新的方程，他们可以研究吸收光谱的一种并行概念。

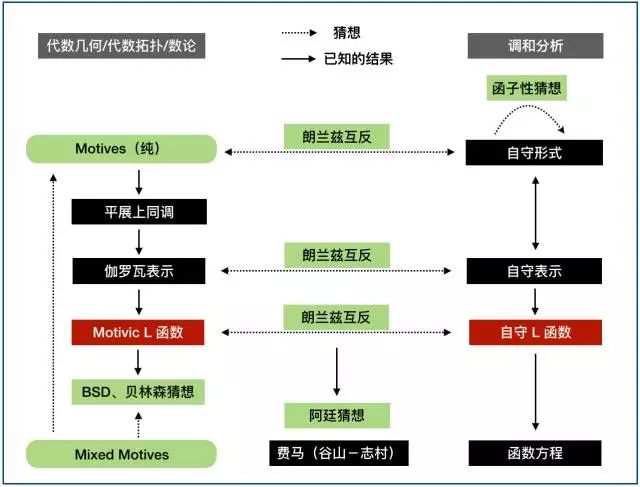
朗兰兹纲领就将多项式方程的质数值与分析和几何学中研究的微分方程的谱相联系到一起，并认为这两者之间应该存在互反关系。因此，我们应该能通过了解哪些数字出现在相应的光谱中，来表示哪些质数出现在特定的情况中。

不过这两组数字不能被直接比较，它们必须都通过不同的数学对象进行翻译。具体而言，基于质数的伽罗瓦表示法应该与包含相关光谱的自守形式配对。

如今，研究朗兰兹纲领的数学家正试图证明这种关系以及其他许多相关的猜想。与此同时，他们正在用朗兰兹型的联系来解决那些本看似遥不可及的问题。其中最著名的成果是数学家安德鲁·怀尔斯（Andrew Wiles）在上世纪 90 年代初对费马大定理的证明。怀尔斯的证明部分取决于朗兰兹早在几十年前就预言过的数论和分析之间的关系。