双“11”搞促销？用贪心算法盘它

作者 | 王磊

来源 | Java中文社群（ID：javacn666）

头图 |  CSDN 下载自东方IC

这几年商家为了刺激消费是变着花样的推出各种各样的活动，以某多多为首的运营式电商更是让我们看到了营销的无限“潜力”。

这不，最近刚赶上双 11，小区便利店的老王头也推出了一项「空酒瓶子换酒」的促销活动，它的规则是这样的。

本文已收录至 Github《小白学算法》系列：https://github.com/vipstone/algorithm

活动规则

客户购买 X 瓶酒，就可以用 Y 个空酒瓶来兑换一瓶新酒。

提示：

X 和 Y 的取值如下：

• 1 <= X <= 100
• 2 <= Y <= 100

Y 值不固定，随机抽取。

如果喝掉了酒瓶中的酒，那么酒瓶就会变成空的。

请你计算最多能喝到多少瓶酒。

示例 1：

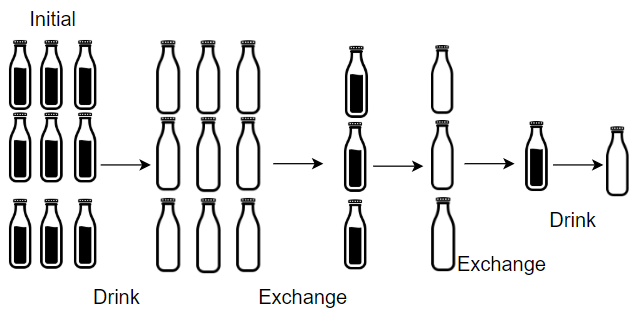
输入：X = 9, Y = 3

输出：13

解释：你可以用 3 个空酒瓶兑换 1 瓶酒。所以最多能喝到 9 + 3 + 1 = 13 瓶酒。

示例 2：

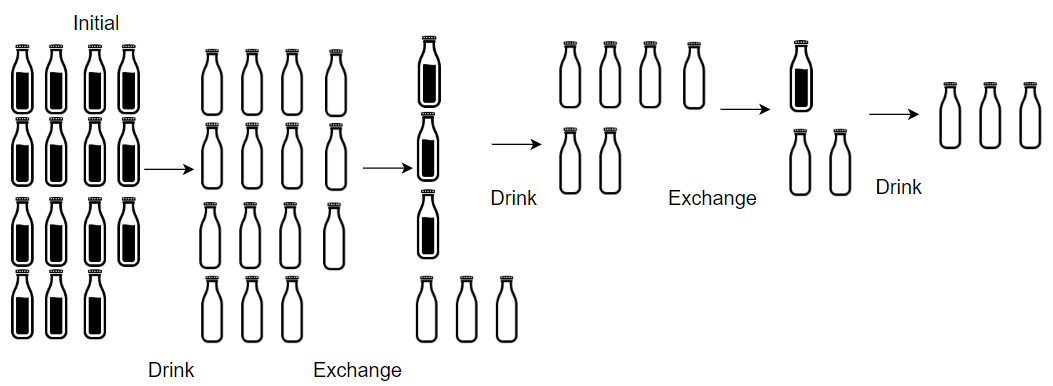
输入：X = 15, Y = 4

输出：19

解释：你可以用 4 个空酒瓶兑换 1 瓶酒。所以最多能喝到 15 + 3 + 1 = 19 瓶酒。

示例 3：

输入：X = 5, Y = 5

输出：6

示例 4：

输入：X = 2, Y = 3

输出：2

解题思路

这道题难点有两个：第一，用多少个空瓶换一瓶酒是不固定的（随机的）；第二，兑换的酒喝完之后还能继续参与兑换活动。因此要在满足这两个的前提条件下，计算自己最多能喝到几瓶。

可能有些朋友看到了本篇标题之后就知道了解题思路，没错，我们本文就是要用「贪心算法」来计算最终答案。同时这道题也符合贪心算法的解题思路，那就是有酒瓶就兑换、能兑换多少就兑换多少。

贪心算法

贪心算法（Greedy Algorithm），又称贪婪算法，是一种在每一步选择中都采取在当前状态下最好或最优（即最有利）的选择，从而希望导致结果是最好或最优的算法。

贪心算法在有最优子结构的问题中尤为有效。最优子结构的意思是局部最优解能决定全局最优解。简单地说，问题能够分解成子问题来解决，子问题的最优解能递推到最终问题的最优解。

贪心算法的实现框架

从问题的初始解出发：

while（能朝给定总目标前进一步）{    利用可行的决策，求出一个可行解元素；}由所有解元素组合成问题的一个可行解。

注意：因为用贪心算法只能通过解局部最优解的策略来达到全局最优解，因此，一定要注意判断问题是否适合采用贪心算法策略，找到的解是否一定是问题的最优解。

接下来我们就用代码来演示一下贪心算法的具体实现。

代码实现 1：贪心

首先我们先把全局问题转换成局部问题：当空瓶子能换一瓶酒的时候，我们就换一瓶酒，实现代码如下：

// 贪心1：用 + 和 - 实现class Solution {    public int numWaterBottles(int numBottles, int numExchange) {        // 最大酒瓶数        int total = numBottles;        // 有酒瓶就兑换        while (numBottles >= numExchange) {            // 执行一轮兑换            numBottles -= numExchange;            ++total;            // 兑换一次多一个酒瓶            ++numBottles;        }        return total;    }}

代码解析

实现思路：

1. 先把所有酒喝掉 int total = numBottles；
2. 有足够的空瓶就去换一瓶酒，执行一次 while 循环；
3. 在循环中，空瓶的数量 +1，能喝到酒的数量 +1；
4. 执行下一次循环判断。

我们将以上代码提交至 LeetCode，执行结果如下：

代码实现 2：贪心改进

以上的贪心算法是一瓶酒一瓶酒进行循环兑换的，那我们可否每次将所有的空瓶子全部兑换完（可兑换的最大值），然后将兑换的酒再喝完，再进行下一次兑换？

答案是肯定的，我们只需要使用取模和取余操作就可以实现了，具体代码如下：

// 贪心 2：用 / 和 % 实现class Solution {    public int numWaterBottles(int numBottles, int numExchange) {        // 总酒瓶数        int total = numBottles;        // 有酒瓶就兑换        while (numBottles >= numExchange) {            // 最多可兑换的新酒            int n = numBottles / numExchange;            // 累计酒瓶            total += n;            // 剩余酒瓶(剩余未兑换 + 已兑换喝掉的)            numBottles = numBottles % numExchange + n;        }        return total;    }}

我们将以上代码提交至 LeetCode，执行结果如下：

总结

贪心算法初看感觉很“难”，但具体实现起来却发现很简单。其实「算法」也是一样的，初看这个词感觉很难很高大上，其实它就是解决某个问题的一种思想、一种固定的“套路”而已，也并无神秘可言。

人常说：路虽远行则将至，事虽然难做者必成。“难”和“易”从来都是相对的，其实从“难”到“易”就是一个逐渐开悟、逐渐成长的过程。

参考 & 鸣谢

https://leetcode-cn.com/problems/water-bottles/

https://www.cnblogs.com/steven_oyj/archive/2010/05/22/1741375.html

https://zh.wikipedia.org/zh-hans/贪心算法

更多精彩推荐

☞全网销售额超 2.67 亿！德施曼连续 5 年蝉联双11全网智能锁销冠
☞苹果发布首款 Mac 自研芯片 M1，贯通生态快人一步
☞详解微软 ALUM：当语言模型遇到对抗训练
☞腾讯竟然是这样招人的，哈哈哈哈哈
☞AI 隐身术，能让物体在视频中消失的魔法

☞一文教你如何在生产环境中在Kubernetes上部署Jaeger

点分享
点点赞
点在看