【论文笔记】基于骨架的动作识别的时空图卷积网络
人体骨架为人类动作识别传递了重要的信息。传统的骨架建模方法通常依赖于手工制作的部件或遍历规则,因此表达能力有限,难以推广。本文中,我们提出了一种新的动态骨架模型,称为时空图卷积网络(ST-GCN),它通过从数据中自动学习空间和时间模式,突破了以往方法的局限性。这种方法不仅具有更强的表现力,而且具有更强的泛化能力。在两个大型数据集Kinetics和NTU-RGBD上,与主流方法相比取得了实质性的改进。

动机
贡献
时空图卷积网络
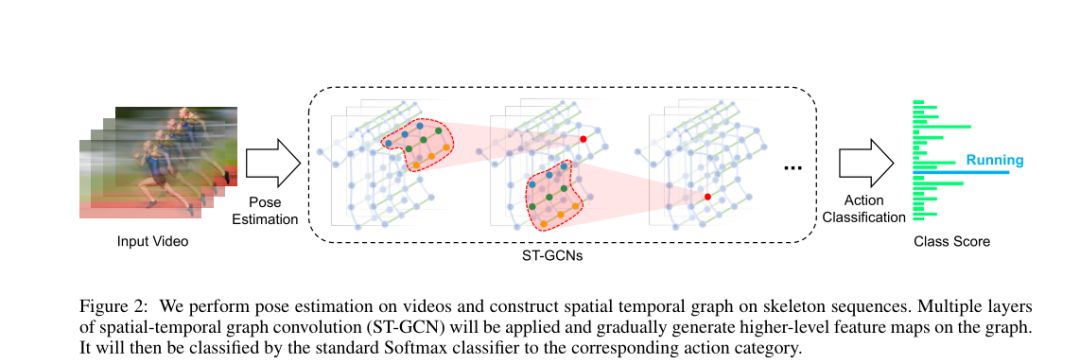
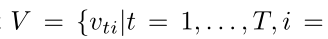
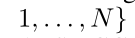
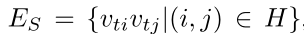
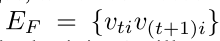
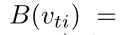
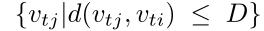
-
d(v_{tj}, v_{ti}) 表示从 v_{tj} 到 v_{ti} 的任意路径的最小长度 -
D=1,即关节节点的1-hop 邻居集
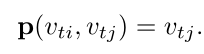
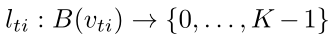
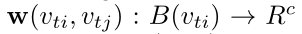
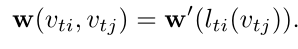
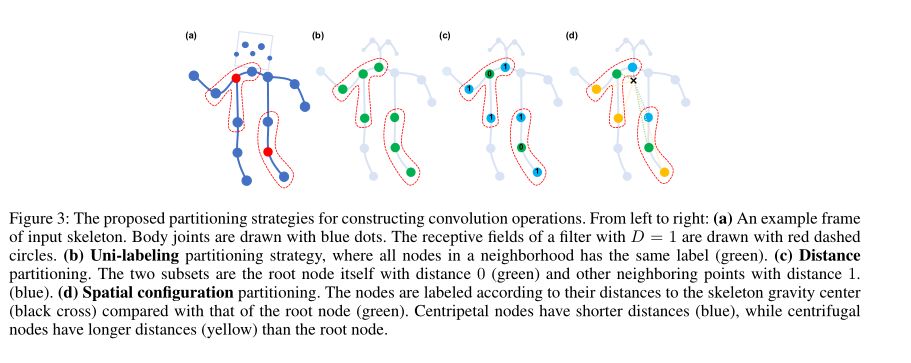
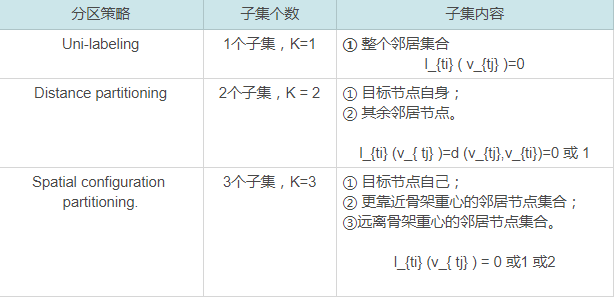
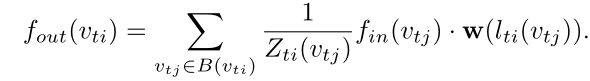
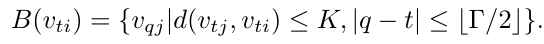
-
参数Γ控制要包括在相邻图中的时间范围,因此可以称为时间核大小。
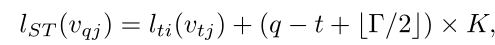
-
l_{ti}(v_{tj})是v_{tj} 处的单帧情况的标签映射。
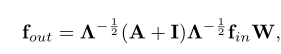
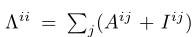
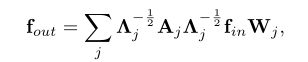
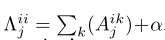
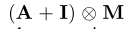
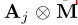
-
⊗表示两个矩阵之间的逐元素乘积。 -
掩码M初始化为全一矩阵
实验
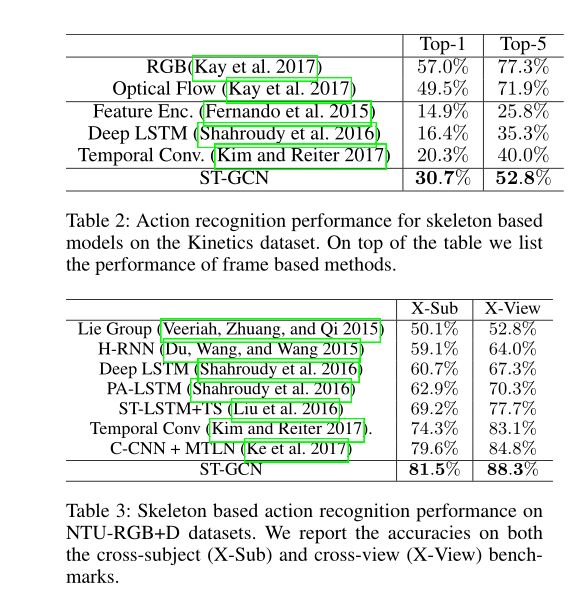
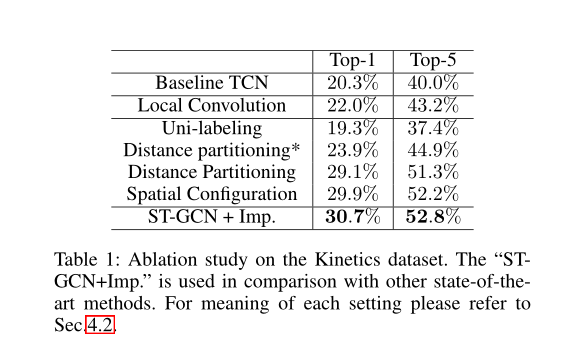
总结



登录查看更多
相关内容
专知会员服务
136+阅读 · 2020年3月8日
Arxiv
14+阅读 · 2019年3月5日
Arxiv
3+阅读 · 2017年12月28日



