贝叶斯与深度学习如何结合？看这份《贝叶斯深度学习: DL与Bayesian原理》NeurIPS2019硬核教程

2019 年 12 月 22 日 专知

【导读】NeurIPS 2019刚落下帷幕，大会发布了7篇最佳论文，一系列论文和tutorial，涉及很多热点比如图机器学习、元学习、核方法、软硬一体化等。不得不看！NeurIPS 2019三个关键研究热点趋势：贝叶斯、GNN、凸优化。来自东京RIKEN研究中心的Emtiyaz Khan给了关于以贝叶斯原理进行深度学习的教程《Deep Learning with Bayesian Principles》，共有86页ppt，以及撰写了最新的论文，讲述贝叶斯和深度学习如何结合到一起进行学习新算法，提出了一种基于贝叶斯原理的学习规则，它使我们能够连接各种各样的学习算法。利用这一规则，可以在概率图形模型、连续优化、深度学习、强化学习、在线学习和黑盒优化等领域得到广泛的学习算法。非常具有启发性，值得查看！

视频地址：

https://slideslive.com/38921489/deep-learning-with-bayesian-principles

教程地址：

https://nips.cc/Conferences/2019/Schedule?showEvent=13205

Deep Learning with Bayesian Principles

摘要

深度学习和贝叶斯学习被认为是两个完全不同的领域，通常用于互补的设置情景。显然，将这两个领域的思想结合起来是有益的，但鉴于它们的根本区别，我们如何才能做到这一点呢?

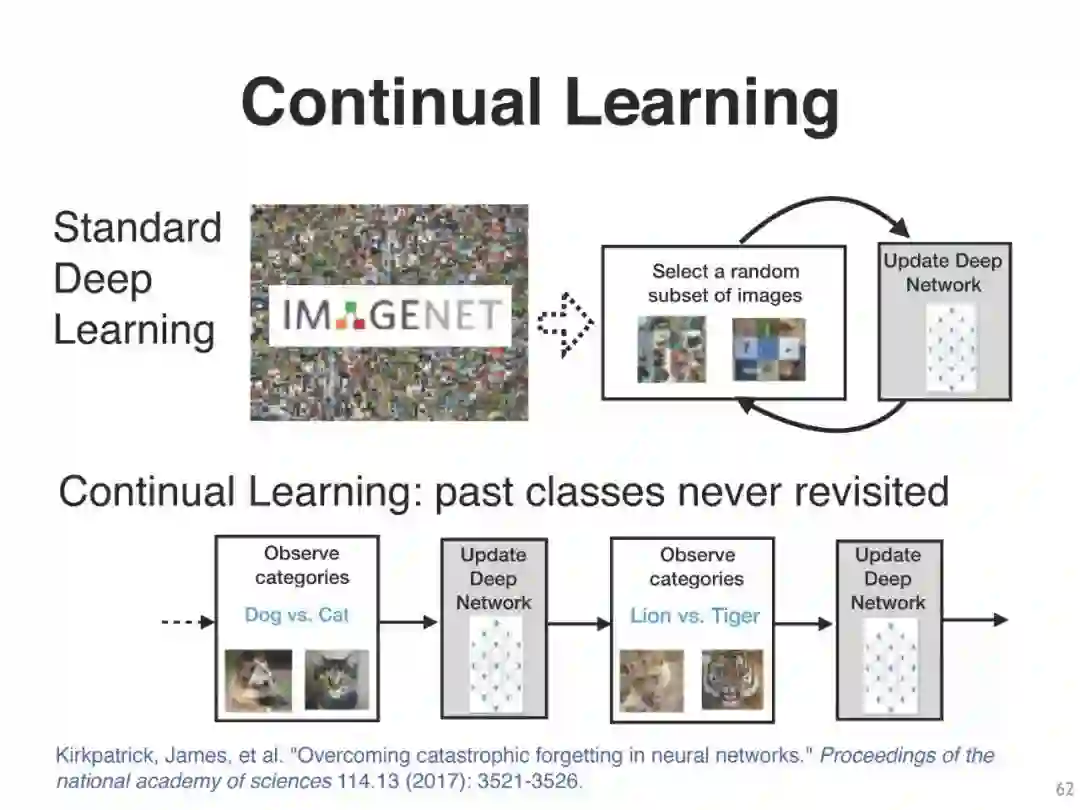
本教程将介绍现代贝叶斯原理来填补这一空白。利用这些原理，我们可以推出一系列学习算法作为特例，例如，从经典算法，如线性回归和前向后向算法，到现代深度学习算法，如SGD、RMSprop和Adam。然后，这个视图提供了新的方法来改进深度学习的各个方面，例如，不确定性、健壮性和解释。它也使设计新的方法来解决挑战性的问题，如那些出现在主动学习，持续学习，强化学习等。

总的来说，我们的目标是让贝叶斯和深度学习比以往任何时候都更接近，并激励它们一起工作，通过结合他们的优势来解决具有挑战性的现实问题。

我研究的目标

“理解从数据中学习的基本原理，并利用它们来开发可以像生物智能一样学习的算法。”

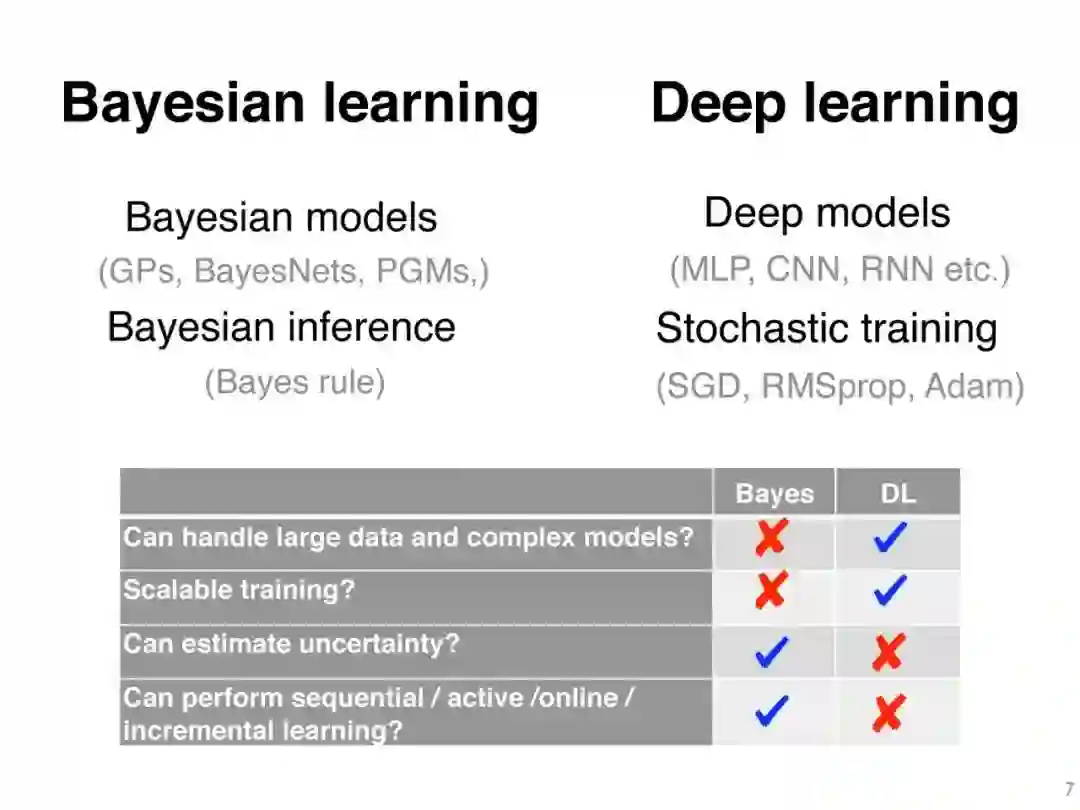
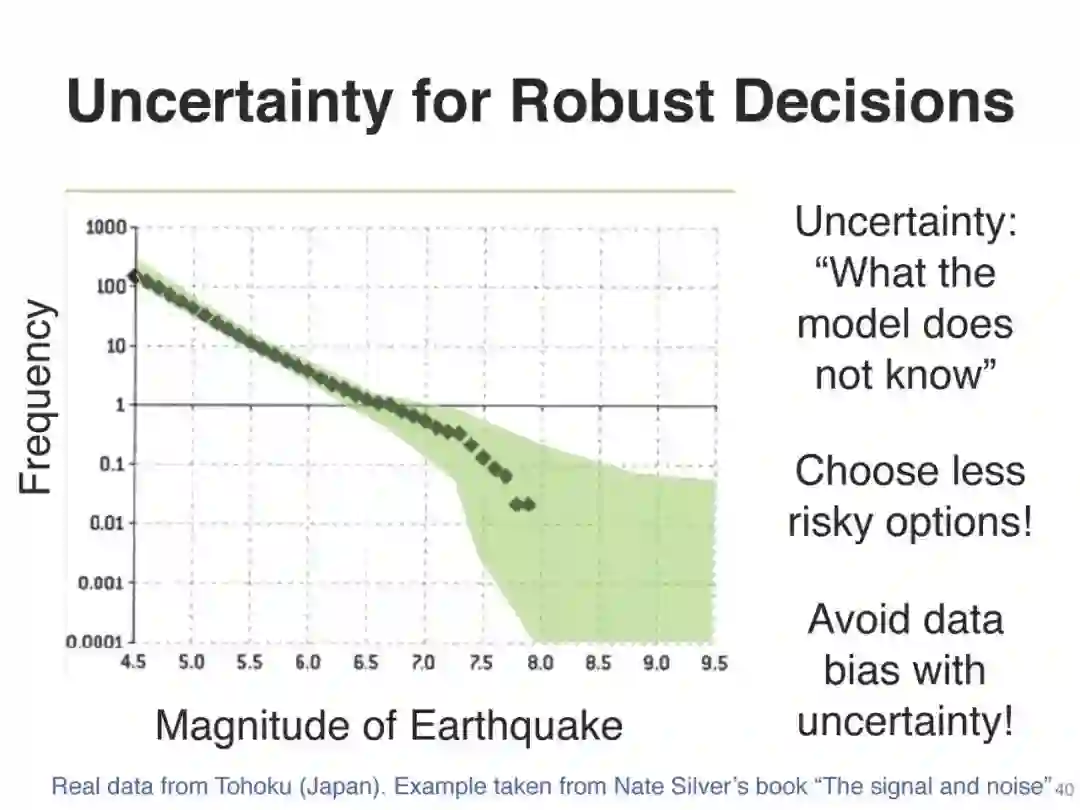
与常规的深度学习相比，贝叶斯深度学习主要有两个优点:不确定性估计和对小数据集的更好的泛化。在实际应用中，仅仅系统做出预测是不够的。知道每个预测的确定性是很重要的。例如，预测癌症有50.1%的确定性需要不同的治疗，同样的预测有99.9%的确定性。在贝叶斯学习中，不确定性估计是一个内置特性。

贝叶斯原理作为一般准则

设计/改进/推广学习算法
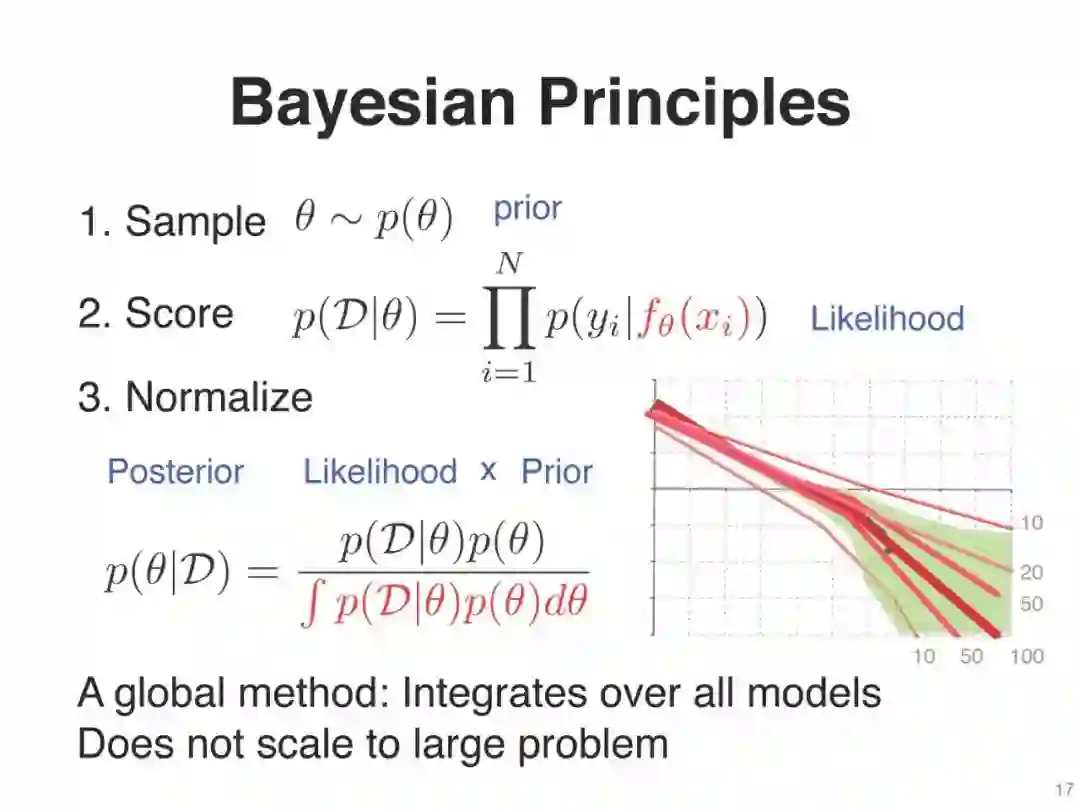
通过计算“后验近似”

衍生出许多现有的算法，

深度学习(SGD, RMSprop, Adam)
精确贝叶斯，拉普拉斯，变分推论等

设计新的深度学习算法

不确定性、数据重要性、终身学习

影响力:每件事都有一个共同的原则。

梯度下降法是利用具有固定协方差的高斯分布，并估计其均值

牛顿法是用多元高斯法推导出来的
RMSprop是使用对角协方差得到的
亚当是由添加重球动量项
对于“牛顿系综”，使用混合高斯[1]
为了推导DL算法，我们需要从“全局”近似转换到“局部”近似
然后，为了改进DL算法，我们只需要添加一些“全局”触摸到DL算法

两篇重要论文

从贝叶斯原则中学习算法

机器学习算法通常使用来自优化和统计的思想，然后通过广泛的经验努力使它们变得实用，因为缺乏指导这一过程的基本原则。在本文中，我们提出了一种基于贝叶斯原理的学习规则，它使我们能够连接各种各样的学习算法。利用这一规则，我们可以在概率图形模型、连续优化、深度学习、强化学习、在线学习和黑盒优化等领域得到广泛的学习算法。这包括经典算法，如最小二乘法、牛顿法、卡尔曼滤波，以及现代深度学习算法，如随机-梯度下降、RMSprop和Adam。总体上，我们证明贝叶斯原则不仅能统一、推广和改进现有的学习算法，而且还能帮助我们设计新的学习算法。

论文地址：

https://emtiyaz.github.io/papers/learning_from_bayes.pdf

贝叶斯原理的深度学习实践

贝叶斯方法有望解决深度学习的许多缺点，但它们很少与标准方法的性能相匹配，更不用说对其进行改进了。在本文中，我们通过自然梯度变分推断演示了深度网络的实践训练。通过应用批处理归一化、数据增强和分布式训练等技术，即使在大型数据集（例如ImageNet）上，我们也可以在与Adam优化器大致相同的训练周期内获得类似的性能。

重要的是，这种方法保留了贝叶斯原理的优势：很好地校准了预测概率，改善了分布外数据的不确定性，并提高了持续学习的能力。这项工作可以实现实用的深度学习，同时保留贝叶斯原理的优点。其PyTorch实现可作为即插即用优化器使用。