让DL可解释？这一份66页贝叶斯深度学习教程告诉你

【导读】贝叶斯深度学习对于理解深度学习这个黑盒子能提供可解释性，在深度学习理论研究中这几年也是非常地热。机器学习专家Andrew Gordon Wilson 在这个PPT教程详细讲述了模型选择、贝叶斯和频率的区别、贝叶斯推断、预测分布、Beta分布、高斯过程、神经网络、以及作者最新提出的Bayesian GAN。

为什么需要使用贝叶斯深度学习（Bayesian Deep Learning）?

• 一个强大的模型构建和理解泛化框架，

  
  

• 不确定性表示(决策的关键)，

  
  

• 更好的点估计

  
  

• 这是第二波神经网络结束时最成功的方法（Neal，1998），

  
  

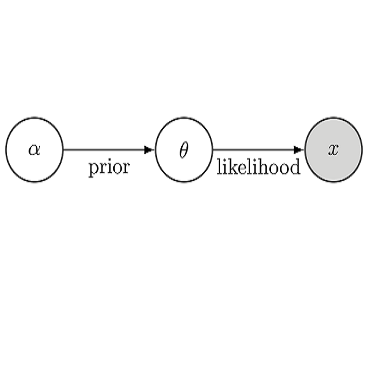
• 从概率论的角度来看，神经网络并不那么神秘。

为什么不呢?

• 可能在计算上难以处理（但不必如此，作者提出很多解决方法）

  
  

• 可能涉及很多个模块（但不一定）

在过去的两年里，作者将这些局限性作为一个非常富有成果的研究方向的一部分，并取得了令人振奋的进展。详细见PPT内容。

摘要

生成对抗网络（GANs）可以隐式地学习图像，音频和数据上丰富的分布表示，这些分布难以显式地进行建模。 作者提出了一种实用的贝叶斯公式，用于使用GAN进行无监督和半监督学习。 

在此框架内，作者使用随机梯度哈密顿蒙特卡罗（Hamiltonian Monte Carlo）来边缘化生成器和判别器网络的权重。 这种方法简单直观，并且在没有任何标准干预（比如标签平滑或小批量判别）的情况下获得良好的性能。 通过探索生成器参数的表达后验，Bayesian GAN避免了模型崩溃，产生了可解释和多样化的候选样本，并为包括SVHN，CelebA和CIFAR-10在内的基准测试提供半监督学习的最好的（state-of-the-art）定量结果。 并且表现优于DCGAN，Wasserstein GAN和DCGAN。

https://arxiv.org/abs/1705.09558

https://github.com/andrewgordonwilson/bayesgan

请关注专知公众号（扫一扫最下面专知二维码，或者点击上方蓝色专知），

• 后台回复“BDL2018” 就可以66页的 贝叶斯深度学习PPT 下载链接~ 

作者主页链接：

https://people.orie.cornell.edu/andrew/

附PPT原文：

-END-

专 · 知

人工智能领域主题知识资料查看与加入专知人工智能服务群：

【专知AI服务计划】专知AI知识技术服务会员群加入与人工智能领域26个主题知识资料全集获取。欢迎微信扫一扫加入专知人工智能知识星球群，获取专业知识教程视频资料和与专家交流咨询！

请PC登录www.zhuanzhi.ai或者点击阅读原文，注册登录专知，获取更多AI知识资料！

请加专知小助手微信（扫一扫如下二维码添加），加入专知主题群（请备注主题类型：AI、NLP、CV、 KG等）交流~

请关注专知公众号，获取人工智能的专业知识！

点击“阅读原文”，使用专知