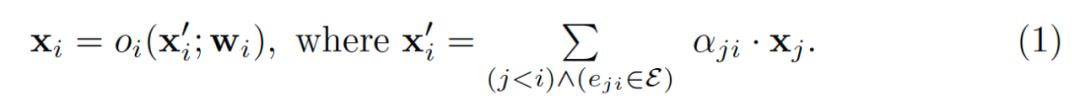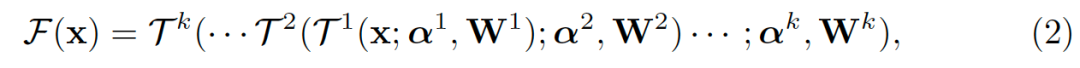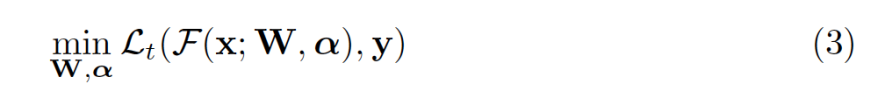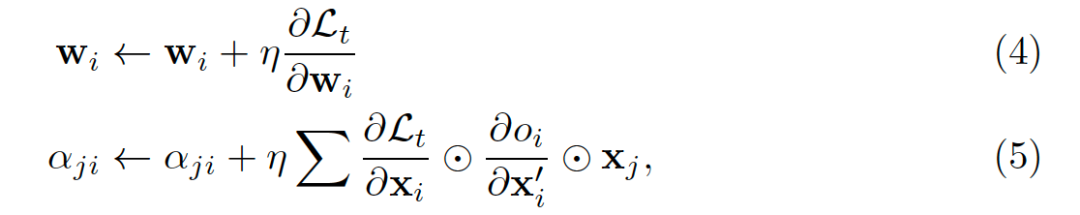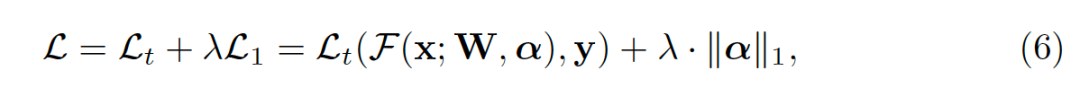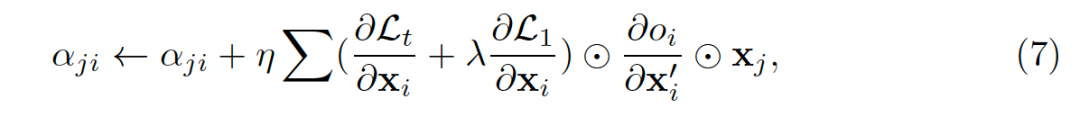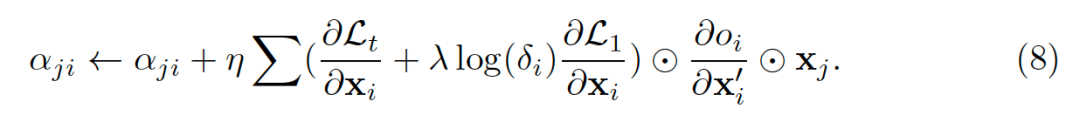![]()
本文是计算机视觉领域顶级会议 ECCV 2020 入选论文《Learning Connectivity of Neural Networks from a Topological Perspective》的解读。
作者 | 袁 坤
编辑 | 青 暮
在ECCV 2020上,商汤研究院深度学习中间件组提出的拓扑视角为分析神经网络的优化过程提供了一种新的思路。
在设计神经网络的深度、卷积类型、归一化层和非线性层之外,我们提出对神经网络的拓扑连接进行优化,来取代以往的堆叠或手工设计的连接方式。通过将网络表示为有向无环图,并向边赋予可学习的权重来表示连接的重要程度。整个优化过程可以通过可微分的方式进行。进一步地,我们对连接的分布添加额外的稀疏约束,使得重要的连接得以保留,移除不重要的连接,进一步提升网络的性能和泛化能力。这种优化方式可以很好的和现有的网络结构进行结合。实验结果表明优化得到的连通方式超过了传统的基于规则设计连接,包括随机的、残差的和完全图的。在不额外增加过多参数量和计算量的基础上,在ImageNet图像分类和COCO目标检测上取得了明显的提升。
简介和动机
深度学习成功地将特征工程从手工设计转移到自动学习。这标志着从样本到特征的映射可以根据不同的任务来进行优化学习。作为一种趋势,寻找有效的神经网络结构是一个重要且具有实际价值的方向。但是结构的设计依旧充满挑战且耗时。部分研究工作关注于网络的深度、卷积的类型、归一化和非线性操作等。在这些维度之外,也有一些工作尝试在网络的拓扑连接上进行改进。从VGGNet、GoogleNet、Highway到ResNet、MobileNet-v2、ShuffleNet,网络的拓扑连接从平原拓扑发展到残差拓扑,一定程度上缓解了网络加深带来的梯度消失和爆炸问题。不同于这些相对稀疏的连接形式,DenseNet提出将层与层之间全部连接复用特征表示。现有的一些网络结构搜索(NAS)方法也尝试进行连接方式的搜索。在一定程度上,这些拓扑层面的改进反映了拓扑连接对优化过程的影响。但是为了平衡设计成本和性能,这些网络大多采用堆叠的方式来构建最终的结构,一定程度上限制了拓扑的可能性。因此,我们思考:神经网络的连通性可以被优化吗?合适的方法是什么?
神经网络的拓扑视角
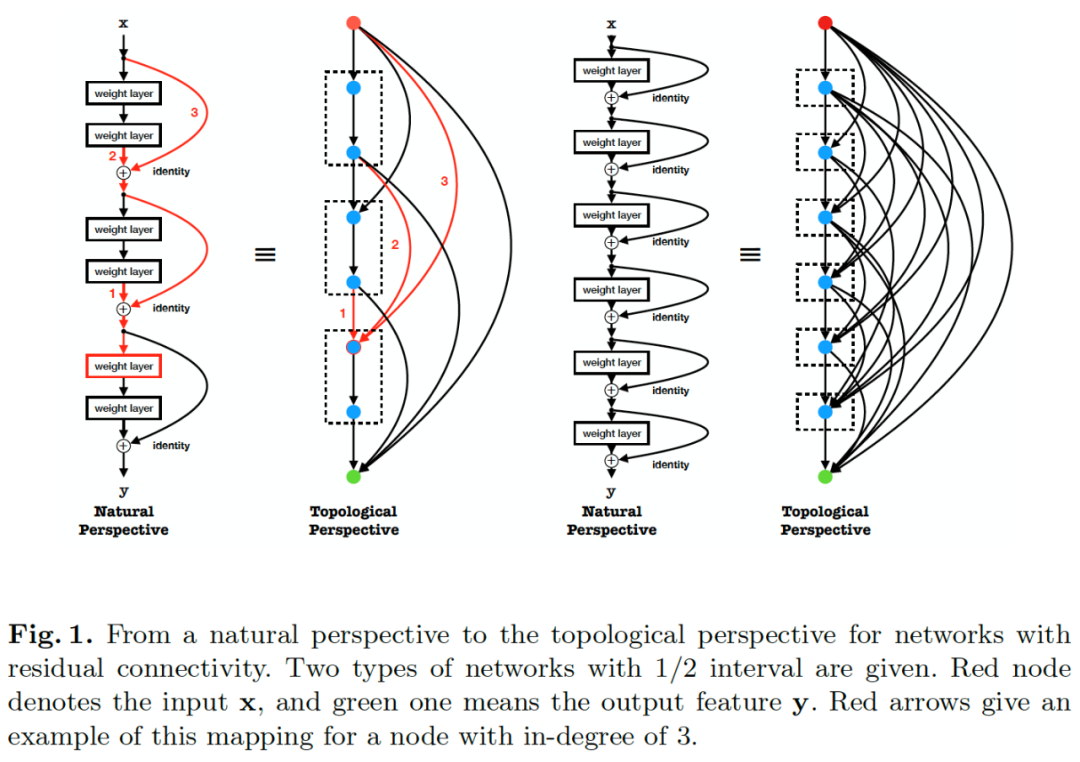
为了回答这些,我们提出一种新的拓扑视角来表达分析现有的网络结构。如图1所示,网络被表示为有向无环图(DAG),其中特征融合、卷积计算、归一化和非线性等特征计算被表示为节点,层与层之间的连接被表示为边,反映信息流的传递。图1给出了残差拓扑连接所对应的拓扑形式,我们首次展示了残差的拓扑连接是一种相对稠密的连接形式,当残差的间隔为1时,网络可以被表示为完全图(complete graph),即各个节点之间均有边连接。所有节点可以直接从输入获取特征,从输出获得梯度更新,这在一定程度上解释了残差连接能够有效的原因。
![]()
数学形式上,我们将拓扑视角下的网络结构表示为图
![]() ,其中
表示节点的集合,
表示边的集合。在图中的每一个节点
进行特征变换操作
,参数表示为
,其中
表示节点的拓扑顺序。同时
,其中
表示节点的集合,
表示边的集合。在图中的每一个节点
进行特征变换操作
,参数表示为
,其中
表示节点的拓扑顺序。同时
![]() 表示从节点
到节点
的边,其中
反映了连接的重要程度。在前向计算的过程中,每个节点从存在连接的前序节点获得特征输入,然后经过变换得到特征
。之后被输送到存在连接的后续节点中,节点的操作可以被表示为:
表示从节点
到节点
的边,其中
反映了连接的重要程度。在前向计算的过程中,每个节点从存在连接的前序节点获得特征输入,然后经过变换得到特征
。之后被输送到存在连接的后续节点中,节点的操作可以被表示为:
![]()
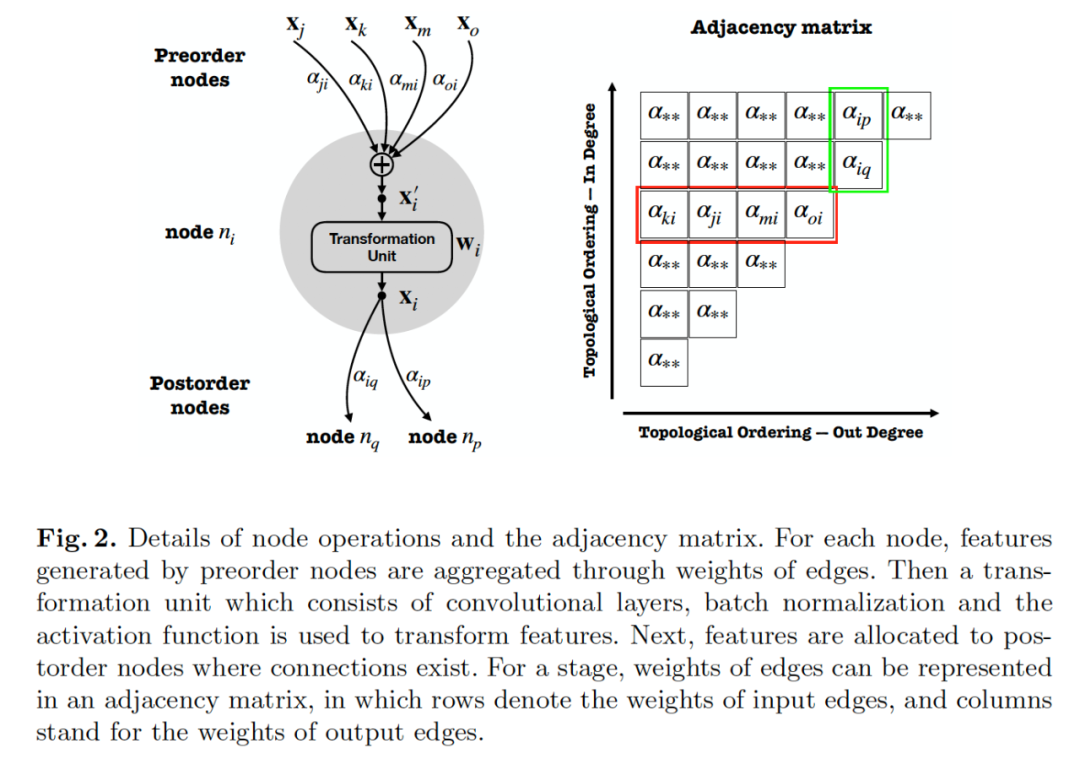
在一个图中,第一个节点被指定为输入节点,只进行特征的分发不进行计算;最后一个节点被指定为输出节点,只从前序节点获取输入并进行融合作为图的输出特征。我们提出使用邻接矩阵来存储边的权重,如图2右侧所示,矩阵的行表示输入边的权重,列表示输出边的权重。
![]()
对于一个由
个阶段组成的网络结构,
个DAG被初始化为首尾相连,每个图通过输入或者输出节点与前序或者后续的图相连。对于输入
和对应的标签
,从样本到特征的表示可以被写作:
![]()
优化空间的定义
在定义了拓扑视角之后,现有的大部分网络可以被表示。其中由图1演变来的完全图可以被用来作为优化空间。不同于以往的连接是通过堆叠模块进行构建,完全图提供了所有可能的连接。对于一个具有个节点的图,其中包含的离散子图有
![]() 种可能,对于一个有个图组成的网络,总的搜索空间包含
种可能,对于一个有个图组成的网络,总的搜索空间包含
![]() 种可能,比现有的基于模块的方法拥有更大的搜索空间。在对边添加了相应的权重之后,图变换为带权重的图(weighted graph),寻找最优的拓扑连通结构转换为在完全图下寻找最优的子图,并且可以通过优化连续的权重获得。
种可能,比现有的基于模块的方法拥有更大的搜索空间。在对边添加了相应的权重之后,图变换为带权重的图(weighted graph),寻找最优的拓扑连通结构转换为在完全图下寻找最优的子图,并且可以通过优化连续的权重获得。
拓扑连通性的优化方法
我们提出一种可微分的方式来优化网络的连通性。通过学习连续的边上权重组成的集合,优化过程可以和现有的梯度下降更新方式兼容,对应任务的损失函数可以定义为
。不同于MaskConnect [1],我们没有将连接的权重进行二值化,这允许不同的特征拥有区分性的权重。不同于DARTS [2]选取概率最大的操作(operation),我们进行连续的特征融合方式,这能够保持训练和测试的一致性。优化目标可以表示为:
![]()
如果将
对应的反传梯度表示为
,对应的的梯度表示为
,那么网络参数和拓扑连接对应的更新方式可以被表示为:
![]()
由于不同层产生的特征具有不同的语义信息,他们会对后续的节点贡献不同的权重。类似于生物中的神经连接机制,突触在幼儿的早期阶段会被创建,随着生长的过程重要程度被重新建立,成长为相对稀疏的连接。相同的稀疏特性也在哈希检索上验证了有效性。为了利用稀疏特性带来的优势,我们对拓扑的分布添加额外的L1稀疏约束,来惩罚非零的权重向零靠拢。这个稀疏约束让连接更关注重要的部分,移除不重要的连接,以此来增加网络的泛化能力。优化目标可以被重新定义为:
![]()
针对不同图的性质,我们提出两种稀疏优化方式,均匀稀疏和自适应稀疏。均匀稀疏对不同的边赋予相同的约束,边上权重的更新方式可以被表示为:
![]()
自适应稀疏会根据节点的输入边的数量决定,对于节点拥有较多输入边,这些边会受到较大的约束。这种约束保证了信息流的平滑同时避免拥有较少边的节点被关闭,这种更新方式可以表示为:
![]()
![]()
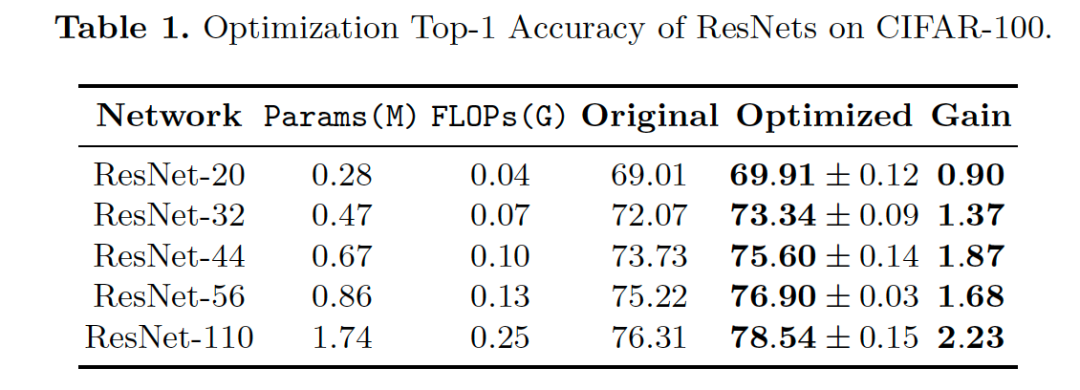
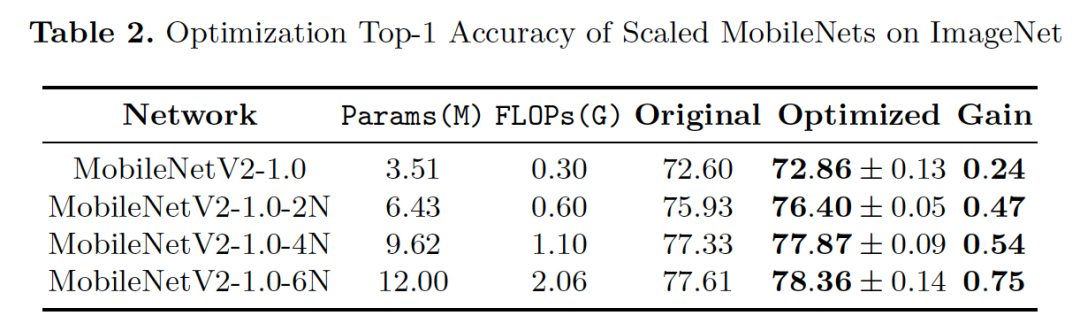
对现有神经网络的优化实验
我们的优化方式可以和现有的网络结构很好地适应,通过将网络表示为拓扑视角下的DAG形式,我们对ResNet和MobileNet进行优化,优化结果在CIFAR100和ImageNet上取得了较好的提升。特别地,在Mobile Setting下,我们优化得到的结构在ImageNet上可以取得76.4%的Top-1准确度。
![]()
![]()
更大优化空间下的对比实验
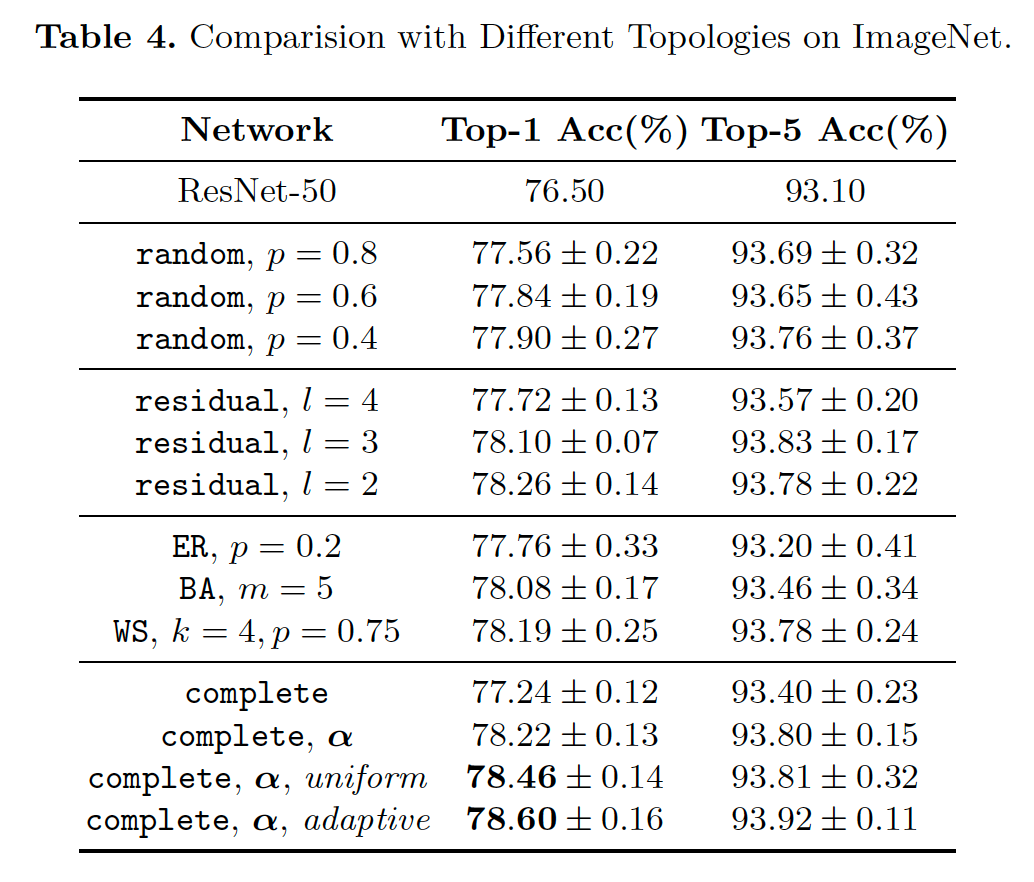
受限于现有网络较小的优化空间,拓扑结构只能在较小的范围内优化,限制了拓扑的表示能力。因此本节我们提出了一个更大的优化空间,并在这个优化空间下更严格的比较不同拓扑连接的性能差异。该优化空间的定义如表3所示。我们在相同的计算量下比较了随机、残差和完全图。随机图可以通过RandWire[3]中使用的ER、BA、WS生成器生成。实验结果如表4所示。
![]()
实验结果表明:(1)拓扑连通性对网络的优化和最终的性能影响很大;(2)通过设置随机网络的不同
值和残差网络的不同
值,说明性能和网络的稀疏程度相关;(3)对于完全图,引入额外的边上的权重可以带来Top-1上0.98%的提升;(4)通过添加稀疏约束,网络的性能可以获得进一步的提升,对于添加自适应稀疏约束的完全图可以获得78.6%的Top-1精度;(5)这些反映了神经网络的拓扑连接可以被优化,而且优化得到的结构不亚于手工设计的规则,包括随机、残差等。
![]()
![]()
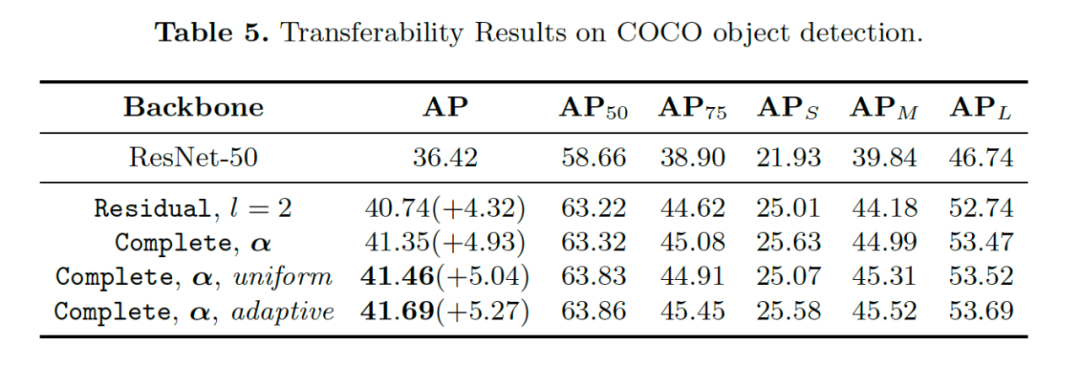
在目标检测上的实验也验证了这种方法具有良好的迁移和泛化能力,结果如表5所示。
优化过程的可视化分析
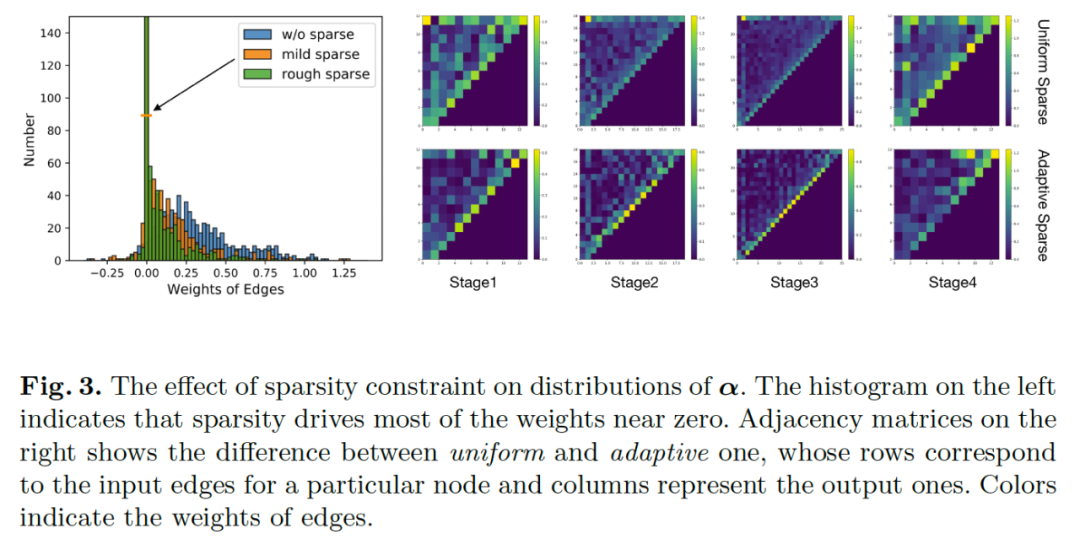
我们分析了稀疏约束对拓扑连接对应的权重的分布影响,并进行了可视化分析。大部分的连接权重被置为零,留下了相对重要的连接。
![]()
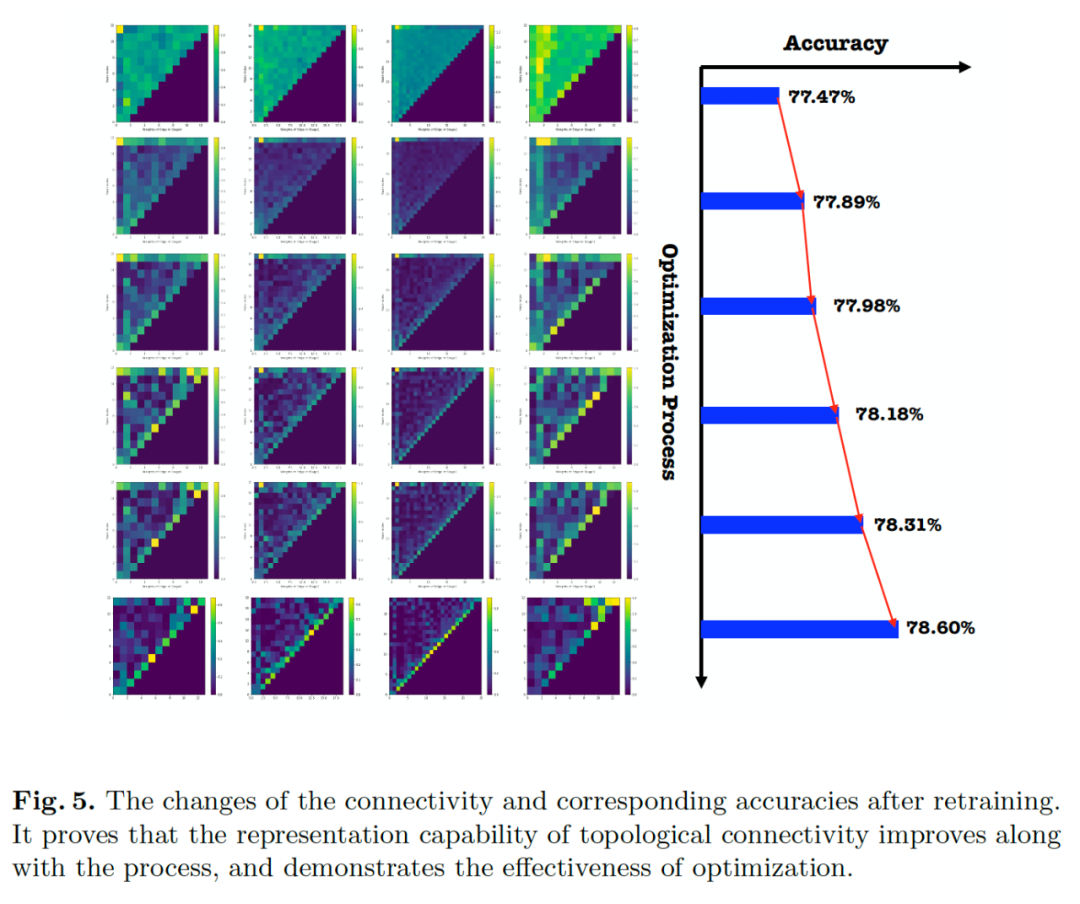
由于网络的参数和拓扑是被联合优化的,为了验证拓扑连接本身的优化有效性,我们在优化过程中采样结构并将拓扑参数固定从头开始训练网络本身的参数。可以看出在训练的初始阶段连接相对稠密,随着训练过程不同要的连接逐渐消失,保留下相对重要的连接,网络的表示能力也是逐渐提升的。
![]()
总结与展望
在这篇工作中我们提出一种可微分的方式优化神经网络的拓扑连接。通过定义的拓扑视角并添加额外的权重将寻找最优的拓扑连接转化为在完全图中寻找最优的子图。优化方式可以和梯度下降很好地适应。通过对拓扑连接的分布添加额外的稀疏约束,重要的连接被保留,提升了拓扑结构的性能和泛化能力。在图像分类和目标检测上的实验也验证了方法的有效性,证明神经网络的拓扑结构可以被优化,优化得到的结构优于手工或先验设计的结构。未来可以尝试对NAS生成的结构进一步优化。
[1]Ahmed, K., Torresani, L. Maskconnect: Connectivitylearning by gradient descent. ECCV 2018.
[2]Liu, H., Simonyan, K., Yang, Y. Darts: Differentiablearchitecture search. ICLR. 2018
[3] Xie, S., Kirillov, A., Girshick, R., He, K.Exploring randomly wired neural networks for image recognition. ICCV 2019
阅读原文,直达“ ECCV”小组,了解更多会议信息!
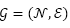 ,其中
表示节点的集合,
表示边的集合。在图中的每一个节点
进行特征变换操作
,参数表示为
,其中
表示节点的拓扑顺序。同时
,其中
表示节点的集合,
表示边的集合。在图中的每一个节点
进行特征变换操作
,参数表示为
,其中
表示节点的拓扑顺序。同时
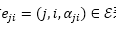 表示从节点
到节点
的边,其中
反映了连接的重要程度。在前向计算的过程中,每个节点从存在连接的前序节点获得特征输入,然后经过变换得到特征
。之后被输送到存在连接的后续节点中,节点的操作可以被表示为:
表示从节点
到节点
的边,其中
反映了连接的重要程度。在前向计算的过程中,每个节点从存在连接的前序节点获得特征输入,然后经过变换得到特征
。之后被输送到存在连接的后续节点中,节点的操作可以被表示为:
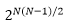 种可能,对于一个有个图组成的网络,总的搜索空间包含
种可能,对于一个有个图组成的网络,总的搜索空间包含
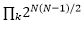 种可能,比现有的基于模块的方法拥有更大的搜索空间。在对边添加了相应的权重之后,图变换为带权重的图(weighted graph),寻找最优的拓扑连通结构转换为在完全图下寻找最优的子图,并且可以通过优化连续的权重获得。
种可能,比现有的基于模块的方法拥有更大的搜索空间。在对边添加了相应的权重之后,图变换为带权重的图(weighted graph),寻找最优的拓扑连通结构转换为在完全图下寻找最优的子图,并且可以通过优化连续的权重获得。