加入极市专业CV交流群,与 10000+来自港科大、北大、清华、中科院、CMU、腾讯、百度 等名校名企视觉开发者互动交流!
同时提供每月大咖直播分享、真实项目需求对接、干货资讯汇总,行业技术交流。关注 极市平台 公众号 ,回复 加群,立刻申请入群~
1 Introduction
2 卷积
-
一维连续卷积
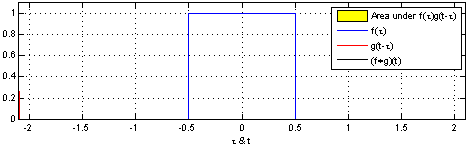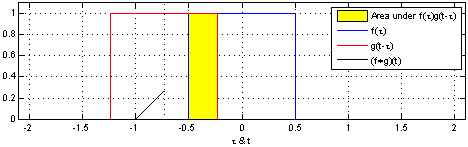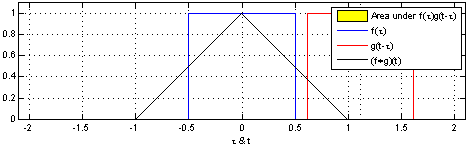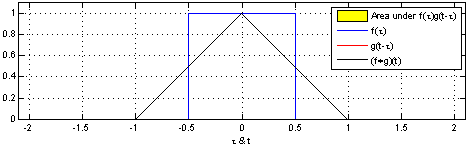
-
二维连续卷积(这里不太重要,理解是怎么算的就行)
-
一维离散卷积
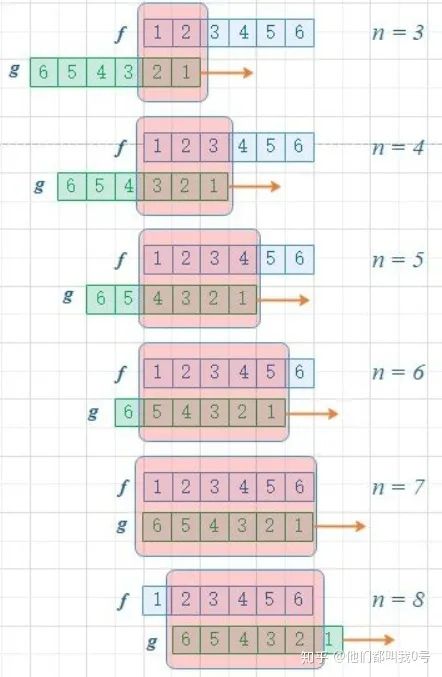
-
二维离散卷积

3 傅里叶变换与卷积的另一种求法
4 拉普拉斯算子
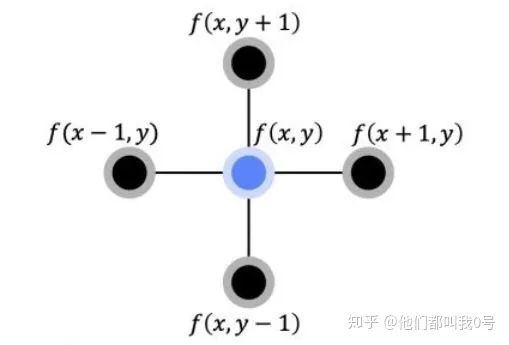
5 拉普拉斯矩阵
-
性质1:拉普拉斯矩阵有
-
性质2:特征值非负
-
性质3:特征向量相互正交
6 图傅里叶变换与图卷积
7 基于谱方法的各种Net
7.1 Spectral Graph CNN
-
在此之前我们讨论的 -
-
-
模型不是spatial localization(局部连接)的; -
依赖矩阵分解,前传的时候多次用到矩阵乘法,计算代价大; -
卷积核的规模参数
7.2 ChebNet
-
-
-
假设小于
-
7.3 平时看到的GCN——ChebNet的一阶近似
8 GCN——一个低通滤波器
8.1 为什么叫它低通滤波器?
8.2 GCN的大问题——Over Smoothing
一些很优秀的参考资料(可下滑)
[1]图表示学习极简教程: https://zhuanlan.zhihu.com/p/112295277
[2]图表示学习极简教程: https://zhuanlan.zhihu.com/p/112295277
[3]ICT沈老师相关知识: https://link.zhihu.com/?target=https%3A//www.bilibili.com/video/BV1zp4y117bB
[4]拉普拉斯矩阵的范例: https://link.zhihu.com/?target=https%3A//en.wikipedia.org/wiki/Laplacian_matrix
[5]图表示学习极简教程: https://zhuanlan.zhihu.com/p/112295277
[6]从 Graph Convolution Networks (GCN) 谈起: https://zhuanlan.zhihu.com/p/60014316
[7]图神经网络在线研讨会2020丨图表示学习和图神经网络的最新理论进展和应用探索: https://link.zhihu.com/?target=https%3A//www.bilibili.com/video/BV1zp4y117bB
[8]Graph Convolutional Network图卷积网络基础理论: https://zhuanlan.zhihu.com/p/100250297
[9]深入浅出图神经网络: https://link.zhihu.com/?target=https%3A//detail.tmall.com/item.htm%3Fspm%3Da230r.1.14.1.21e24bf49k0WwP%26id%3D610178053512%26cm_id%3D140105335569ed55e27b%26abbucket%3D9
[10]图卷积网络 GCN Graph Convolutional Network(谱域GCN)的理解和详细推导: https://link.zhihu.com/?target=https%3A//blog.csdn.net/yyl424525/article/details/100058264
[11]拉普拉斯矩阵: https://link.zhihu.com/?target=https%3A//en.wikipedia.org/wiki/Laplacian_matrix%23Incidence_matrix
[12]从 Graph Convolution Networks (GCN) 谈起: https://zhuanlan.zhihu.com/p/60014316
[13]Convolutional Neural Networks on Graphswith Fast Localized Spectral Filtering: https://link.zhihu.com/?target=https%3A//arxiv.org/abs/1606.09375
[14]Wavelets on Graphs via Spectral Graph Theory: https://link.zhihu.com/?target=https%3A//arxiv.org/abs/0912.3848
[15]Spectral Networks and Deep Locally ConnectedNetworks on Graphs: https://link.zhihu.com/?target=https%3A//arxiv.org/abs/1312.6203
[16]SEMI-SUPERVISED CLASSIFICATION WITH GRAPH CONVOLUTIONAL NETWORKS: https://link.zhihu.com/?target=https%3A//arxiv.org/pdf/1609.02907.pdf
[17]Graph Convolutional Networks: https://link.zhihu.com/?target=https%3A//tkipf.github.io/graph-convolutional-networks/