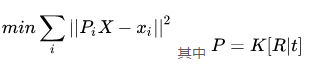干货 | CCCV 2017讲习班笔记-基于图像的大规模场景三维重建（上）

AI科技评论按，本文作者究竟灰，本文首发于知乎，AI科技评论获其授权转载。

今天去CCCV2017讲习班听了中科院自动化所模式识别国重实验室的申抒含老师和崔海楠老师的关于基于凸显的大规模场景三维重建的讲习班，把笔记整理了一下。（本文为上篇，内容为第一章：简介和第二章：稀疏重建。）

主要分为四点展开：

1. 简介

2. 稀疏重建sfm

3. 稠密重建mvs

4. 资源

1、简介

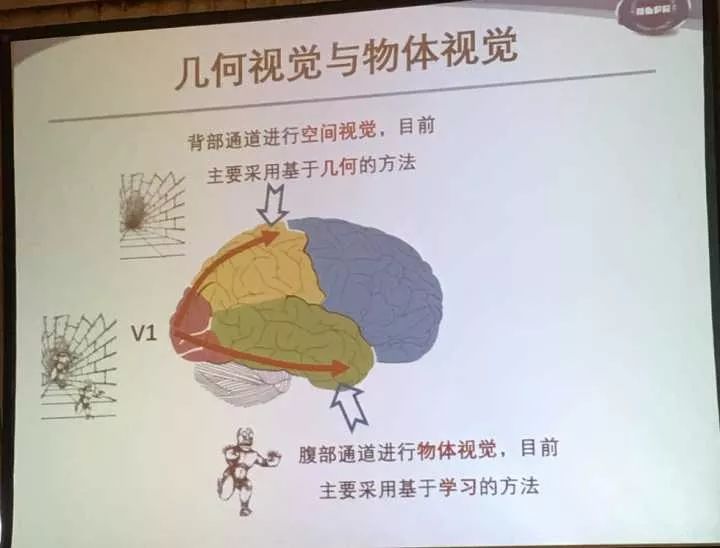
首先讲了现在cv与类脑。

1. 脑的腹部通道进行物体视觉，现在CV上主要采用基于学习的方法。

2. 脑的背部通道进行空间视觉，现在CV上主要采用基于几何的方法。

3. 最后上述两者信息在前额汇集，综合处理。

接着讲了几何视觉的核心问题：主要是机器人在三维环境中需要：

1. 对二维图像理解

2. 对三维环境感知

而三维结构和相机的六自由度空间位姿是机器人感知决策动作的基础信息。

接着讲了图像三维重建的基本流程：

基本流程包括：

1. 多视角图像

2. 图像特征提取匹配

3. 稀疏重建Sfm

4. 稠密重建MVS

5. 点云模型化

6. 生成三维模型

然后科普了一下一些基础知识：

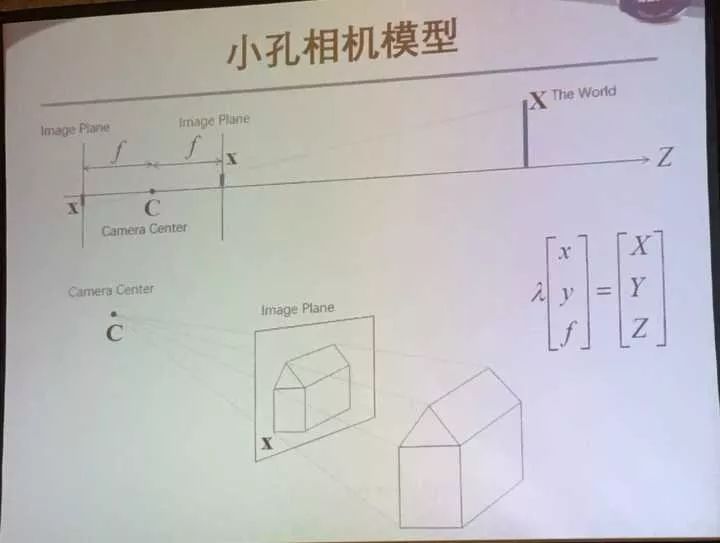
小孔成像：世界中的一个点经过小孔在图像平面上会形成一个倒立缩小的像。这就形成了几何相似三角形关系。如果我们把成像平面放到前面来，就是正立缩小的像。具体的焦距、图像片面，相机中心什么就不赘述了。右下角公式表示通过一个 相似性（比例λ）

然后说到了无穷远元素。它们用现在的xyz方法没办法表示。

于是提出了射影空间，齐次坐标是射影空间的坐标表达方式：一般的坐标在xyz后面加一个1，无穷远点最后一个为0.

当然齐次非齐次的坐标转换通过除以最后一个 w来实现。

这里有一个等价关系，即当非齐次坐标通过除以一个值 λ之后变成齐次而与一个已经存在的齐次坐标相等时为：齐次坐标在相差一个尺度时的等价。

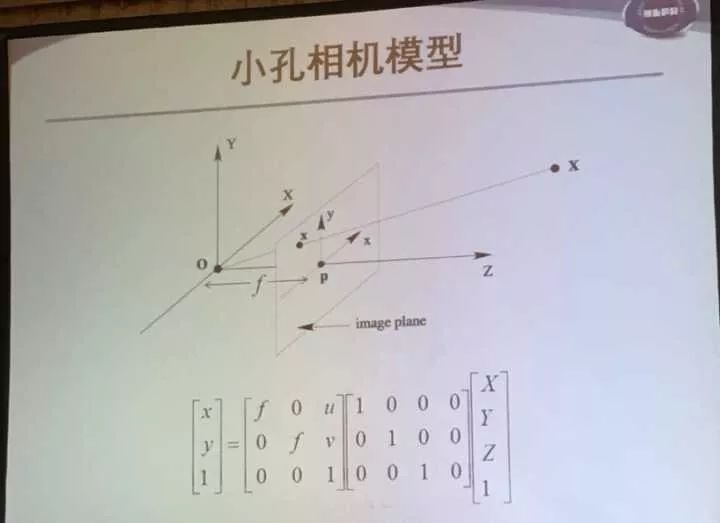
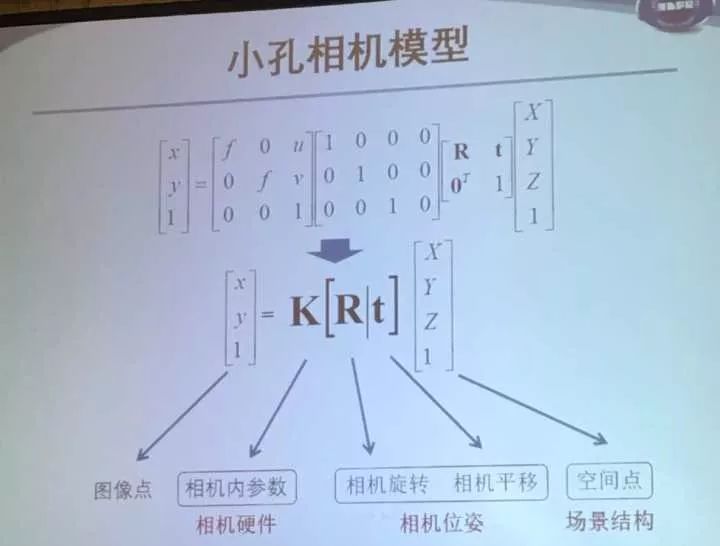
那么小孔成像模型可以表达出来。∫为焦距，u，v为主点：光心与相机平面的交点。

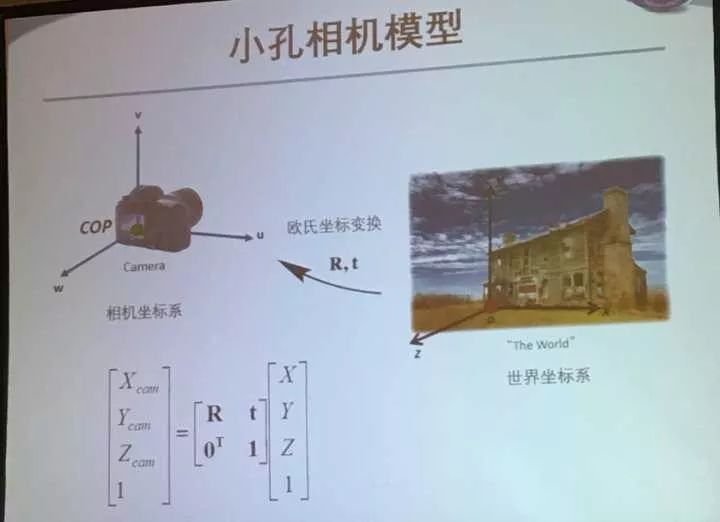
接着介绍了相机坐标系和世界坐标系之间存在一个欧式坐标变换：

中间的矩阵由R转移矩阵和t平移向量组成。

把两个式子写到一起：

可以得到图像点和空间点的关系。通过相机内参数K 、相机旋转R和相机平移建立关系。

相机的内参数由相机硬件决定，而旋转平移由相机位姿决定。空间点是场景结构点。

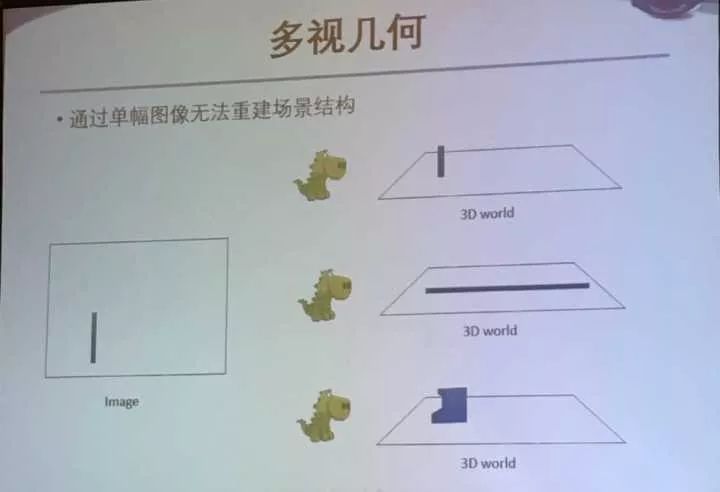
接着说了由单张图是无法重建场景结构的。

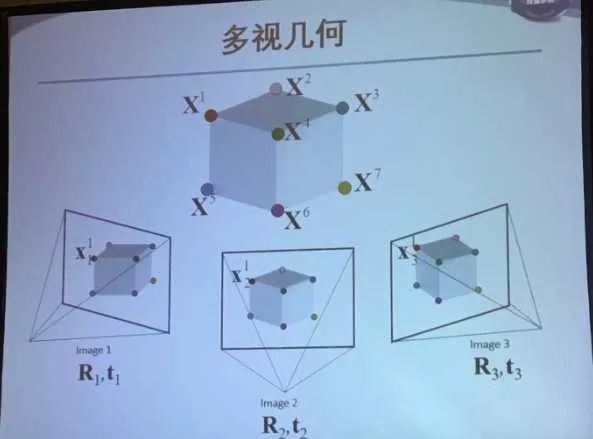
于是引出了多视图几何

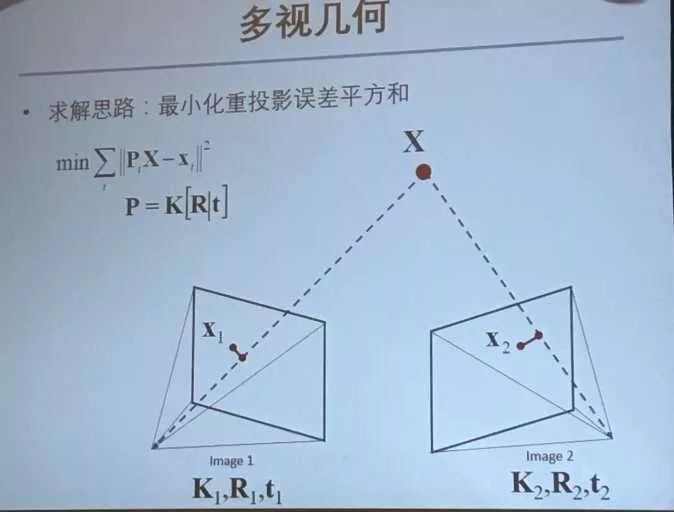
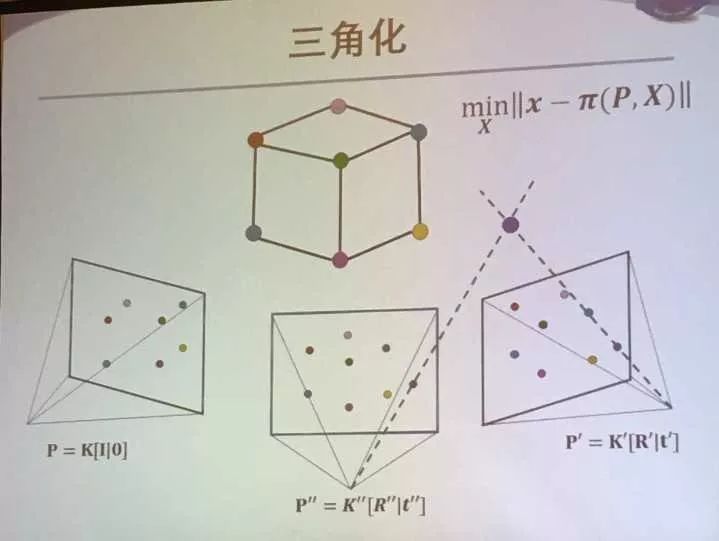
然后说求解思路：最小化重投影误差平方和

即空间点X通过之前说的坐标变换（左乘P投影到图像平面上）与图像平面上的x可以产生一个L2范数作为误差。建立一个目标函数为所有点的误差和。

接着推导就可以写成 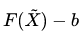的形式。

这样求解重投影误差最小化问题是一个高维非线性最小二乘问题。未知数数量由图像数量乘以旋转矩阵、平移向量、内参数、畸变加上稀疏点数目乘以世界坐标X。

求解可以用捆绑调整的工具做。Bundle Adjustment.它是一种启发式的阻尼高斯牛顿法。

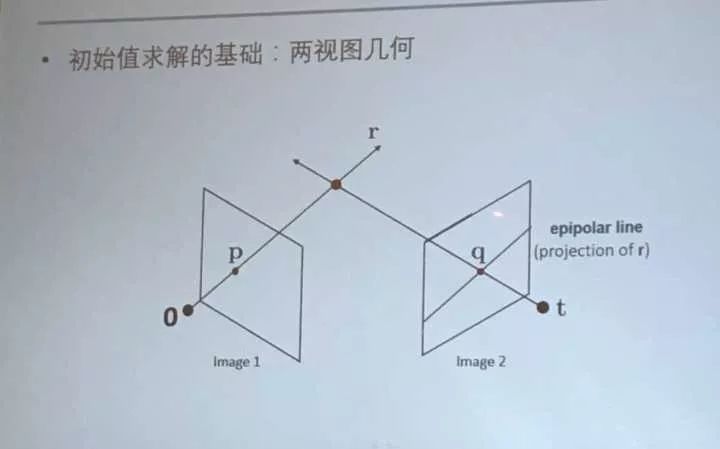
因为要做初始值求解，接着科普两视图几何：

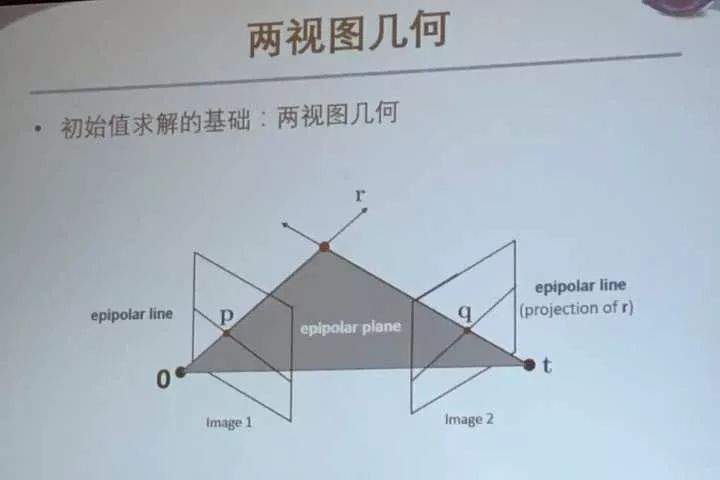
平面1上面的点p与其相机中心o连线，延长。这个线r在平面2中投影出一条极线。

同理也可以在平面1投影出极线。连接 o t这条线叫基线。这三条线在一个平面上，这个平面叫做极平面。

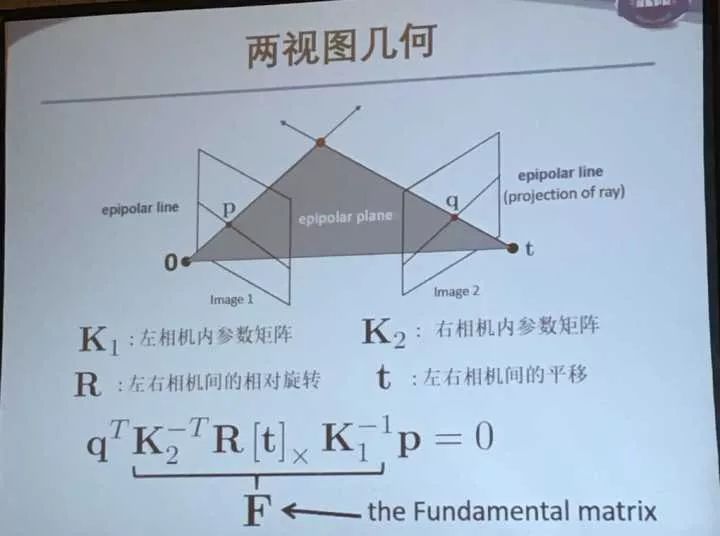
于是可以推出一个基本矩阵Fundamental matrix。

当内参K1，K2已知，用 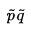表示之后，可以推出本质矩阵Essential matrix。

双视图几何的求解方法：

1. 基本矩阵可以用8点法求解，本质矩阵可以用5点发求解。

2. 通过SVD分解可以从本质矩阵中分解相机的R t.

3. 已知K R T可以三角花求解三维点X

4. 这样可以得到两视图重建的初始值，接着可以用BA进行非线性优化。

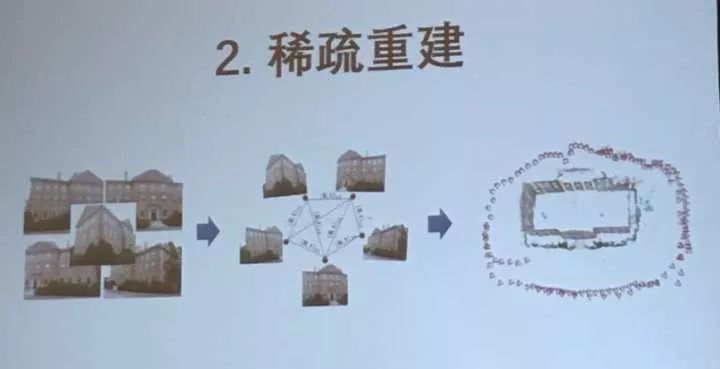
2、稀疏重建

稀疏重建是通过相机运动恢复场景结构。（Structure-from-Motion）

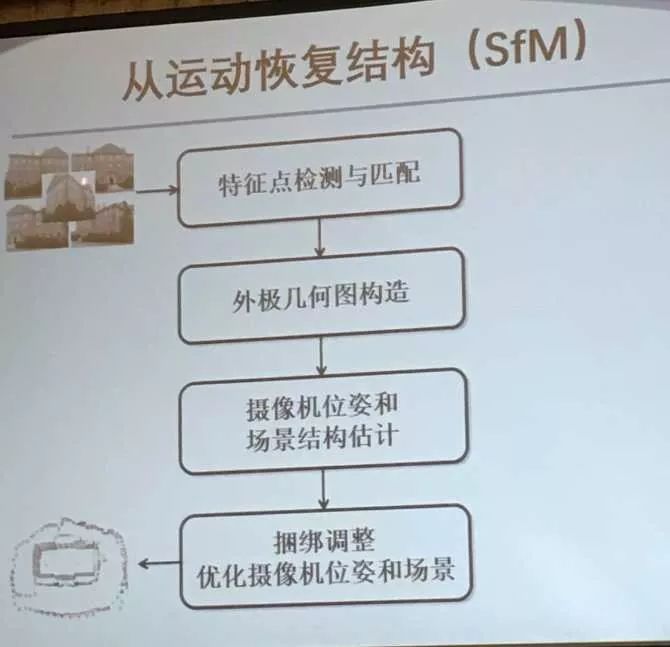
SfM包括以下步骤：

1. 特征点检测与匹配

2. 外极几何图构造

3. 摄像机位姿和场景结构估计

4. 捆绑调整（BA）优化摄像机位姿和场景

特征点检测和匹配：

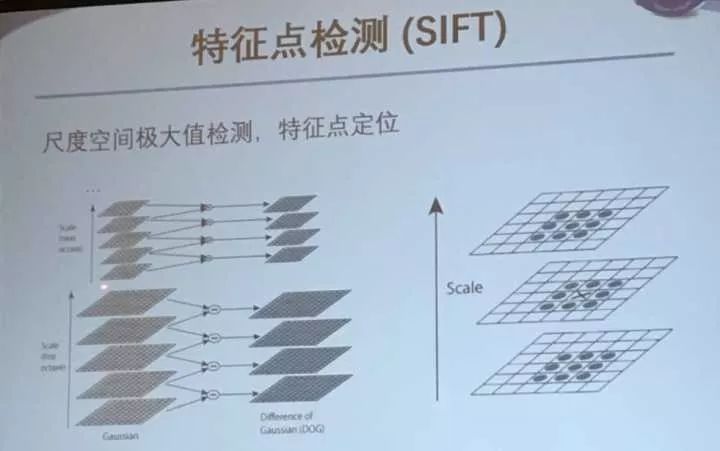
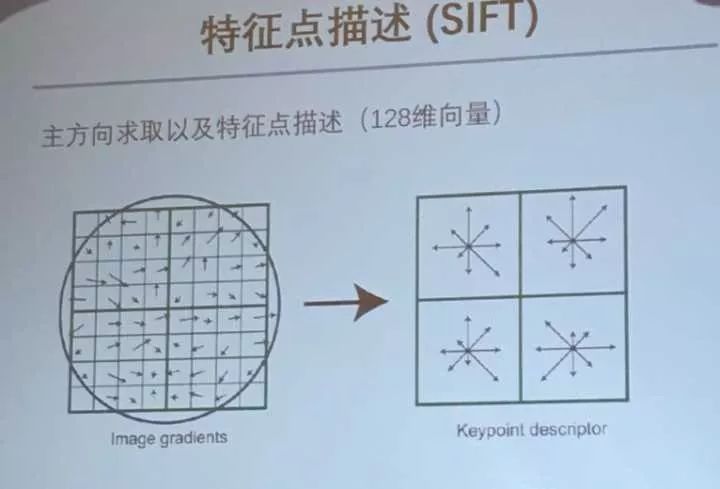
特征点检测用SIFT

特征点匹配：

• L2范数距离最小

• 比值约束：最近邻/次近邻小于一定阈值

• 外极几何约束（匹配特征点在对应的外极线附近）

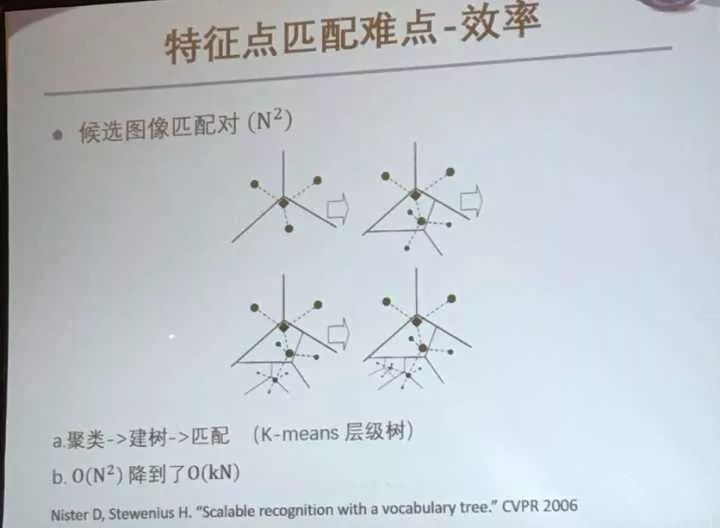
特征点匹配的难度：候选图像匹配对非常多。这里介绍了一篇解决这个问题的论文。

通过聚类、建树、匹配。（K-means层级树）

可以把复杂度降到线性。

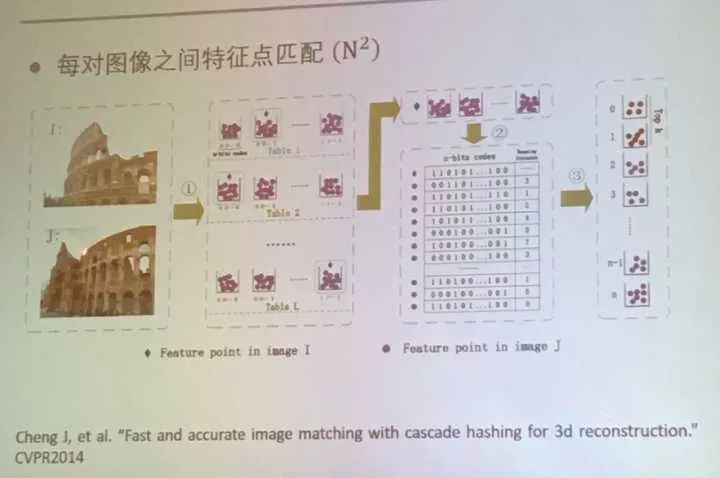
这里介绍了每对图像之间特征点匹配用一个哈希表方法优化的方法。

但是有些地方还存在误匹配问题。极端一点的是如图所示的天坛正反面几乎完全一样。

这里讲了一个用Loop约束来去除错误外极几何关系的方法。

还有一些其他解决方法：

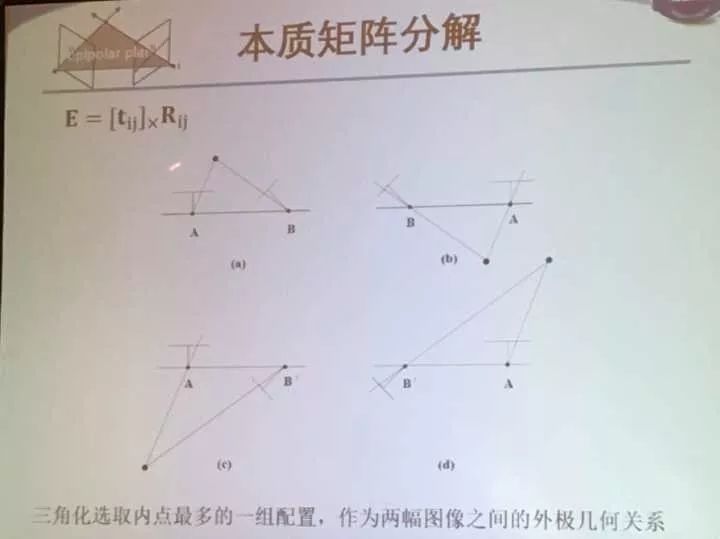
接着讲本质矩阵分解：三角化选择内点最多的一组配置作为外极几何关系。

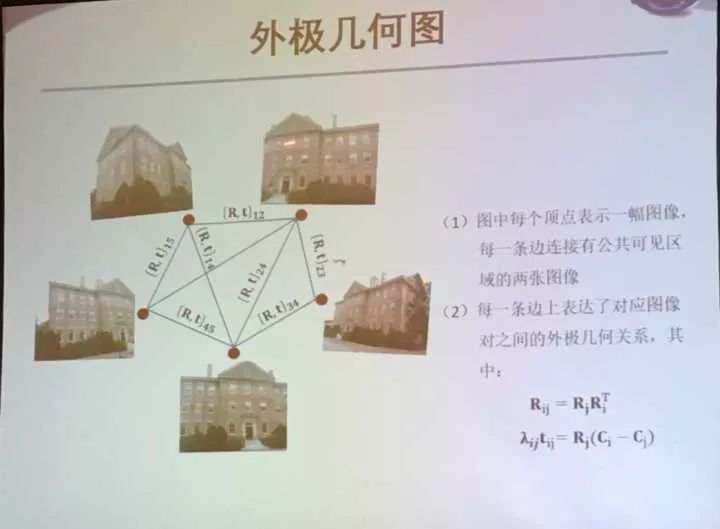
外极几何图构建

3、摄像机位姿和场景结构

包括三种方法：

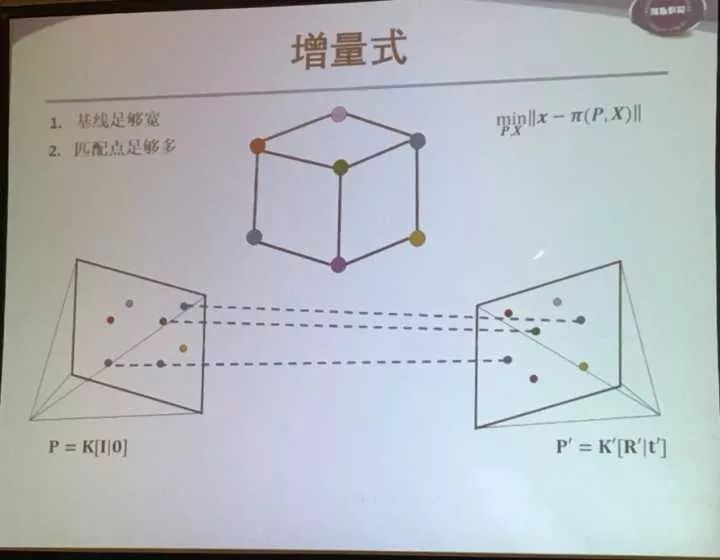
1. 增量式（Incremental）

2. 全局式（Global）

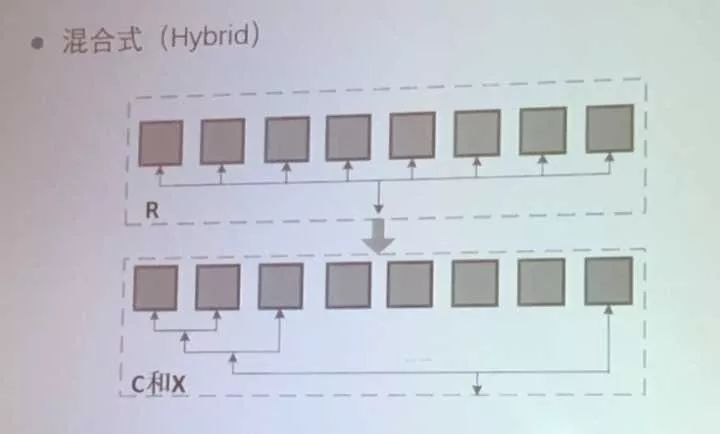
3. 混合式（Hybrid）

增量式要先选择两个图作为初始，一般要求：1.基线足够宽 2.匹配点足够多 当然这两个是矛盾的两个项。通过最小化右边式子来求取。

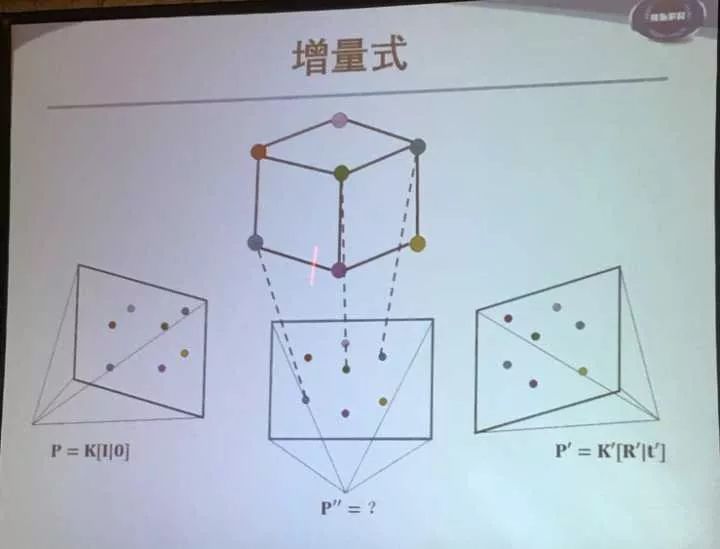
然后开始增加一张图：

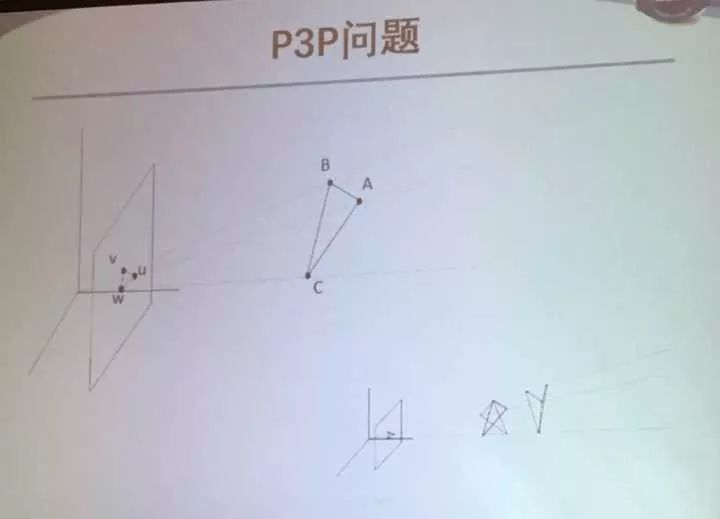
这就变成了P3P问题：

三角化：

捆绑调整：

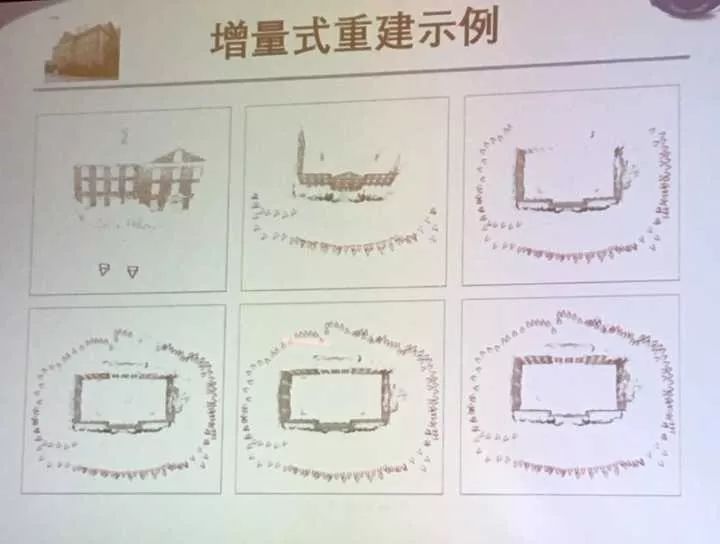
增量式示意图：

3.1、增量式的优缺点

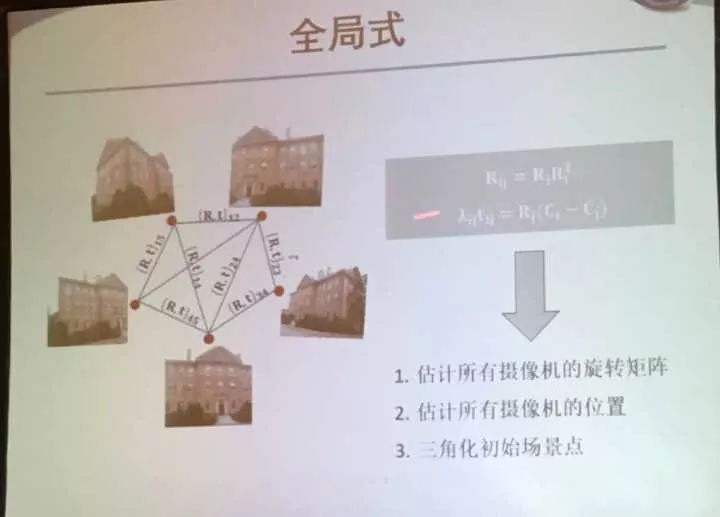
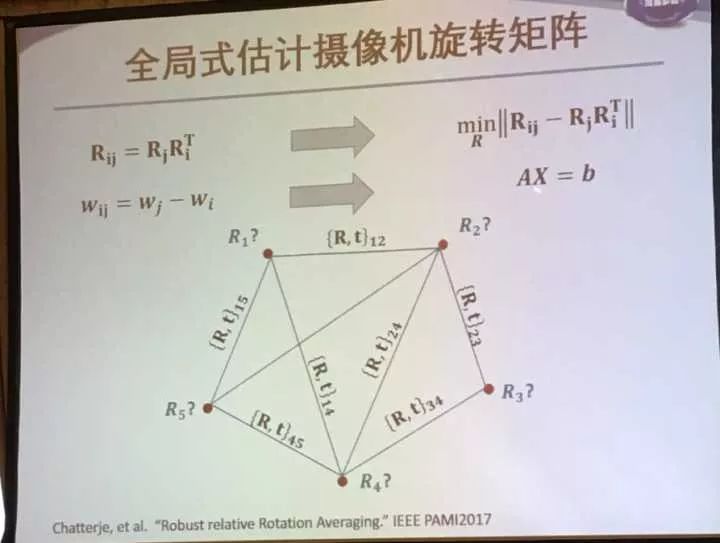
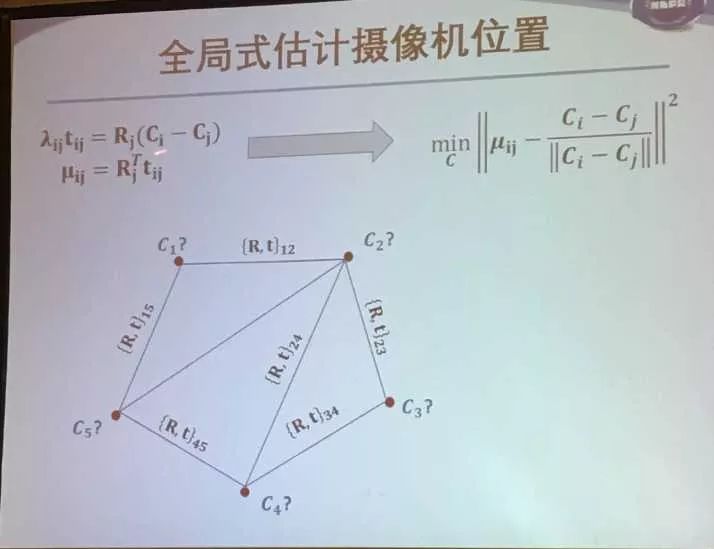
全局式：估计所有摄像机的旋转矩阵和位置并三角化初始场景点

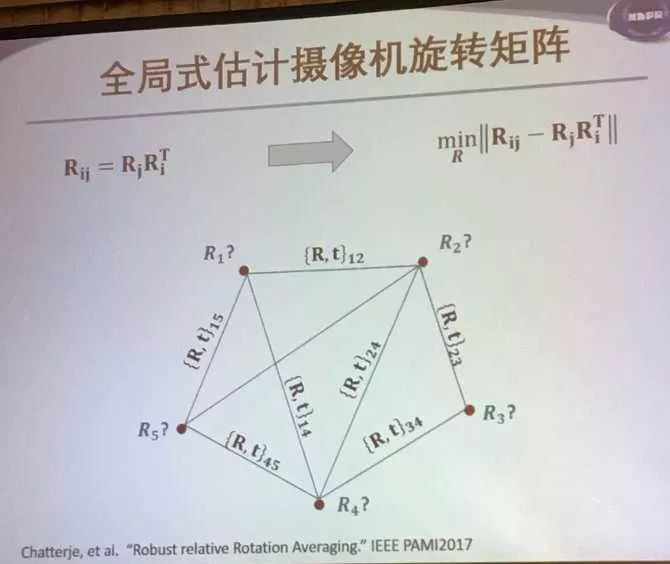
因为经过ij的旋转矩阵要等于Rj和Ri串联之后的结果，所以要最小化两者差的范数作为目标函数。而两个点坐标也应该满足一个关系。

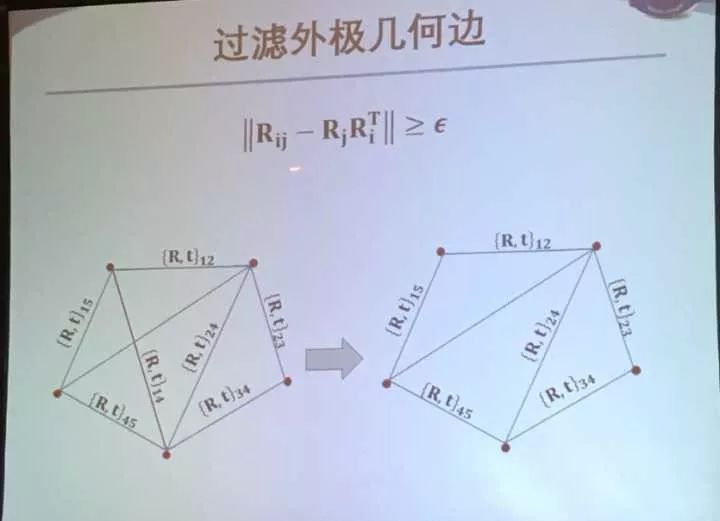
过滤外极几何边：Rij与Rj和Ri乘形成一个范数，要大于一个值

接着推导：目标是让第一项越大越好，让第二项越小越好。

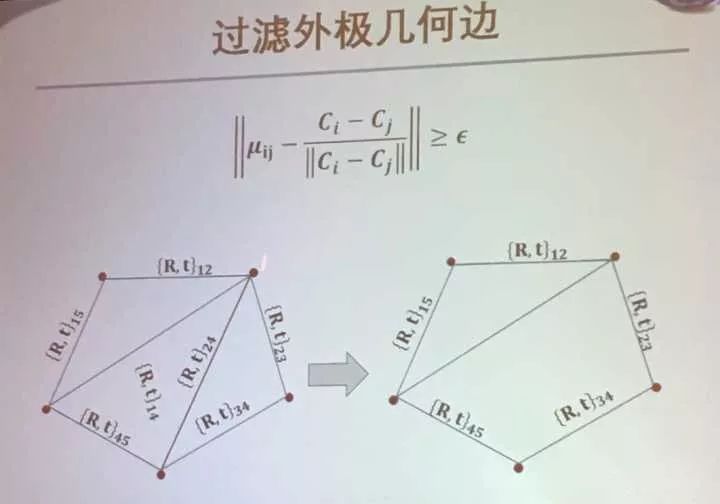
过滤外极几何边：

3.2、全局式的优缺点

相关文献：

比较全局和增量：

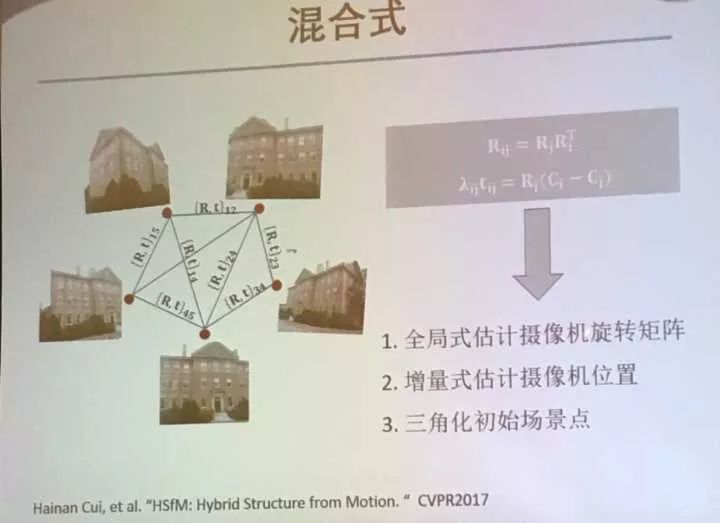
混合式：全局估计旋转矩阵，增量估计摄像机位置，三角化初始场景点。这是CVPR2017的一个工作。

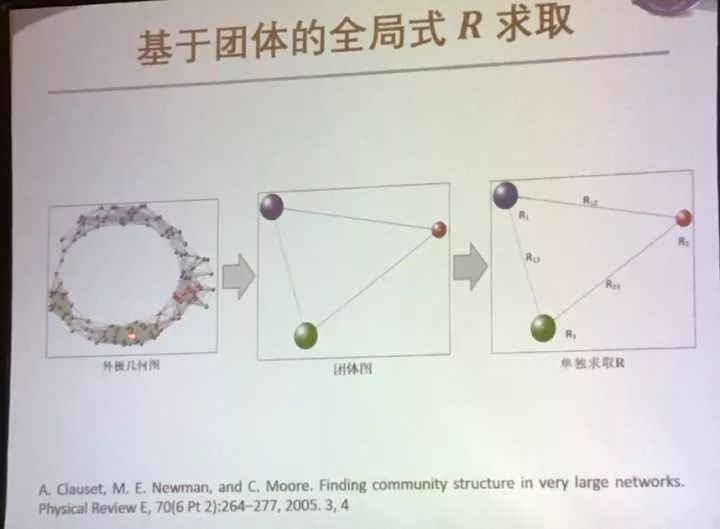
这个方法提出基于团体的全局R求取：先根据相机外极几何图匹配稠密情况把这么多摄像机分成几个团体。

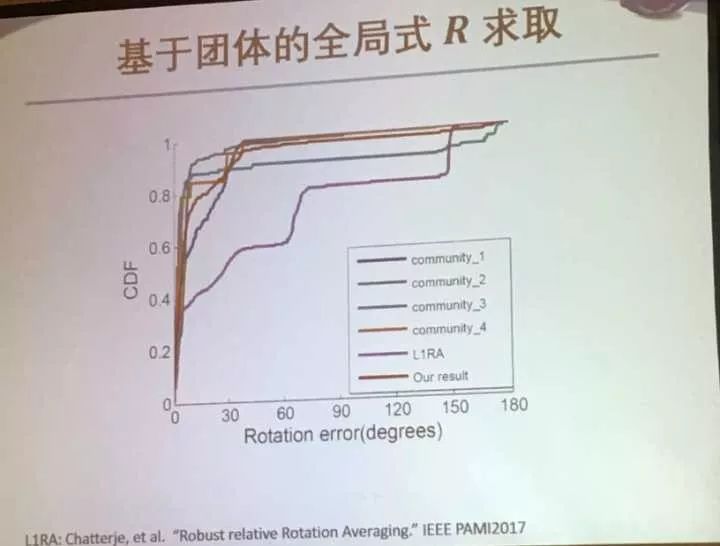
发现这样做有效：

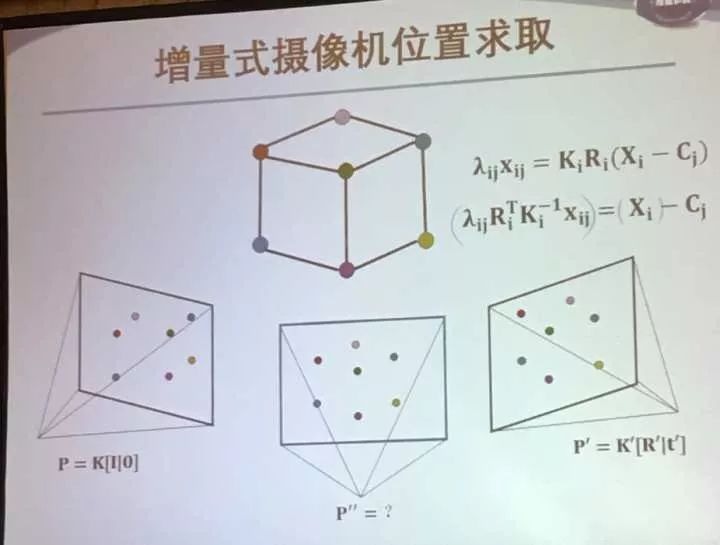
然后用增量式方法求摄像机位置：

求取方法已知旋转矩阵，用两点法求取摄像机位置。有几个优势：

1. RANSAC最小配置减少，更大概率随机到正确的三维点与二维点对应，这样能提高精度

2. 在R已知的情况下，一定程度上可以过滤一部分错误的匹配特征点，这样能提高鲁棒性

3. 每次增量中，可以同时计算得到更多摄像机位置，较少BA次数，提高重建效率

3.3、混合式优缺：

3.4、综合比较：

8、稀疏重建总结

           

—————  AI 科技评论招人啦！  —————

我们诚招学术编辑 1 名（全职，坐标北京）

你即将从事的工作内容：

• 报道海内外人工智能相关学术会议，形成具有影响力的报道内容；

• 采访高校学术青年领袖，输出人工智能领域的深度观点；

• 跟进国内外学术热点，深入剖析学术动态；

我们希望你是这样的小伙伴：

• 英语好，有阅读英文科技网站的习惯；

• 兴趣广，对人工智能有关注及了解；

• 态度佳，有求知欲，善于学习；

欢迎发送简历到 guoyixin@leiphone.com

—————  给爱学习的你的福利  —————

不要等到算法出现accuracy不好、loss很高、模型overfitting时，

才后悔没有掌握基础数学理论！

线性代数及矩阵论， 概率论与统计， 凸优化

AI慕课学院机器学习之数学基础课程即将上线！

扫码进入课程咨询群，组队享团购优惠！

详细了解点击文末阅读原文

————————————————————