留下最重要数学猜想的黎曼

会员服务 ·

留下最重要数学猜想的黎曼

2019 年 3 月 2 日 遇见数学

格奥尔格·弗雷德里希·波恩哈德·黎曼（德语：Georg Friedrich Bernhard Riemann）德国数学家，黎曼几何学创始人，复变函数论创始人之一。

下面部分转自《英才早逝的黎曼》http://episte.math.ntu.edu.tw/articles/mm/mm_04_4_26/index.html, 作者戴久永

英才早逝的黎曼

黎曼(Bernhard Riemann)，乡下牧师的次子，1826年诞生于汉诺威王国的一个小镇。童年时代的他就已显露出对数学的不凡天赋。中学时代，黎曼很幸运地遇到一位善于鉴人的老师，发现他对数学的敏锐领悟力，指导他接近科学的经典作品，所以当他进入大学时，他的学识背景已远超过当时在大学所授各科学科的水准。

黎曼是在1846年，当他十九岁时进入哥廷根大学的，最初专攻神学和哲学，但是不久就获得家人的首肯改习他最热爱的数学。或许由于当时大数学家高斯正是哥廷根大学的数学讲座，使人们对数学水准的低落感到惊异。事实上高斯和其他大多数的德国大学的教授们一样，只是讲授一些基础科目。学生们对教授的权威敬畏有加而很隔阂，教授们也很少给有天赋的学生们嘉勉鼓励。事实上，学生完全没有机会与教师们讨论请益，也不知道教师们如何思考问题。唯一的例外是柏林大学，那里当时正激荡着民主的思潮。同时雅可比（Carl Gustav Jacob Jacobi, 1804～1851）和狄利克雷（Peter Gustav Lejeune Dirichlet, 1805～1859）两位大数学家对相当多的学生讲授他们自己仍然在思考中的题目。黎曼听到这个消息，在哥廷根大学待了一年之后，就前往柏林，在柏林胆怯不爱出风头的黎曼认认了雅可比和狄利克雷，并且非常留心听着两人的热切讨论。狄氏对黎曼非常有好感，黎曼也对狄氏相当敬重。好些黎曼的论文显示狄氏的研究结果对他有重大的影响。在柏林过了两年之后，回到哥廷根，在高斯指导下，完成他的博士论文(1851)。

论文题目是〈Grundlagen fur eine allgemeine Theorie der Function einer verauderlichen complexen Grösse〉，为复变函数理论的一篇基本文献。为了获得成为哥廷根大学讲师的资格，他发表一篇论文〈Über die Darstellbar keit einer Function durch eine trigonometrishe Reihe〉，并且发表试讲，题目是〈Über die Hypothesen welche der Geometrie zu Grunde liegen〉前者是关于三角级数及分析基础，后者则是关于几何基础。前一篇是分析狄黎克雷的将一函数展成傅立业级数的条件，其中条件之一为函数必须为「可积分」。这是什么含意呢？柯西和狄氏都曾经提出一些答案，黎曼则以他自己的定义取代前人对「可积分」所下的定义。他所界定的定义就是我们现在所熟知的「黎曼积分」(Riemann integral)。直到二十世纪，黎曼积分才又进一步地被推广成更具一般性的「拉贝格积分」(Lebesque integral)。后一篇论文的发表逐渐推广了空间的观念，并且于近世导致成为相当广泛且重要的抽象空间的理论。这是由于当时数学界的风尚，重视数学的严密化，同时逐渐趋向于抽象推广化。黎曼对这种现代数学特征的影响比十九世纪的任何一位其他数学家都来得大。

黎曼的博士论文导出「黎曼曲面」(Riemann surface)的概念，转而引进所谓拓朴理念于分析学。在当时，拓朴学可说是几乎完全还没有开发的数学新预域，只有JB Listing于1847年在《Gottinger Stadien》发表过一篇这方面的论文。黎曼证实了拓朴在复变函数理论中的重要性，这篇论文同时澄清了对一复变函数所下的定义。

黎曼于1854年成为哥廷根大学的数学讲师(Privatdozent)，也就是他可以开课，并且向来听讲的学生收费，在这里必须向读者交代一下十九世纪中叶德国的大学的情况。当时科学几乎与国家的经济全然无关。大学的设立仅在训练律师、医师、教师和传教士，以及提供贵族子弟和富家子弟渡过引人侧目及受尊敬的岁月的场所。只有正教授才领有政府的津贴，并且可教授正规标准课程，这些课程都是一些基础科目，上课的学生多，因此教授收到的学费也就多了，这就是为什么课程水准低落的原因，因为如果课程太难，就没有办法收到许多学生，从而影响到教授们的收入，毕竟贵族子弟和富家子弟上大学的目的并非真心向学。讲师们则没有政府津贴并且轮不到教基本正规课程的机会，全然靠来听课的学生的学费维生，通常，听课的学生不会多，因此收入也就相当微薄，生活非常困苦。担任讲师是成为正教授(ordinary professor)的必经途径。但是却无明文规定何时能将一位讲师升等为教授，为了照顾特别值得重视的学者而却没有正教授的空缺时，政府可任命他为「客座教授」:(extra ordinary professor)，使他具有教基本正规课程的资格，增多他的收入，但是这个任命附有条件，言明政府不付任何津贴。

由于黎曼的父亲是个收入微薄的牧师，而且子女众多，自顾尚且不暇。当然在经济上无法帮助地，因此当黎曼决定顺从内心的呼唤，走上了在大学任教的路子，确实有一段日子生活非常困苦。而外在现实环境在他内心也构成重大压力，在他回到哥廷根后十年之间，他全神专注地发展关于复变函数的性质，复变函数在「亚培尔积分」 ( Abelian integral) 理论和「西塔函数」(theta function) 的应用的观念，函数以三角级数的表示法，以及关于几何基础方面的研究，这十年的时间使他建立起科学家的声誉，但是困苦的生活促使他得到肺病，这个病症使他后半生蒙上一层阴影，直到去逝为止。

1855年高斯去逝，狄黎克雷继承高斯的数学讲座的职位。在这个时际，或许是由于狄氏的极力争取，黎曼得到由政府付给的少量薪津，数目仅为正教授所得薪津的十分之一，四年之后，狄氏去世，黎曼被任命为正教授，继承了狄氏的遗缺，这时他是三十三岁，从此他再也不必为经济问题苦恼伤神，但是他的健康情形却因长期工作过度和营养不良而大受损伤。

哥廷根颇为潮湿并且气候不定，为了改变环境，他经常到义大利旅行。那里的气候比较干燥，同时天气情朗，他并且在义大利住过几年。尤其是义大利比萨，在那里他的数学同侪，包括比提(Betti) 和贝特拉米(Beltrami) 非常敬服他的学识，诚心地招待他。

1862年，黎曼和他的朋友的妹妹结婚，1863年，他的女儿诞生于比萨。三年后，也就是1866年七月，黎曼因身体健康恶化，在一个叫Lago Maggiore 地方的小镇去世，年方四十岁。

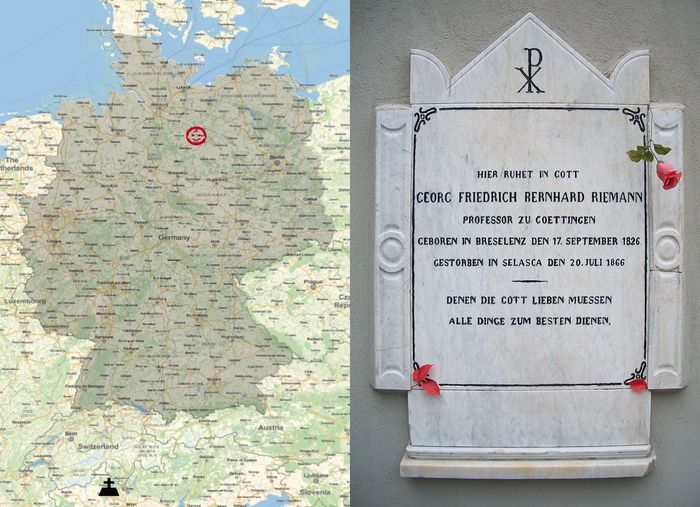
黎曼出生于汉诺威王国（今德国下萨克森）的小镇布列斯伦茨（Breselenz）、葬于意大利皮埃蒙特大区的韦尔巴尼亚 (右图自维基)

Here rests in God Georg Friedrich Bernhard Riemann

Professor in Göttingen

born in Breselenz, 17 September 1826

died in Selasca, 20 July 1866

For those who love God, all things must work together for the best.

这里安息着格奥尔格·弗雷德里希·波恩哈德·黎曼

哥廷根教授

1826年9月17日出生于布雷塞伦茨

1866年7月20日在塞拉斯卡去世

对于那些爱上帝的人来说，所有事情必须一起努力才能做到最好。

黎曼虽英年早逝，但是他所留给数学界的，在他少量的已出版的论文集中，已有太多的丰富的概念，至今还未为后世数学家研究殆尽。他的每一篇论文都具有其重要性，其中有几篇甚至开创了全然崭新的数学领域。

当有人说黎曼是一位纯数学家，事实上，这种说法并不完全正确，虽然他对数学有许多重要的贡献，他对物理和数学在物质世界的应用也相当注意。他也曾写过关于热、光、气体理论、磁、流体力学和音响方面的论文。他曾尝试统一重力和光的理论，以及调查人耳的结构，他对几何基础的研究在于探究确定什么是我们物质空间中绝对可靠的知识。他自己曾说过他对物理定律的研究是他主要的兴趣所在。身为数学家，他自如地利用数学直觉和物理推论。依据Felix Klein 所提供的证据显示，黎曼对复变函数的观念很可能就是来自绝对电流沿着平面流动的研究。事实上，截至上一世纪为止，一个有成就的数学家必定也在应用数学方面有所表现，那时的数学家除了数学中的抽象世界外，他们的脑海中还有一个充满了各种自然现象的真实世界。