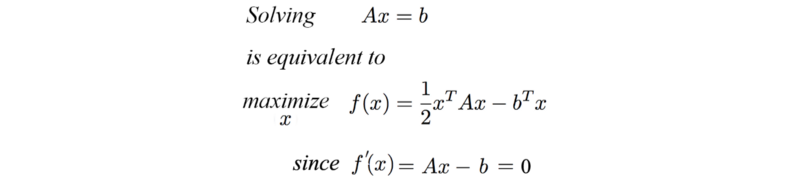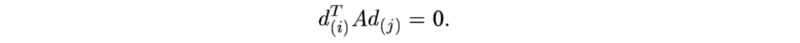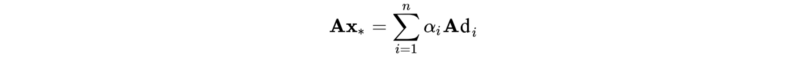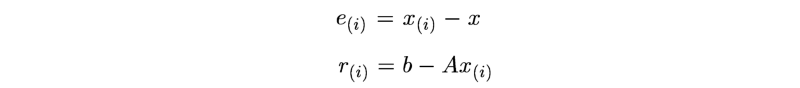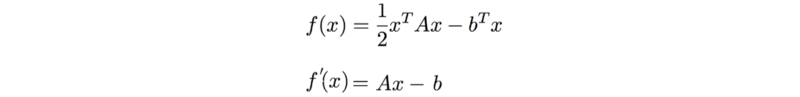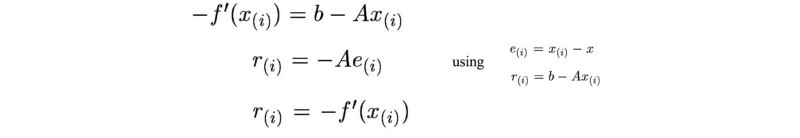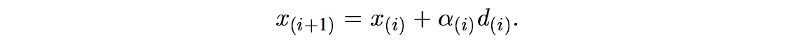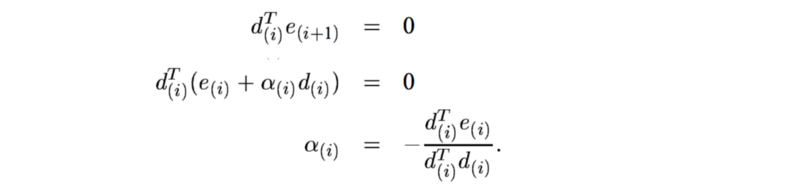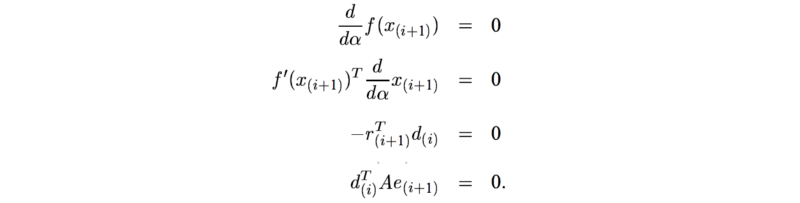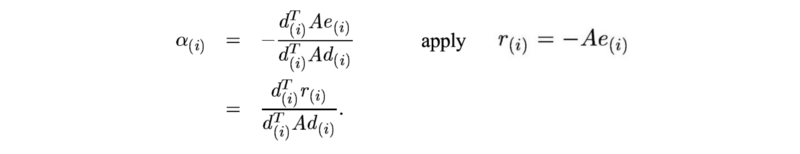强化学习基础 - 共轭梯度

本文为 AI 研习社编译的技术博客，原标题 ：

The base of deep reinforcement learning-Conjugate Gradient

作者 | Jonathan Hui

翻译 | 斯蒂芬•二狗子

校对 | 斯蒂芬•二狗子       审核| 酱番梨      整理 | 菠萝妹

原文链接：

https://medium.com/@jonathan_hui/rl-conjugate-gradient-5a644459137a

注：本文的相关链接请点击文末【阅读原文】进行访问

强化学习基础-共轭梯度

我们可以使用共轭梯度法（conjugate gradient）解线性方程或优化二次方程。并且，针对这两种问题，共轭梯度法比比梯度下降的效果更好。

其中矩阵A是对称正定矩阵

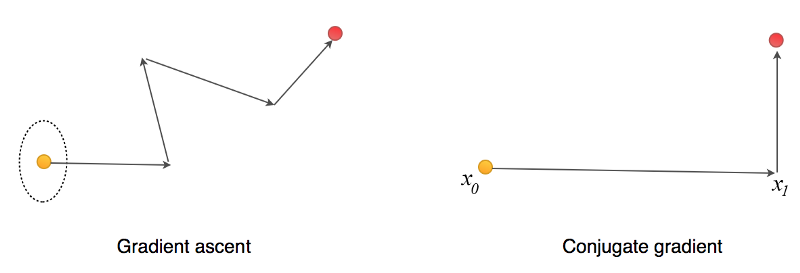
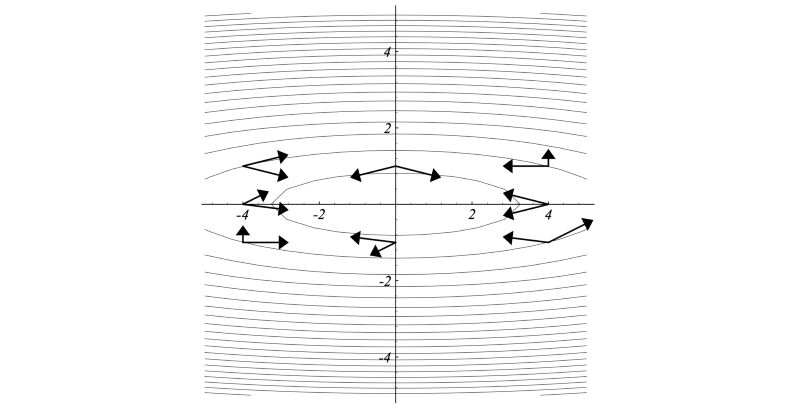
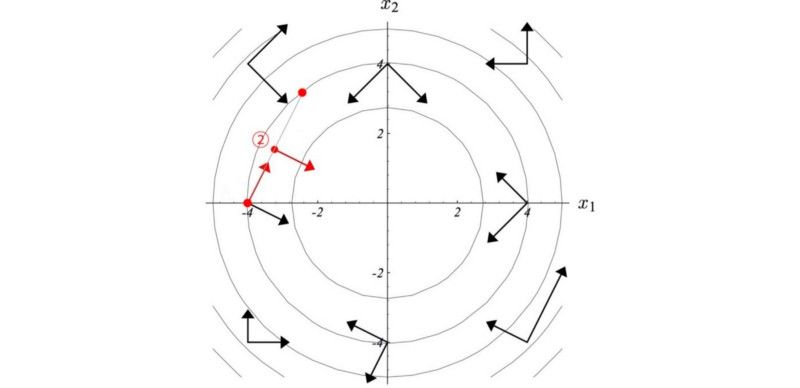
在线搜索方法中，我们确定上升的最陡方向，然后选择步长。举个例子，例如在梯度上升方法中， 我们采用的步长大小等于梯度乘以学习率。看下面左图， 根据梯度的轮廓（用点图圈成椭圆的部分），该点的最大梯度方向是向右的。对应当前点最陡的方向，下一点（迭代）的最陡方向可能是向上并略微偏左。如何我们这次梯度有点微微向左，那么不是给第一步（向右梯度）过程的作用取消了吗？

共轭梯度法是一种线性搜索方法，对于每次的移动，他不会撤销（影响）之前完成的部分。在优化二阶方程上，共轭梯度法比梯度下降需要更少的迭代步数。如果x是N维(N个参数），我们可以在最多N步迭代内找到最优值。因为对于每步移动，希望移动方向与之前的所有的移动方向保存共轭的关系。这一点保证了我们不会撤销所做的移动。简单说，若x是4维的向量，则需要最多4次移动就可以到达最优点。

Modified from source

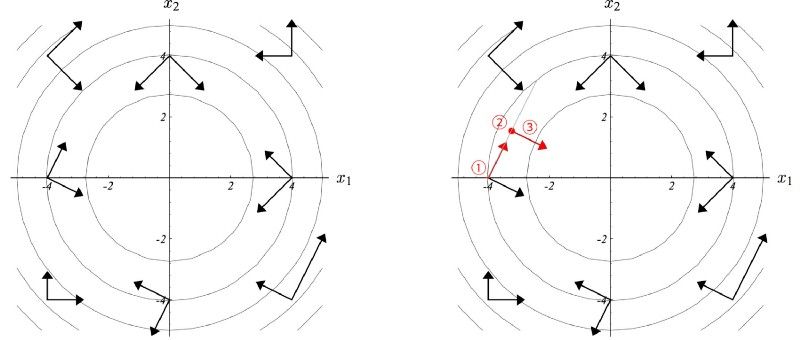
1. 在一个指定的方向做梯度上升

2. 我们在这个方向的最佳点处停下来。

3. 我们找到了一个新方向dj ，它与任何先前的移动方向 di 共轭。

从在数学上来讲，这表示任何新的方向dj 必须与所有 d(i)^TA 共轭，即  

其中A是二次方程的系数矩阵。下面是A共轭（A-conjugate）矩阵在二维空间中的例子。

这些A共轭向量相互之间是独立的。因此，N个A共轭向量可以张成一个N维空间。

该共轭梯度算法（CG）的关键是找到α 和 d。

  共轭梯度算法

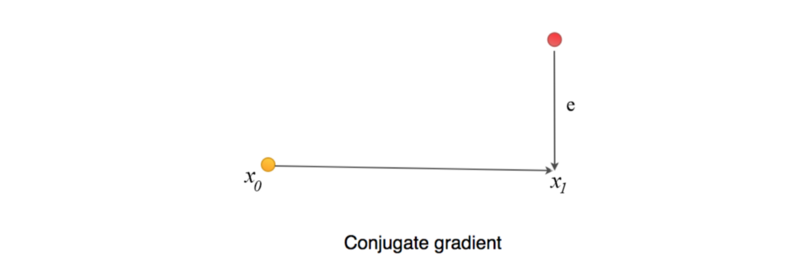
让我先预览一下该算法。我们从一个随机数X(x0)开始猜测问题的解，并计算下一步X1（包括 α 和 d  ）。

d 是下一步移动的方向（共轭向量）。
 让我们看看它的工作原理。首先，我们定义两项：

• e 表示当前猜测点和最佳点之间的误差。

• r 测量的是我们当前值与正确值b（Ax = b）的距离。我们可以把r看成将A投影到b所在空间后与b的误差 e（Ax距离b的距离）。

r,e分别定义为：

函数为

对函数求导

下一个点的计算为（其中α是标量，d是方向，是向量）：

为了保证未来的移动方向不会削减之前移动所做的工作，让我尝试保证e 和 d 是相互正交。也就是，采取该步迭代后的残差应该与当前移动方向保持正交的关系。为了保证之后迭代动作不会消减我们刚刚做的工作，因此保持这种正交关系是有道理的。

因此α取决于e，但我们不知道e的实际值是多少。所以使用其他方法代替正交，让我们尝试另一种猜测（估计方法）。也就是新的搜索方向应与前一个方向正交。 A-orthogonal的定义是：

为了满足这些条件，下一个迭代步的点 xi 必须是搜索方向d上的最佳点。

Modified from source

根据A正交要求时，α计算如下：

Modified from source

wikipedia上的证明:

这里不会完整证明。但有兴趣的人可以看看：

en.wikipedia.org/wiki/Derivation_of_the_conjugate_gradient_method

想要继续查看该篇文章相关链接和参考文献？

长按链接点击打开或点击底部【阅读原文】：

https://ai.yanxishe.com/page/TextTranslation/1428

【点击跳转】强化学习基础-对偶梯度上升

AI研习社每日更新精彩内容，观看更多精彩内容：

盘点图像分类的窍门

动态编程：二项式序列

如何用Keras来构建LSTM模型，并且调参

一文教你如何用PyTorch构建 Faster RCNN

等你来译：

如何在神经NLP处理中引用语义结构 

你睡着了吗？不如起来给你的睡眠分个类吧！ 

高级DQNs：利用深度强化学习玩吃豆人游戏

深度强化学习新趋势：谷歌如何把好奇心引入强化学习智能体 

点击 阅读原文 查看本文更多内容↙