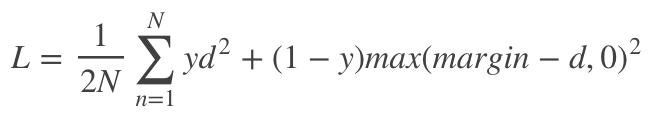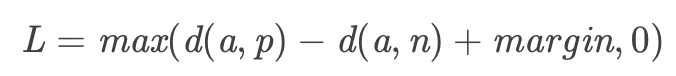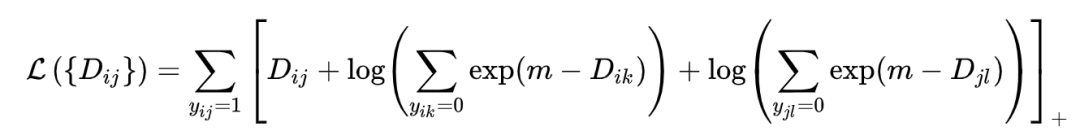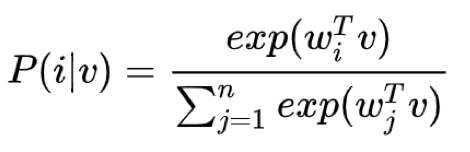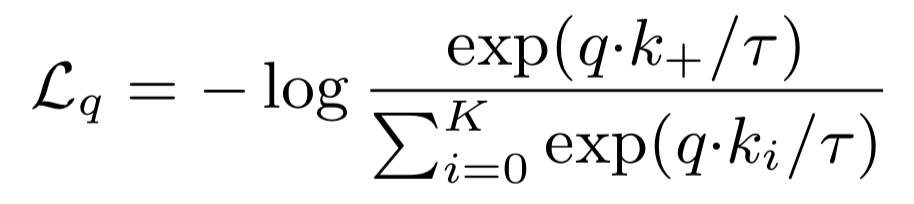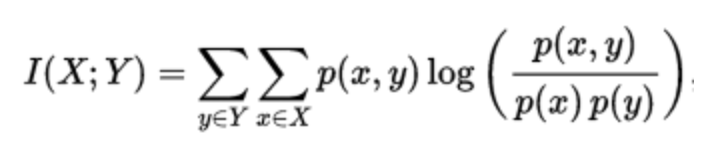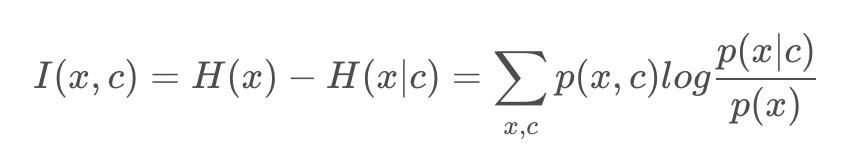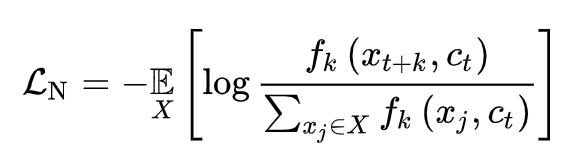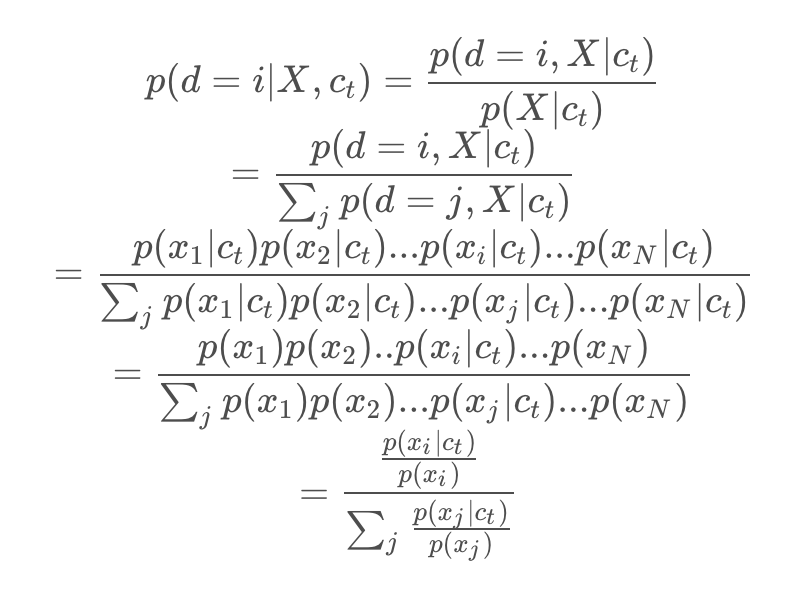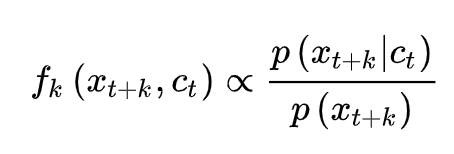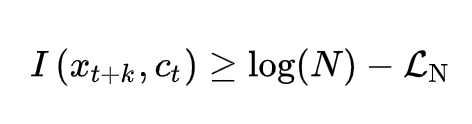Cross-Modal & Metric Learning 跨模态检索专题-3(下)
·前言
专题链接:
Cross-Modal & Metric Learning 跨模态检索专题-1
Cross-Modal & Metric Learning 跨模态检索专题-2
Cross-Modal & Metric Learning 跨模态检索专题-3(上)
本专题计划分3个部分共4篇文章介绍图文跨模态检索的一些工作与思考。第一篇将侧重 "multi-modal" 和 "application", 介绍相关概念与研究背景;第二、三篇会侧重"algorithm" 介绍这个方向研究的技术路线,其中第二篇介绍基于 GAN 的追求公共子空间的 cross-modal 检索;第三篇则从 modal 抽象成更一般的 domain,并且将多域扩展到单域,总结分析单/多域匹配问题,主要介绍基于 contrastive learning / instances discrimination的研究思路。
本篇内容删除了我工作中未公开的信息、也删改了与在投 paper 有关的内容,所以有些地方只能"点到为止"。虽然删减了很多,但是内容实在写的太多了,微信又不支持公式输入,为了提升速度满足同学催更,所以第3篇拆成上、下两篇发出。(早知道就用视频讲了)
本文脉络
(上篇)无监督表示学习与Instances discrimination
(上篇)问题的一般抽象
(上篇)采样的各种花式组合
(下篇)配合采样的各类 Loss 函数
04
—
配合采样的各类 Loss 函数
第3小节介绍了很多采样组合方式,本小节将介绍这些经典的采样可使用的 Loss 函数,同时会从互信息量的角度介绍为什么要增加负样本采样数量。
4.1 二元组常用 loss
对于最常见的二元组采样组合形式,其 pair-wise loss 设计有2类常用的选择。一种是直接基于样本距离大小的函数,一种是在距离 margin 的基础上再拟合一个0/1 label。二者本质一样,前者更加符合 metric learning 的正统血脉,但后者在一些实际应用场景下,由于能够提供一个 score 值,所以反而更常用一些。
第一种中代表性 loss 是 contrastive loss:
其中 d 代表当前 pair 的距离,当y=1,即是正样本对时,我们希望正样本 pair 间距离越小越好最好等于0,所以此时 loss 剩下的 是我们需要优化。当 y=0,即使负样本对时,我们希望二者距离越大越好。大到什么程度呢?这就需要设置一个 margin,当负样本对距离比设置的 margin 小,我们认为模型训练的还不够,需要继续减小这部分 loss 的大小,所以此刻 loss 剩下的是 。当负样本距离已经比 margin 大了,我们认为模型已经可以了,所以 loss=0 无需调整。
第二种的一般做法是,先计算 pair 间距离,然后再经过一层 FC layer,这一层只有2个节点,然后再经过一个激活函数比如 sigmoid 得到需要拟合的0/1值。这里的拟合其实一般当做一个分类了,可以用 cross entropy。给个示例代码:
def inference(cosine_out):with tf.name_scope("DemoInference"):with tf.variable_scope("DemoInference", reuse=reuse):W3 = tf.get_variable(name = "W3", shape=[1,2],initializer=tf.random_normal_initializer(mean=0, stddev=0.1), trainable = True)b3 = tf.get_variable(name = "b3", shape=[2],initializer=tf.random_normal_initializer(mean=0, stddev=0.1), trainable = True)y_hat = tf.nn.xw_plus_b(cosine_out, W3, b3)return y_hat,W3,b3cosine_out = cosine_func(img, word)#获得pair 的cosine 距离y_hat,_,_ = inference(cosine_out)loss_label = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits=y_hat, labels=label_))
4.2 三元组常用 loss
提到三元组的 loss 这一专属名号可以说是非 triplet loss 莫属了, triplet loss 早期是人脸识别里应用的比较多。是在 <anchor,positive,negative> 这样的采样组合中运用距离相关的 loss 来优化模型。也有一些基于此的变种,比如 triplet center loss 等等,但其本质思想都是一样的,让 anchor 与正例positive 之间的距离小于 anchor 与 negative 之间的距离。
上式中,d(a,p) 、d(a,n) 分别表示 anchor 样本与 positive 、negative 样本之间的距离。当 d(a,p) > d(a,n)时,说明 anchor 离正例的距离比到负例的距离还远,此时 loss > 0 需要优化。当 d(a,p) < d(a,n)时,符合 loss 设计的思想,但是这个力度还不够,因此需要再设定一个 margin。让 d(a,p)+margin < d(a,n)时,说明 anchor 与 positive 之间的距离很小,加上一个 margin 后还小于anchor 与 negative 之间的距离,这是我们追求的理想状态,此时 loss=0 无需优化。
专题上半篇中提到 triplet 的采样方式有多种,在实际应用中,按照样本重要性进行加权采样,或者按照 negative 与 anchor 距离最小的准则采样等方式,这些采样技巧对模型的影响也很大。
4.3 Lifted Structure loss
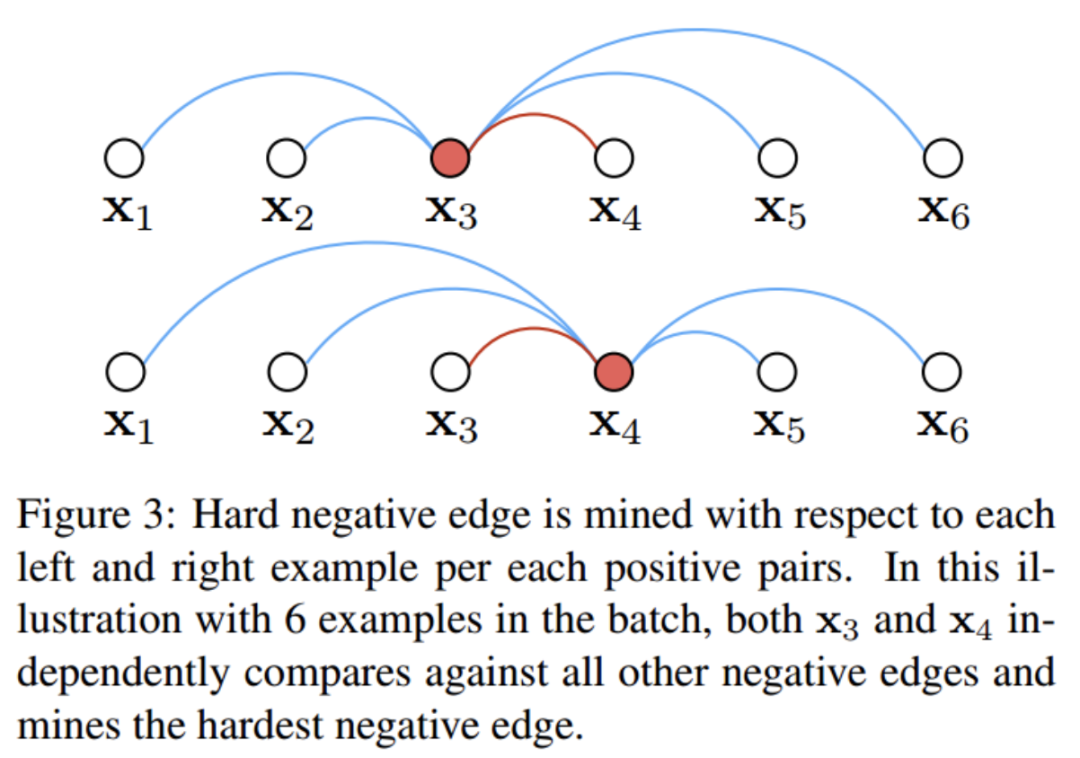
Lifted structure 在采样和 loss 设计上都有改进,采样时考虑了样本的重要性,用了 smooth 的采样方法,同时充分利用 batch-size 内数据得到所有样本对。
对于 和 不区分谁是 anchor,都去搜索难分负例。并且平滑的挑最难的样本,即使用 log-exp 函数来替代传统的 max 操作。
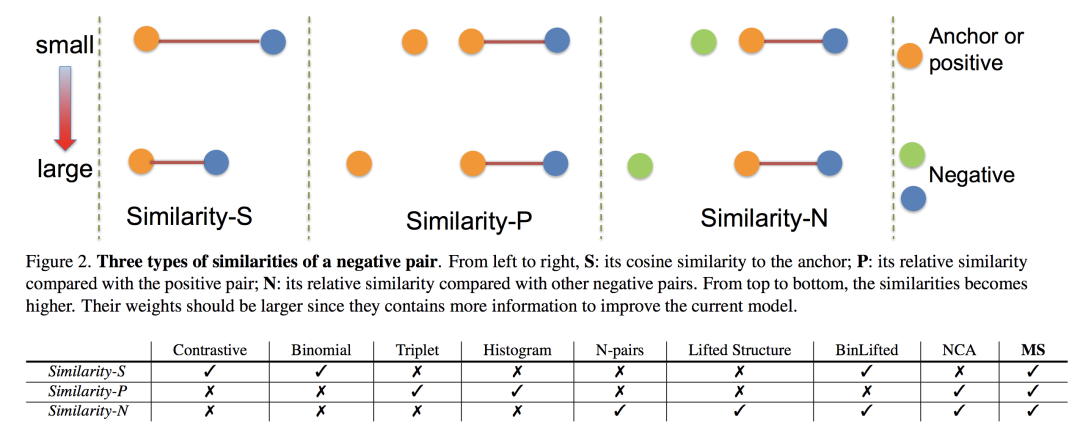
除了上面介绍的这些 loss,还有一些有意思的变种比如 Quadruplet loss、Binomial loss 等等, 最近有一些 metric learning 方向的理论性文章有总结对比这些 loss 的异同,比如19年CVPR的这篇 Multi-Similarity Loss with General Pair Weighting for Deep Metric Learning。文章中分析了上面这些 loss 的优缺点,提出了一个统一的框架 GPW。这里不介绍 GPW,贴一些各个 loss 的对比分析吧:
建议感兴趣同学可以去看一下这篇文章。从3个角度(multi-similarity)对当前常用 loss 做了分析。
4.4 N元组常用 loss
专题上半篇介绍了N 元组的采样,可以在 batch 内部,也可以 beyond batch 扩展到更多的样本,我们这里统称这些模型的 loss 为 infoNCE(N-pair loss、以及 beyond batch 的一些 negative log-likehood loss 都当作这一类)。
N 元组的采样组合形式,天然的就是一个检索场景。给的一个待检索的样本 q,我们从一堆样本中找到一个相关的样本 key,排除其他不相关的样本。不识一般性,我们假设这堆样本候选集大小为 N,其中N-1个是负样本,只有第 i 个是正样本。
如果是一个多分类场景,上面这个任务是可以用典型的 softmax loss 来解决。但是在 instance discrimination 中,这个多分类的类别数可以是所有样本的个数,此时如果还要训练出所有去那种 w,显然是不现实的。
所以我们需要去掉这个 w,希望用一个 Non-parametric 的 loss。有一个方法就是使用样本embedding 自身的转置来代替 w。这样得到一个非参 softmax loss:
同时,可以考虑在多域检索场景下,这个 和 就可以分别代表2个域中的样本。相当于是2个样本先计算内积(也可以换成计算出的 cosine 值),然后通过样本间的内积约束得到 loss。
基于上面的演变,我们以文搜图检索场景为例介绍 infoNCE loss 如下,
上式中 q 代表检索文本的embedding、k 代表被检索的图片embedding、 表示与检索文本 q 相关的图即为正例 pair。这个 Loss 直观的感觉就是和 softmax 很像,但是多了一个超参 ,这个 值一般建议是0.07,当我们把它调到1时,本质就是一个 softmax 了,我个人实验经验0.07这个值确实很合适,再小了很容易数值溢出,太大了效果变差。
对于1正 N-1 负的 N 元组来说,这个 loss 的思想就是对于正例 pair,让二者之间的距离(这里用的内积距离)越小即分子上的内积值越大,分母是所有组合 pair 的距离和包括到所有负样本的距离,所以希望距离越大越好即分母的内积和越小。所以直观的能感受到这个 loss 是符合我们的认知的,希望分子的正例组合相似度变大,分母的负例组合相似度变小。
专题前几篇反复提到这个采样组合 N 的大小(N-1个都是负样本组合数)对模型的影响,这里推导一下证明 N 越大确实会"有帮助"。
首先介绍互信息。两个变量的互信息是变量间相互依赖性的量度,互信息用来度量两个事件集合之间的相关性。它度量 X 和 Y 共享的信息,比如知道其中一个变量后,对另一个变量不确定度减少的程度。当 X 和 Y 相互独立,则 X 的存在对 Y 不提供任何信息,此时互信息为 0。X 和 Y 的互信息数学定义如下,我们只考虑离散变量(连续变量时,就是积分形式):
上式中 p(x,y) 是联合概率密度函数,p(x)、p(y)分别是 X 和 Y 的边缘概率密度函数。互信息与边缘熵 H 有下面的关系: I(X;Y) = H(Y) – H(Y|X) ;熵 H(Y) 表示随机变量Y不确定度, H(Y|X) 就是 X 已知后 Y 的剩余不确定度的量。
理解了上面的定义,就可以继续往下了。回到检索场景下,infoNCE loss 的分子就是相关的正样本 pair,分子是一堆负样本。计算检索文本 c,与相关的图片 x 的互信息为:
我们的目的当然是最大化当前检索文本 c 和正例 x 之间的互信息。那么 infoNCE loss 是不是能保证我们的目标呢?我们先把上面的 infoNCE loss 写成下面的形式
实际上一毛一样,用 f 表示上面的 exp 函数,上面 当做是文本 anchor,假设第 i 个是正样本。给定 ,中 采样自p(x),是不相关的负样本,而 采样于 ,是正样本。当我们想从这一堆 X 样本中找到第 i 个即正例的概率是:
当我们优化 infoNCE loss 时,从二者形式也能看出来就是在最大化 是一个正样本的概率。
这里我主要是基于 CPC 这篇文章中的理论 Representation Learning with Contrastive Predictive Coding 来介绍,最终得到的结论就是:
所以,虽然直接优化 x和 c 的互信息很难,但是可以通过优化 infoNCE loss来提高二者互信息的下界,一定范围内 N 越大效果越好。实际实验来看,增加 batch-size 大小,以及超出 batch-size 获得更多的负样本 pair,模型效果是会变好的。
这里的数学理论比较多,很久前看的了,我现在也忘记的差不多了。。。所以可能存在一些错误,欢迎反馈指导。
4.5 实际应用中&未来优化方向的一些思考
1)对偶思路。在 N 元组采样方式下,我们都是默认了只有一个 anchor,比如一词采样多个图。但实际上图与文并没有角色上的区别,即使最终任务是开发一个文本搜图系统,训练时也是可以用图片当 anchor 配多个文本的采样方式。因此一个 batch 内部,构造出一文多图的 N-pari,同时也构造出一图多文的 N-pair,2个 loss 一起优化。
2)更有效的采样。比如加权采样、难分样本挖掘等。虽然采样的数量 N 越大效果会越好,但是N 达到一定范围后,效果就基本没有提升了。因为随机采样的负样本,多到一定程度后,再多的都是那些远离边界的样本,提供的信息很有限。因此需要考虑如果采样更重要的负样本。这里建议看下 GPW 文章,有助于对采样重要性有更深的理解。
3)结合 GAN 等思路,继续创新loss 设计。这个是对偶思路的升级版,不妨更大胆一点,打破跨模态的壁垒,不用区分图还是文,全都一视同仁。这样采样的方式就更多了,结合 GAN loss 一起,会达到更好的效果。这里我们也在做相关投稿工作,就不说太多了。
4)去掉枷锁,实事求是。脱离了具体任务的指导方针都是危险的,还是需要在实际的任务中,充分了解数据的分布特性,设计合理高效的采样方式和 loss 函数。
后记
专题终于写完了!"太长不看",以后写短篇吧。。。
推荐阅读
斯坦福大学NLP组Python深度学习自然语言处理工具Stanza试用
太赞了!Springer面向公众开放电子书籍,附65本数学、编程、机器学习、深度学习、数据挖掘、数据科学等书籍链接及打包下载
数学之美中盛赞的 Michael Collins 教授,他的NLP课程要不要收藏?
模型压缩实践系列之——bert-of-theseus,一个非常亲民的bert压缩方法
关于AINLP
AINLP 是一个有趣有AI的自然语言处理社区,专注于 AI、NLP、机器学习、深度学习、推荐算法等相关技术的分享,主题包括文本摘要、智能问答、聊天机器人、机器翻译、自动生成、知识图谱、预训练模型、推荐系统、计算广告、招聘信息、求职经验分享等,欢迎关注!加技术交流群请添加AINLPer(id:ainlper),备注工作/研究方向+加群目的。