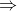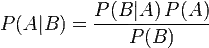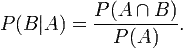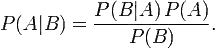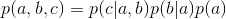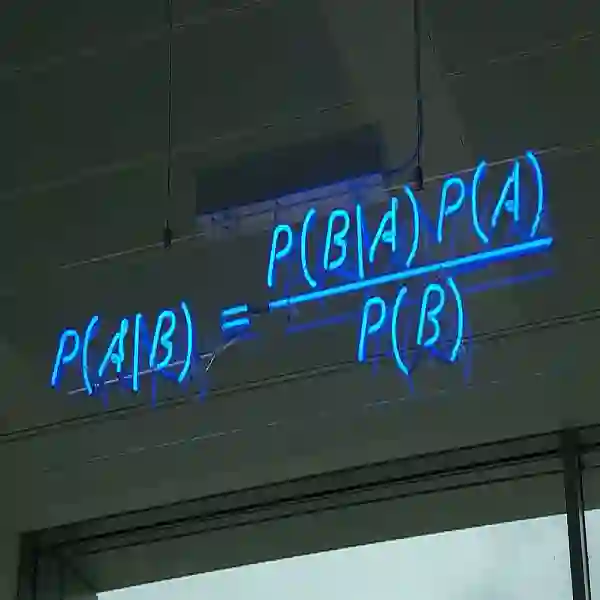从贝叶斯方法谈到贝叶斯网络

2017 年 7 月 6 日 七月在线实验室

引言

事实上，介绍贝叶斯定理、贝叶斯方法、贝叶斯推断的资料、书籍不少，比如《数理统计学简史》，以及《统计决策论及贝叶斯分析 James O.Berger著》等等，然而介绍贝叶斯网络的中文资料则非常少，中文书籍总共也没几本，有的多是英文资料，但初学者一上来就扔给他一堆英文论文，因无基础和语言的障碍而读得异常吃力导致无法继续读下去则是非常可惜的（要想全面了解贝叶斯理论，可点击文末 阅读原文 直达链接）。

贝叶斯方法

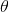
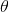
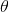
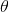
长久以来，人们对一件事情发生或不发生的概率，只有固定的0和1，即要么发生，要么不发生，从来不会去考虑某件事情发生的概率有多大，不发生的概率又是多大。而且概率虽然未知，但最起码是一个确定的值。比如如果问那时的人们一个问题：“有一个袋子，里面装着若干个白球和黑球，请问从袋子中取得白球的概率是多少？”他们会想都不用想，会立马告诉你，取出白球的概率就是1/2，要么取到白球，要么取不到白球，即θ只能有一个值，而且不论你取了多少次，取得白球的概率θ始终都是1/2，即不随观察结果X 的变化而变化。

贝叶斯及贝叶斯派提出了一个思考问题的固定模式：

先验分布 + 样本信息后验分布

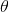
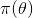
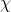
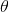
上述思考模式意味着，新观察到的样本信息将修正人们以前对事物的认知。换言之，在得到新的样本信息之前，人们对的认知是先验分布，在得到新的样本信息后，人们对的认知为。

其中，先验信息一般来源于经验跟历史资料。比如林丹跟某选手对决，解说一般会根据林丹历次比赛的成绩对此次比赛的胜负做个大致的判断。再比如，某工厂每天都要对产品进行质检，以评估产品的不合格率θ，经过一段时间后便会积累大量的历史资料，这些历史资料便是先验知识，有了这些先验知识，便在决定对一个产品是否需要每天质检时便有了依据，如果以往的历史资料显示，某产品的不合格率只有0.01%，便可视为信得过产品或免检产品，只每月抽检一两次，从而省去大量的人力物力。

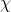
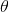
而后验分布一般也认为是在给定样本的情况下的条件分布，而使达到最大的值称为最大后验估计，类似于经典统计学中的极大似然估计。

综合起来看，则好比是人类刚开始时对大自然只有少得可怜的先验知识，但随着不断观察、实验获得更多的样本、结果，使得人们对自然界的规律摸得越来越透彻。所以，贝叶斯方法既符合人们日常生活的思考方式，也符合人们认识自然的规律，经过不断的发展，最终占据统计学领域的半壁江山，与经典统计学分庭抗礼。

此外，贝叶斯除了提出上述思考模式之外，还特别提出了举世闻名的贝叶斯定理。

贝叶斯定理

贝叶斯定理便是基于下述贝叶斯公式：

上述公式的推导其实非常简单，就是从条件概率推出。

根据条件概率的定义，在事件B发生的条件下事件A发生的概率是

同样地，在事件A发生的条件下事件B发生的概率

整理与合并上述两个方程式，便可以得到：

接着，上式两边同除以P(B)，若P(B)是非零的，我们便可以得到贝叶斯定理的公式表达式：

所以，贝叶斯公式可以直接根据条件概率的定义直接推出。即因为P(A,B) = P(A)P(B|A) = P(B)P(A|B)，所以P(A|B) = P(A)P(B|A) / P(B)。

贝叶斯网络

贝叶斯网络(Bayesian network)，又称信念网络(Belief Network)，或有向无环图模型(directed acyclic graphical model)，是一种概率图模型，于1985年由Judea Pearl首先提出。它是一种模拟人类推理过程中因果关系的不确定性处理模型，其网络拓朴结构是一个有向无环图(DAG)。

贝叶斯网络的有向无环图中的节点表示随机变量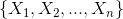，它们可以是可观察到的变量，或隐变量、未知参数等。认为有因果关系（或非条件独立）的变量或命题则用箭头来连接。若两个节点间以一个单箭头连接在一起，表示其中一个节点是“因(parents)”，另一个是“果(children)”，两节点就会产生一个条件概率值。

总而言之，连接两个节点的箭头代表此两个随机变量是具有因果关系，或非条件独立。

例如，假设节点E直接影响到节点H，即E→H，则用从E指向H的箭头建立结点E到结点H的有向弧(E,H)，权值(即连接强度)用条件概率P(H|E)来表示，如下图所示：

简言之，把某个研究系统中涉及的随机变量，根据是否条件独立绘制在一个有向图中，就形成了贝叶斯网络。其主要用来描述随机变量之间的条件依赖，用圈表示随机变量(random variables)，用箭头表示条件依赖(conditional dependencies)。

令G = (I,E)表示一个有向无环图(DAG)，其中I代表图形中所有的节点的集合，而E代表有向连接线段的集合，且令X = (Xi)i ∈ I为其有向无环图中的某一节点i所代表的随机变量，若节点X的联合概率可以表示成：

对于任意的随机变量，其联合概率可由各自的局部条件概率分布相乘而得出：

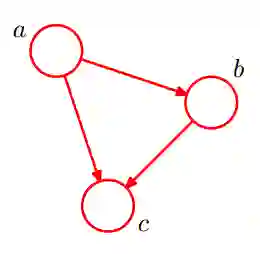
如下图所示，便是一个简单的贝叶斯网络：

因为a导致b，a和b导致c，所以有

贝叶斯网络的实例

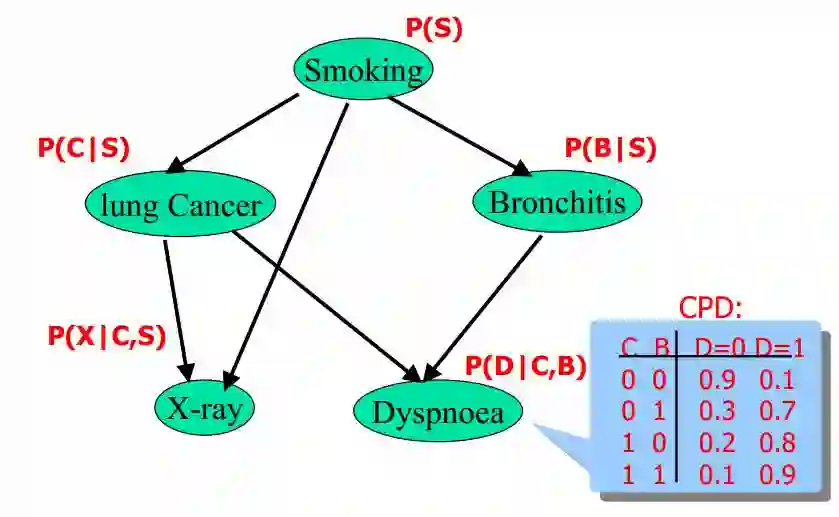
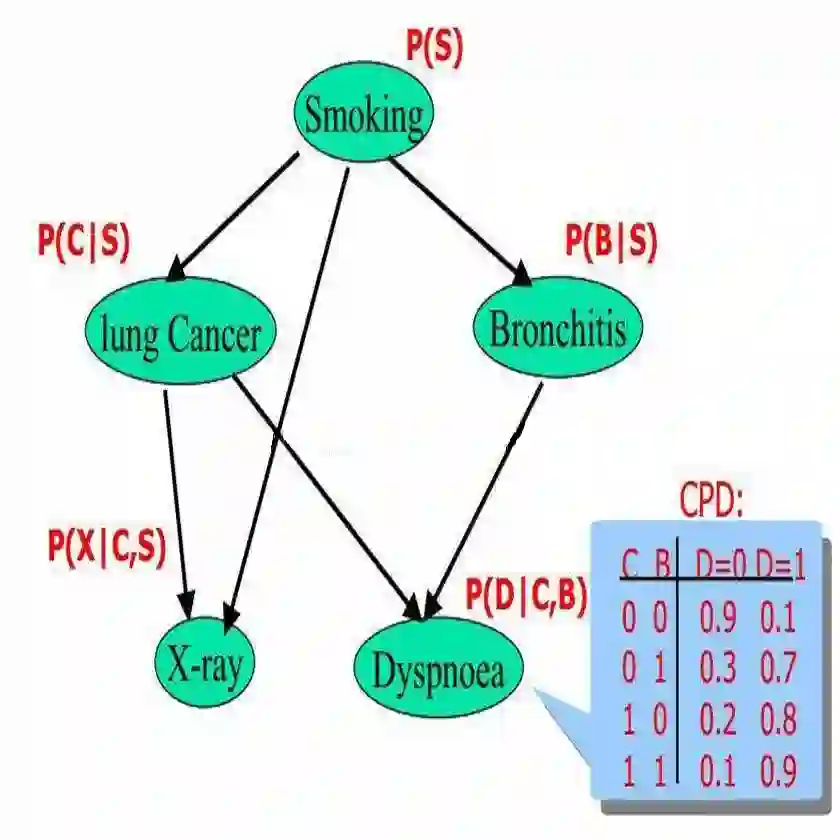
给定如下图所示的贝叶斯网络：

其中，各个单词、表达式表示的含义如下：

smoking表示吸烟，其概率用P(S)表示，lung Cancer表示的肺癌，一个人在吸烟的情况下得肺癌的概率用P(C|S)表示，X-ray表示需要照医学上的X光，肺癌可能会导致需要照X光，吸烟也有可能会导致需要照X光（所以smoking也是X-ray的一个因），所以，因吸烟且得肺癌而需要照X光的概率用P(X|C,S)表示。
Bronchitis表示支气管炎，一个人在吸烟的情况下得支气管炎的概率用P(B|S)，dyspnoea表示呼吸困难，支气管炎可能会导致呼吸困难，肺癌也有可能会导致呼吸困难（所以lung Cancer也是dyspnoea的一个因），因吸烟且得了支气管炎导致呼吸困难的概率用P(D|C,B)表示。

lung Cancer简记为C，Bronchitis简记为B，dyspnoea简记为D，且C = 0表示lung Cancer不发生的概率，C = 1表示lung Cancer发生的概率，B等于0（B不发生）或1（B发生）也类似于C，同样的，D=1表示D发生的概率，D=0表示D不发生的概率，便可得到dyspnoea的一张概率表，如上图的最右下角所示。

猛戳 阅读原文 了解全部贝叶斯理论内容