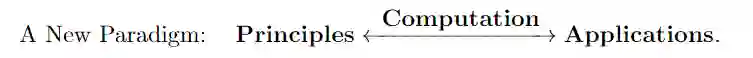荐书｜马毅教授7年力作，稀疏模型教科书正式上架，中文版预计明年问世

---

  新智元报道  

编辑：LRS

【新智元导读】马毅教授七年磨一剑的新书最近上架亚马逊，开售即夺得best seller，马上就要抢光啦！书中系统性地介绍了稀疏低秩低维模型，也是多门高维数据计算原理课程的教科书。

数据科学和机器学习从哪里来，又该到哪里去？

 

稀疏大模型可能是一个答案。

 

稀疏模型在深度学习领域发挥着越来越重要的作用，对于输入只激活模型中的一小部分，从而在大参数量情况下也能做到计算友好；并且特征数够多，可以在广泛的空间中寻找到低维有效信息，所以稀疏模型也具有更好的鲁棒性。

 

马毅教授也称之为「来自高维度的恩赐」，包括谷歌Jeff Dean等都认为这是一个未来趋势，开始宣扬稀疏大模型，重回简约原理的王道上。

 

 

2020年12月，马毅教授官宣了与John Wright耗时七年合著的新书《用低维模型做高维数据分析：原理，计算和应用》，及时地对稀疏低秩低维模型提供了全面系统严格的介绍。

 

书中涵盖了高维数据分析的新数学（统计学、几何学、计算学）原理，具有可扩展的优化方法及其在科学成像、宽带通信、人脸识别、三维视觉和深度网络等重要实际问题中的应用。

 

马毅教授还公开提供了pre-production版本可以在线下载。

 

 

最近新书由剑桥大学出版社出版，在亚马逊上架，一经发售也是夺得了「信号处理」领域的best seller，在计算机视觉和模式识别也排进了前三。

 

 

马毅教授表示，由于书中大部分都是理论，新书的畅销也表示不少人还是关心基础数理与计算原理的，这也应该是将来机器学习人工智能领域学生真正的核心竞争力。并且新书正在由机械工业出版社翻译中文版，争取明年能问世！

 

 

这本书也是数据科学、信号处理、优化和机器学习领域的入门级研究生教材，已经被用于 EECS 290（加州大学伯克利分校）和 ELEN 6886（哥伦比亚大学）两门课程。

 

伯克利大学还因此开设了高维数据计算原理的新研究生课EECS 208，在新书网站上也有课程的全部课件。

 

 

马毅教授于1995年获得清华大学自动化与应用数学双学士学位，后求学于美国伯克利加州大学，并于1997年获EECS硕士学位，2000年获数学硕士学位与EECS博士学位。毕业后在美国伊利诺伊大学香槟分校任教，并成为该校电气与计算机工程系历史上最年轻的副教授。2009年任微软亚洲研究院视觉计算组高级研究员。2014年全职加入上海科技大学信息科学与技术学院。2018年加入伯克利加州大学和清华-伯克利深圳学院，目前是加利福尼亚大学伯克利分校电子工程与计算机科学系教授，同时也是IEEE Fellow，ACM Fellow，SIAM Fellow。

 

马毅教授的研究兴趣包括 3D 计算机视觉、高维数据的低维模型、可扩展性优化和机器学习，近来的研究主题包括大规模 3D 几何重构和交互以及低维模型与深度网络的关系。

 

 

John Wright 现为哥伦比亚大学电气工程系副教授。2009 年 10 月，他取得了伊利诺伊大学香槟分校的电气工程博士学位，2009 年至 2011 年在微软研究院工作。他的研究兴趣在于高维数据分析、信号处理、计算机视觉和优化领域。正在开发用于稳健分析高维数据的工具，并将其应用于视觉数据分析的问题，如图像和视频压缩、人脸和物体识别。这项工作特别强调找到即使在数据不可靠，即有噪音或被破坏的情况下也能表现良好的方法，并且有正确性的证明。

 

 

二位作者曾合作发表的论文至今引用量高达1.1万，已成稀疏表示和计算机视觉领域的经典。

 

 

书籍简介

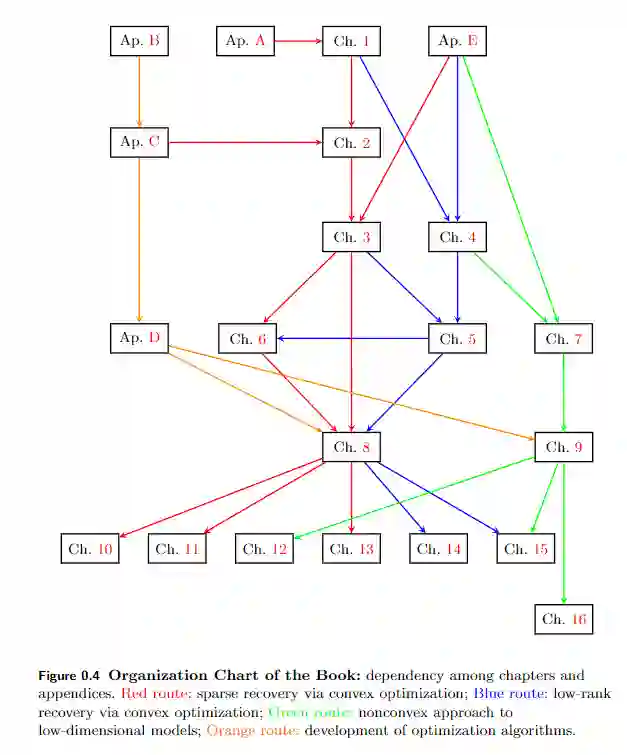
全书共计16 章节，篇幅达730页，相关的背景知识放在了5个附录中。书中的主要内容包括三个部分：原理（Principles）、计算（Computation）和应用（Applications）。

 

原理（2-7章），包含稀疏、低秩、通用低维模型的基本属性和理论结果。这部分表述了恢复低维结构的逆问题变得易于处理，并且能够被有效解决所需的条件，并保证了正确性和准确率。

 

计算（8-9章），介绍了凸优化和非凸优化的方法，以开发适用于恢复低维模型的实用算法。这些方法展示了如何系统地提高算法效率并降低总体计算复杂度，从而使生成的算法快速且可扩展至大规模高维数据。

 

应用（10-16章），展示了原理和计算如何显著改善各种实际问题和事件的解决方案。这些应用也为如何适当自定义和扩展书中介绍的理想模型和算法提供了指导，以将应用和其他特定领域知识（先验或约束）结合起来。

 

附录A-E涵盖了线性代数、优化和高维统计中的基础的数学概念和结果。

 

 

本书的目的

在过去的二十年里，高维空间中的低维结构研究有了爆炸性的进展。

 

在很大程度上，一些代表性的低维模型（如稀疏和低秩及其变体和扩展）的几何和统计特性已经被充分研究并理解。研究人员已经知道在何种条件下可以有效地从（最小量的采样）数据中恢复出来这类模型，并且开发出许多高效和可扩展的算法用于从高维数据中恢复低维模型。

 

这些算法的工作条件、数据和计算的复杂性也得到了彻底且精确的描述，这些新的理论成果和算法已经彻底改变了数据科学和信号处理的实践方法，并对传感、成像和信息处理产生了重大影响。它们极大地推动了科学成像、图像处理、计算机视觉、生物信息学、信息检索和机器学习等领域中许多应用的技术水平。

 

但正如书中所介绍的应用中看到的那样，其中一些发展似乎违背了传统的智慧。

 

作为这些历史性进步的见证者，我们相信现在时机已经成熟，可以对这个新的知识体系进行全面的综述，并在一个统一的理论和计算范式下对这些丰富的成果进行整理。关于这个主题，现有的一些书籍已经关注到压缩传感和稀疏/低维建模的数学/统计原理。

 

然而，本书的目标是通过真正的可操作和可扩展的计算来弥补低维模型在高维数据分析中的原理和应用之间的差距。

 

 

因此，本书不仅建立了对低维结构建模的数学原理，并理解了它们恢复的限制，还展示了如何系统地开发可证明有效和可扩展的算法来解决恢复问题，包括优化领域的经典和最新研究进展。

 

此外，通过大量的科学和技术领域的示例应用，本书旨在进一步指导读者和学生如何处理外部领域知识或其他非理想的因素（如非线性），以正确应用这些新的原则和方法来模拟现实世界的数据，并成功解决现实世界的问题。

 

尽管本书所介绍的应用不可避免地带有作者自己在实践这些一般原则和方法时的专业知识和经验的偏见，但它们是经过精心挑选过的，以传达我们所学到的不同且互补的教训（往往是以一种艰难的方式）。我们相信这些经验对理论家和实践者都有价值。

参考资料：

https://book-wright-ma.github.io/