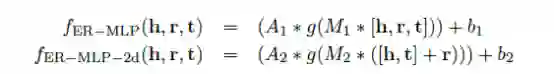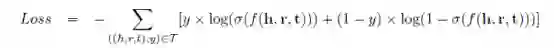【论文读书笔记】重新考虑用简单神经网络进行知识表示学习(附代码)
【导读】随着知识图谱越来越火,知识图谱的表示渐渐成为研究重点,目前已经有 TransE,TranH,ComplEX 等一系列的方法,这些方法在标准数据集中都取得了较好的结果,但在其他数据集上结果不是很理想。这篇文章提出一个基于简单神经网络的知识表示模型,在众多数据集中均取得了较好的结果。
论文链接:https://arxiv.org/abs/1711.05401
论文代码:
https://github.com/Srinivas-R/AKBC-2017-Paper-14
▌摘要:
我们解决了知识库补充和知识图谱中学习实体和关系向量表示问题。这个问题近几年来受到了很大的关注,并且许多方法被提出了,文献中大部分的方法是用预定义的特征评分函数来评估KG三元组的正确性。评分函数将正确的三元组(高分)与不正确的三元组(低分)区分开来分数,但是他们的表现在不同的数据集中有所不同。在我们的工作中,我们证明一个简单的基于神经网络的评分函数,这个方法能在众多数据集中取得最好的效果。我们也指出了标准数据集的缺陷,这就需要我们在不同数据集上进行实验评估。
▌介绍:
知识图谱例如NELL和Freebase是用多关系图谱来进行存储信息,被广泛应用于信息提取,问题等领域。知识图谱包含关系三元组(h,r,t)形式的世界知识,其中r用来描述h和t的关系。例如(唐纳德·特朗普,总统,美国)将表明唐纳德·特朗普是美国总统的事实。目前的知识图谱包含相当大的,数以百万计的事实,他们往往是相当稀疏。为了克服稀疏性,知识库完成或链接预测被执行来推断缺少的事实。用低维向量来表示实体和关系,也被称为嵌入,已被广泛用于这个问题。大部分采用的方法是用评分函数来区分正确三元组(高分)和错误的三元组(低分)。一些方法和其评分函数在表1总结
WN18和FB15是两个标准数据集来进行知识图谱的关系预测,先前的研究已经展示这两个数据集有着反关系偏差。这些数据集的性能在很大程度上取决于模型的预测反关系的能力,并且是以牺牲其他独立关系为代价。事实上,一个简单的基于规则的模型显示出利用这种偏见已经在这两个数据集中实现了最好的性能。为了克服这种缺点,一些数据集的变体在文献中已经被提出,例如FB15k-237,WN18RR,FB13和WN11。
ComplEx 和HolE 是目前两种流行的KG嵌入技术,它们在WN 18和FB 15k数据集有着最好的效果。然而ComplEx和HolE在其他数据集上效果并没有那么好,所以ComplEx和HolE中的预定义评分函数可能不是实现的最佳选择。所以,本文更倾向于一个在所有模型上取得接近最佳效果的模型。
在这篇文章中,作者论证了一个基于简单神经网络的评分函数,该模型能够在不同的数据集上取得近最佳的表现。这篇文章的主要贡献如下:
本文定性论证了目前的标准数据集反关系偏差问题的严重性。
本文展示了目前最好的方法没有在所有的数据集上取得同样好的效果。
本文验证了ER-MLP,一个基于简单神经网络的评分函数,能够在不同的数据集上取得近最佳的表现,也考虑了其变体ER-MLP-2d。
代码可以在这里找到:https://github.com/Srinivas-R/AKBC-2017-Paper-14
▌模型介绍:
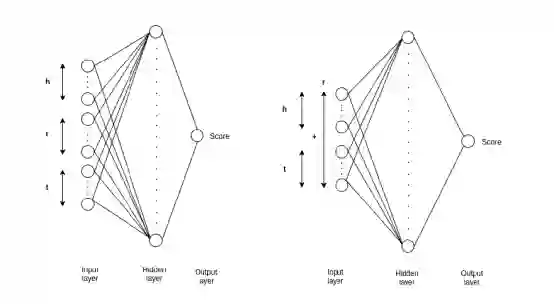
本文用一个神经网络来共同学习评分函数和三元组的向量表示,采用一个简单的只有一个隐藏层的前馈神经网络来作为给定三元组的评分函数的近似器。上图中左边为ER-MLP模型,右边为ER-MLP-2d模型,h,t为分别为h,t的d维向量表示,类似的,r也为r的向量表示,在ER-MLP为d维,ER-MLP-2d为2d维。在ER-MLP中,头,尾,关系表示连接在一起然后作为NN的输入,所以输入层的维度为3d。在ER-MLP-2d中,头,尾的表示连接在一起,然后和关系表示组合在一起,所以在EP-MLP-2d中,输入层的维度为2d。这两个模型都有一个全连接隐藏层,然后给输出节点,作为给定(h,r,t)的评分函数。
三元组的评分函数如下所示:
其中g()是激活函数,[a,b]为向量a,b的连接,M和A分别为隐藏层和输出层的权重矩阵,b是偏置。本文考虑sigmoid函数,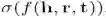
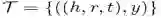
▌实验结果:
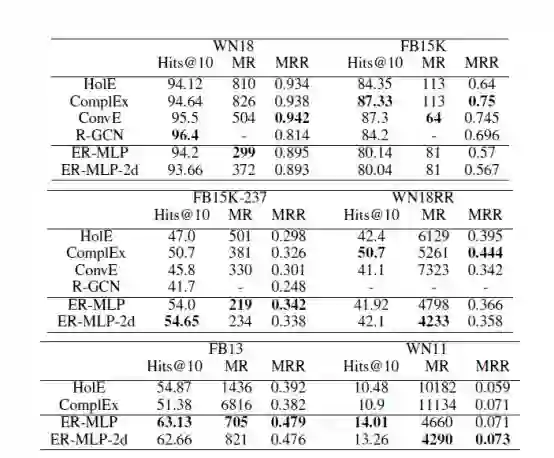
上表为关于实体预测方面不同方法在不同数据集的表现,从中可以看出基于神经网络的模型在WN11.FB13和FB15K-237有着做好的表现,并且在WN18上有着很大的竞争力,ComplEX和HolE在WN18RR比神经模型表现的更好。
▌结论
在本文中,作者提出了一个简单的基于神经网络的知识表示方法,并且在不同数据集上均取得了较好的效果,甚至在一些数据集中有目前为止最好的表现。
-END-
专 · 知
人工智能领域主题知识资料查看获取:【专知荟萃】人工智能领域26个主题知识资料全集(入门/进阶/论文/综述/视频/专家等)
同时欢迎各位用户进行专知投稿,详情请点击:
【诚邀】专知诚挚邀请各位专业者加入AI创作者计划!了解使用专知!
请PC登录www.zhuanzhi.ai或者点击阅读原文,注册登录专知,获取更多AI知识资料!
请扫一扫如下二维码关注我们的公众号,获取人工智能的专业知识!
请加专知小助手微信(Rancho_Fang),加入专知主题人工智能群交流!
点击“阅读原文”,使用专知!