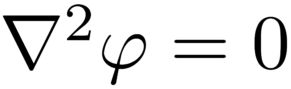拉普拉斯方程之美：万物的数学之匙

2017 年 11 月 27 日 算法与数学之美

物理是一个天生自带暗语密码的学科。而正是这些密码将宇宙里的各种秘密转为人类语言。它们可以把最纯粹的数学和任意物理下的分科联合在一起。而这，正是其中之一。

它存在于电磁学，存在于流体力学，存在于万有引力，存在于热力学，也存在于表面张力里。它，乃是拉普拉斯方程。它，无处不在。

拉普拉斯方程是由皮埃尔-西蒙·拉普拉斯（Pierre-Simon Laplace）首先提出而得名的。拉普拉斯则是一位世界著名的法国数学家，在维基百科上甚至有数个被冠以他的名字的页面。在1799年，他证明了在天文时间单位里，太阳系是一个稳定的系统，推翻了一个世纪前牛顿的假设。在这个过程中，拉普拉斯方程诞生了。

皮埃尔-西蒙·拉普拉斯

它只有5个符号。被平方的一个名为向量算子的倒三角，希腊字母φ，等号，零。通过这五个符号，拉普拉斯读懂了宇宙。

φ，这个方程的精髓，通常代表势能。虽然它也可以代表其他的数值，但是在这里，我们将φ定为代表一片陆地每一点的海拔。山坡上的φ很大，山谷里的φ则很小。

被一系列运算所代表的向量算子平方被称之为拉普拉斯算子。它所测量的是在这篇陆地上移动时φ值升降之间的平衡。

在山顶上，不论任何方向，唯一的可能就是海拔的下降，因为它已是最高点。这时的拉普拉斯算子是负数，因为下降值比上升值大。山谷底则完全相反，正数的拉普拉斯算子是因为唯一的可能就是上升。而在这两者之间则存在着一处平衡点，在那，一步可能带来的上升和下降完全相同。在这处平衡点上，拉普拉斯算子为零。

在拉普拉斯方程里，一片陆地上所有地点的拉普拉斯算子都等于零。而这有两个结果。第一，在任何一个位置上，你都可以上升或下降相同的海拔。第二，一片陆地最高和最低的φ值都只能存在于边境。这是因为，如果φ值有变，它只能在抵达峰顶或谷底之前发生。

现实的地面很难符合拉普拉斯方程，但是皂膜不一样。把一个铁圈放进肥皂水里再拿出来，你将发现制造出来的皂膜会没有任何起伏。你可以拿着铁圈换一换姿势，但是你会发现你没有任何办法使皂膜高出或底出铁圈。从任何角度来看，铁圈的边缘都是这个平面的最高与最低点。

皂膜之所以形成这个形状是由于表面张力导致的。但是拉普拉斯算子完美的预料到并描述了它。而且你要记住，拉普拉斯发明出这个方程的原因是因为它描述了整个太阳系。

让我们用另外一个例子来描述拉普拉斯方程。想象一块带电荷的金属在空无一物的太空中。通常，太空中是没有电压的。但是，此时金属附近的空间会有和金属相似的电压。距离金属更远的空间电压则会更小，但只有在离金属无穷远的时候电压才会为零。当你离开金属所在的那点，你不会测量到任何电压的波动，因为没有任何其他电荷来导致电压波动。电压只会随着距离的增加而变小。

如果你想知道空间里任何一点的电压，你只需要解开拉普拉斯方程。

听起来很难？不用担心，拉普拉斯方程厉害之处在于，如果你想解开皂膜的拉普拉斯方程，你在最后一步之前不需要任何关于铁圈的数值。所有的步骤完全独立于铁圈。所以，你可以把它完美的套用在电压的计算上。除了最后一步，这个方程不会有一丁点的改变。

同样，它可以被运用在任何地方，只要你把最后一步改好。引力在物体表面最大，但是会渐进归零，拉普拉斯方程可以计算它。水流的速度在被阻碍时为零，但是在远处则不会有任何影响，拉普拉斯同样好使。鼓面被紧固在鼓上，它的表面张力使它持平，拉普拉斯对它也有效。

横跨宇宙，横跨教室，横跨研究，只要你注意找，拉普拉斯方程必然会出现。而你，只需要解它一次。