关于神经网络，一个学术界搞错了很多年的问题

2022 年 4 月 22 日 夕小瑶的卖萌屋

文 | 五楼@知乎

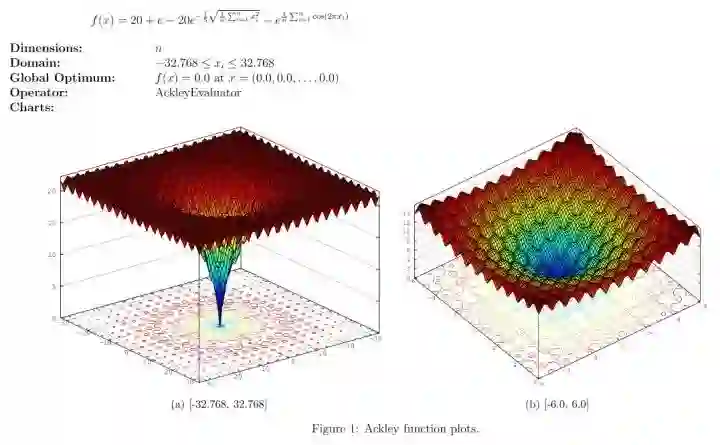
说一个近年来神经网络方面澄清的一个误解。BP算法自八十年代发明以来，一直是神经网络优化的最基本的方法。神经网络普遍都是很难优化的，尤其是当中间隐含层神经元的个数较多或者隐含层层数较多的时候。长期以来，人们普遍认为，这是因为较大的神经网络中包含很多局部极小值（local minima），使得算法容易陷入到其中某些点。这种看法持续二三十年，至少数万篇论文中持有这种说法。举个例子，如著名的Ackley函数。对于基于梯度的算法，一旦陷入到其中某一个局部极值，就很难跳出来了。(图片来自网络，压缩有点严重。原图可见Documentation/Reference/Test Functions - HeuristicLab[1]）。

到2014年，一篇论文《Identifying and attacking the saddle point problem in high-dimensional non-convex optimization》[2]，指出高维优化问题中根本没有那么多局部极值。作者依据统计物理，随机矩阵理论和神经网络理论的分析，以及一些经验分析提出高维非凸优化问题之所以困难，是因为存在大量的鞍点（梯度为零并且Hessian矩阵特征值有正有负）而不是局部极值。

鞍点（saddle point)如下图（来自wiki）。和局部极小值相同的是，在该点处的梯度都等于零，不同在于在鞍点附近Hessian矩阵有正的和负的特征值，即是不定的，而在局部极值附近的Hessian矩阵是正定的。

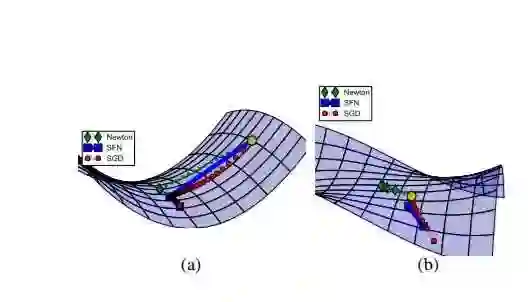
在鞍点附近，基于梯度的优化算法（几乎目前所有的实际使用的优化算法都是基于梯度的）会遇到较为严重的问题，可能会长时间卡在该点附近。在鞍点数目极大的时候，这个问题会变得非常严重（下图来自上面论文）。

这个问题目前仍有讨论，不过大体上人们接受了这种观点，即造成神经网络难以优化的一个重要（乃至主要）原因是存在大量鞍点。造成局部极值这种误解的原因在于，人们把低维的直观认识直接推到高维的情况。在一维情况下，局部极值是仅有的造成优化困难的情形（Hessian矩阵只有一个特征值）。该如何处理这种情况，目前似乎没有特别有效的方法。（欢迎评论告知）

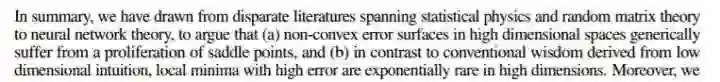
多解释一点。

鞍点也是驻点，鞍点处的梯度为零，在一定范围内沿梯度下降会沿着鞍点附近走，这个区域很平坦，梯度很小。
优化过程不是卡在鞍点不动了(像人们以为的局部极值那样)，而是在鞍点附近梯度很小，于是变动的幅度越来越小，loss看起来就像是卡住了。但是和local minima的差别在于，如果运行时间足够长，SGD一类的算法是可以走出鞍点附近的区域的（看下面的两个链接）。由于这需要很长时间，在loss上看来就像是卡在local minima了。然而，从一个鞍点附近走出来，很可能会很快就进入另一个鞍点附近了。
直观来看增加一些扰动，从下降的路径上跳出去就能绕过鞍点。但在高维的情形，这个鞍点附近的平坦区域范围可能非常大。此外，即便从一个鞍点跳过，这个跳出来的部分很可能很快进入另一个鞍点的平坦区域—— 鞍点的数量(可能)是指数级的。

各种优化算法在鞍点附近形态的展示，可以看动态图[An overview of gradient descent optimization algorithms][3]最下面的部分，非常生动形象。中文可见[SGD，Adagrad，Adadelta，Adam等优化方法总结和比较][4]。

有人提到了遗传算法和进化算法（EA），这里统一说一下。

先说优点，EA通常是不依赖于函数值的，而只依赖于点之间的大小关系，comparison-based，这样进行迭代的时候不会受到梯度太小的影响。看起来似乎是一个可行的路子？下面说一下缺点。

说说进化算法面对的一些普遍问题。

先说CMA-ES，这是效果最好最成功的进化算法之一，尤其是在ill-conditioned 问题和non-separable 问题上。CMA-ES （Covariance Matrix Adaptation-Evolution Strategy）和EDA (Estimation of Distribution Algorithm)的特点是 model-based，他们从一个正态分布采样产生一组新解，使用较好的一部分（一半）新解更新分布的参数（mean， cov或对应的Cholesky factor，对CMA-ES来说还有一个独立步长）。CMA-ES和EDA这样基于分布的算法大体上都能从information geometric optimization （IGO）用natural gradient 得到。IGO流的收敛性和算法本身在一类问题上的收敛性都不是问题，Evolution path更是动量的类似。然而这些方法最大的问题在于，由于依赖随机采样，当维度很高的时候采样的空间极大，需要极多的样本来逐渐估计cov ( )量级），采样产生新解的时候的复杂度是(不低于） )。EA的论文普遍只测试30,50-100维，500-1000维以上的极少，即便是各种large scale的变种也大多止步于1000。对于动辄量级的神经网络优化，基本是不可行的。
DE/PSO这类算法。特点是无模型，不实用概率分布采样的方法产生新解，使用多个点（称为一个种群，population)之间的相互（大小）关系来模拟一个下降方向。这种基于种群的方法对有较多局部极值的问题效果较好，但是对ill-conditioned 问题性能较差，在non-separable+ill-conditioned问题效果有限。更进一步的，这类算法为了维持种群多样性，通常只进行两两比较（两两比较的选择压力小于截断选择，即某些新解不比父本好，但是比种群中其他解好，这样的解被丢弃了），好的个体进入下一代。然而随着维度增加，新生个体比父代好的比例急剧下降，在ellipsoid函数上100维左右的时候就已经降低到5%以下。实验研究[Differential Evolution algorithms applied to Neural Network training suffer from stagnation][5]

总体上，EA在连续优化问题上的主要问题就是搜索效率不高，相比基于梯度的算法要多倍的搜索。与此相似的实际上是坐标下降法（coordinate descent），同样不使用梯度，同样要求多倍的搜索。

后台回复关键词【入群】

加入卖萌屋NLP、CV与搜推广与求职讨论群

后台回复关键词【顶会】

获取ACL、CIKM等各大顶会论文集！

[1]http://dev.heuristiclab.com/trac.fcgi/wiki/Documentation/Reference/Test%20Functions

[2]https://arxiv.org/pdf/1406.2572v1.pdf

[3] http://sebastianruder.com/optimizing-gradient-descent/

[4]http://ycszen.github.io/2016/08/24/SGD%EF%BC%8CAdagrad%EF%BC%8CAdadelta%EF%BC%8CAdam%E7%AD%89%E4%BC%98%E5%8C%96%E6%96%B9%E6%B3%95%E6%80%BB%E7%BB%93%E5%92%8C%E6%AF%94%E8%BE%83/

[5]http://www.sciencedirect.com/science/article/pii/S156849461400146X