P/NP究竟是什么？复杂问题的一则简短指南

来源：Quanta Magazine

编译：Bot

编者按：说起复杂度，相信不少人会想到Jeff Dean面试Google时的一个笑话，面试官问：如果P=NP成立，你能推导出哪些结论？年轻的Dean面不改色：P=0或N=1。虽然这个经典段子令人回味无穷，但你真的理解什么是P，什么是NP吗？

对于计算机来说，做什么事是容易的，做什么事是几乎不可能完成的，这些问题构成了计算复杂度的核心。

如果计算机科学家希望能用一个叫做“复杂度”的东西对问题进行分类，那么一个问题有多困难？这会是他们需要面对的基本任务。所谓“复杂度”，它可以被看作是包含所有计算问题的一系列组，组间划分依据是解决具体问题所耗费的资源是否在某个固定数量以下，这里的资源可以是时间，也可以是内存。

以一个玩具问题为例：123,456,789,001是不是质数？对于这个问题，计算机科学家可以用现有算法快速得到答案——123,456,789,001不是质数。无论这个数字是否会变得越来越大，算法计算所需资源会一直在可控范围内，不会突破天际。

那么，新的问题产生了：它的质因子有哪些，除了1和本身，它还能被哪些数整除？通常情况下，我们认为它和上个问题拥有不同的“复杂度”。验证一个数是不是质数很简单，但找出它的所有质因子就很困难。目前，算法还不能在短时间内解决这个问题，除非我们已经有了成熟的量子计算机。

“复杂度”本身存在大量不同的类别，但在大多数情况下，我们还无法证明这一类“复杂度”和那一类“复杂度”有哪些显著不同。这些差异可能是微妙的，也可能是明显的。因此对于大多数人来说，明确分类各种复杂度也是一个艰巨的挑战。

什么是P？

代表：多项式时间复杂性类（Polynomial time）

简介：所有P问题都能被经典计算机（非量子计算机）轻松解决。

详细说明：如果一个问题是P问题，那么它必须满足在多项式时间n^c内验证一个算法问题的实例是否有解 ，其中n是输入长度，c是个常数。

典型问题：

• 这个数是否是个质数？

• 两点之间的最短路径是什么？

研究热点：P=NP是否成立？如果成立，它将颠覆计算机科学，并使大多密码学内容在一夜之间失效（当然大多数人还是认为P!=NP）。

什么是NP？

代表：非定常多项式时间复杂性类（Nondeterministic Polynomial time）

简介：如果给出了一个解，所有NP问题都能被经典计算机快速验证。

详细说明：如果一个问题有一个解，且能在多项式时间内证明这是个正解，那么这就是个NP问题。例如，假设问题的输入是字符串X，我们的目标是验证问题的解为“是”，那么我们就需要一个证明——字符串Y，用它在多项式时间内验证答案确实是“是”。

典型问题：

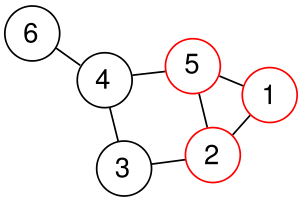
• 分团问题。想象一个带边和点的图形，我们把它当成Facebook的社交网络，一个节点代表一个用户，如果两个用户是朋友关系，那么两个节点通过边连接。一个clique表示整个社交网络中的一个子集，其中所有人都是彼此的朋友。那么也许有人会问：这个社交网络中是否存在20人的clique？50人？100人？找到这样一个clique就是个“NP-完全问题”（NPC），这意味着它具有NP中任何问题的最高复杂度。但是，如果问题是50个节点可不可以形成一个小子集，它给出了潜在答案，那么这个NP问题就很容易被验证。

红色：一个大小为3的clique

• 旅行商问题。有许多城市，每个城市之间都有对应的路程距离，旅行商能不能在不到具体里程数的情况下经过所有城市。

研究热点：P=NP是否成立？

什么是PH？

代表：多项式层级结构复杂性类（Polynomial Hierarchy）

简介：PH是NP的概括——它包含由NP问题发展而来的所有问题，并添加了额外的复杂度。

详细说明：PH问题包含一些交替“量词”的问题，使问题更加复杂。至于什么是交替“量词”，这里有一个示例：给定X，确定是否存在Y，使得对于每个Z，都存在一个W能使R成立？问题中包含的“量词”越多，它就越复杂，在多项式层级结构中也越高。

典型问题：

• 确定是否存在大小为50的clique，同时没有大小为51的clique。

研究热点：计算机科学家无法证明PH与P不同，这个问题其实相当于P与NP问题，因为如果我们（意外地）证明P=NP，那么所有的PH问题都会坍缩到P，即P=PH。

什么是PSPACE？

代表：多项式空间复杂性类（Polynomial Space）

简介：PSPACE包含在限定内存下能解决的所有问题。

详细说明：在PSPACE问题中，你不需要关心用时，只要关注运行算法所需的内存。计算机科学家已证明PSPACE问题包含PH，也就是包含NP，包含P。

典型问题：

• P、NP和PH中的每个问题都是PSPACE问题。

研究热点：PSPACE与P有何不同？

什么是BQP？

代表：有限错误量子多项式时间复杂性类（Bounded-error Quantum Polynomial time）

简介：所有BQP问题都能被量子计算机轻松解决。

详细说明：量子计算机可以在多项式时间内解决的所有问题。

典型问题：

• 确定整数的质因子。

研究热点：研究人员已经证实P⊆BQP⊆PSPACE，但他们还不能确定BQP和NP的关系，目前他们的看法是两者互斥。

什么是EXPTIME？

代表：指数时间复杂性类（Exponential Time）

简介：经典计算机可以在指数时间内解决的所有问题。

详细说明：EXPTIME问题包含之前所有的复杂性类——P、NP、PH、PSPACE、BQP和QMA等。目前研究人员已经证明EXPTIME和P不同——他们在其中发现了不属于P的问题。

典型问题：

• 国际象棋、跳棋等棋类游戏都属于EXPTIME问题。例如，如果棋盘可以是任意大小，那么在给定棋局形势下，确定哪位棋手是优势方就是个EXPTIME问题。

研究热点：现如今，研究人员已经能证明EXPTIME问题和P问题不完全一致，但他们希望能证明EXPTIME不属于PSPACE，因为前者关注时间，后者关注内存。

什么是BPP？

代表：有限错误概率多项式时间复杂性类（Bounded-error Probabilistic Polynomial time）

简介：可以通过包含随机元素的算法快速解决的问题。

详细说明：BPP问题的其他条件和P问题一致，不同的是，它允许算法中包含随机元素，包括决策随机化，它的解是个归一化的小数，只要接近1即可。

典型问题：

• 多项式恒等检验问题。给定两个公式，每个公式都生成一个包含许多变量的多项式，那么这两个公式计算的是相同的多项式吗？这是个BPP问题。

研究热点：计算机科学家想知道BPP是否是P。如果是，那这就意味着每个随机算法都可以去随机化。

原文地址：www.quantamagazine.org/a-short-guide-to-hard-problems-20180716/