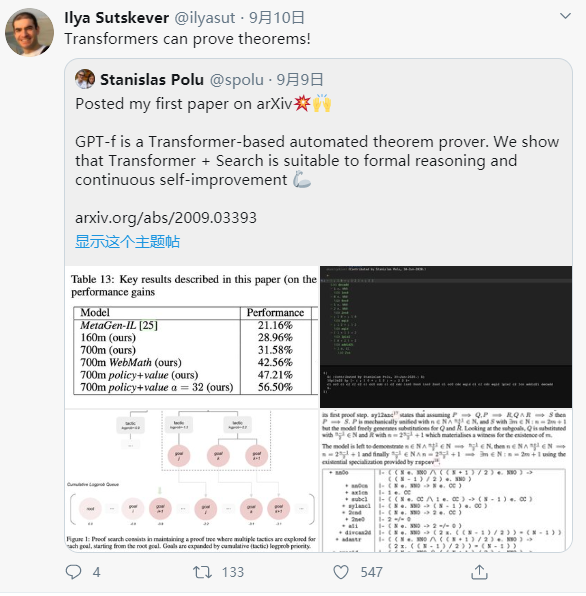
OpenAI 发布模型实现自动定理证明，妈妈再也不用担心我的数学？

作者 | 八宝粥

出品 | CSDN(ID:CSDNnews)

OpenAI 大招频出，染指数学江湖

日前，OpenAI 研究者Stanislas Polu和Ilya Sutskever在社交媒体发布消息，宣布在预印本发布文章，展示了一个基于Transformer 的自动定理证明模型。文章表示，团队在 Metamath 库上取得了新的进展，通过将深度学习和形式系统相结合能带来更好的效果。

论文两位作者在社交网络分享发布新模型的喜悦

团队表示，GPT-f 可以自动证明 Metamath 当中23个定理。横向对比上，GPT-f 最佳模型实现 Metamath 56.22% 的保留测试集，而目前最先进的 MetaGen-IL 只有 21.16% 的证明能力。

文章还给出了数据集 set.mm 和证明助手的一个 demo：

“自动定理证明”对于饱受数学困扰的同学来说简直就是大杀器，比拟“步步高点读机”，笔者不禁想到自己中学数学做题时自信地刷刷写下“证明”二字和面对高等数学挠头时候的“这也能证？”，“要是机器能帮我证明就好了”。

实际上，在数学界，确实有很多问题需要机器来帮忙。但是 GPT-f 真的是数学界的 AlphaGo 吗？数学家也要望机器兴叹了吗？似乎也并不是这样。

数学天才也需要机器

前段时间获得诺贝尔物理学奖的科学 家罗杰·彭罗斯 ，他在数学方面有一个很有趣的贡献，就是彭罗斯密铺，1976年，他提出采用两种不同的菱形进行密铺，实现对平面的全覆盖。而放眼三维，早在十七世纪，德国天文学家开普勒就对三维欧式空间当中容纳球的方式进行研究，发现三维球堆积的最大密度为：

而这个定理直到 1998 年由机器来辅助证明的。就是那种你明明知道却证不出来的感觉。直到 2014年才由黑尔斯的 FlysPeck 项目完成了形式化证明。

说到推理，就肯定会提到计算机界的鼻祖图灵大佬。二战期间，德军采用恩格玛机器加密，给盟军的情报获取造成了极大的打击。为了破解密码，盟军招募大量人力组建团队，对密码机进行研究，后发明“图灵炸弹（Turing Bombe）”，虽然对恩格玛的破解是波兰人，但是毫无疑问图灵是恩格玛破解的最大功臣。此后“图灵炸弹”在布莱切利继续发挥作用，给密码破译工作加速。图灵以他的名字命名的抽象计算模型——图灵机也是通过机器来模拟人类计算的过程。后来成为计算机历史上具有浓墨重彩的一页。

机器辅助证明已经成为了单独的数学研究方向，而人工智能更多地研究的是让机器自主去发现和探索数学定理。就好比 AlphaG o 或者 AutoML 一样，机器可以自己去探索和研究。 人们期待计算机能给人带来更多惊喜。 GPT 这种惊人能力让人想到了当年的印度天才拉马努金，他从来没有经历专业的数学训练。 凭借自己的天赋，用自己的符号和方式证明了很多已经存在的定理。 著名的数学家哈代发现了他的天赋，将其带往英国，后发现了拉马努金猜想、整数分割和θ函数等著名的数学定理。 如果机器真的都能变成一个个拉马努金，那么不久的将来在数学甚至信息学界就会发生翻天覆地的变化。

保持慎重,保持乐观

对于 GPT 模型，很多人并不乐观，像此前一直对 GPT 开炮的 Gary Marcus, 在社交媒体上一直置顶自己在《MIT 科技评论》上面批判 GPT 的文章，文中批评了 GPT 在面对数学等基础学科上的无知和无能，称其根本一文不值，只是一个了解上下文的机器而已。此次更是快速反应, 称 GPT-f 也一样达不到人类的水平，更不用说打败人类了。

Robust.AI联合创始人一直都不喜欢GPT，此次依然直接吐槽

这里我们也表示乐观，如果 GPT-f 真的能够实现更大的突破，那么不管是数学界还是在 AI 界，都是拉马努金在世一样的好事，毕竟这位印度天才如果不是在异国他乡身体虚弱，说不定还能创造更多的数学奇迹。如果 GPT-f 不能跟真人一样, 说不定还会有 GPT-G, GPT-X, GPT-Y 呢～

注: Metamath是用来发展严格形式化数学定义及证明的一款语言，亦指用来验证该语言的证明验证器，以及存有逻辑、集合论、数论、群论、代数、数学分析、拓扑学、希尔伯特空间及量子逻辑等领域中数万条已证明定理且仍不断在增加中的数据库。(来源: 维基百科)
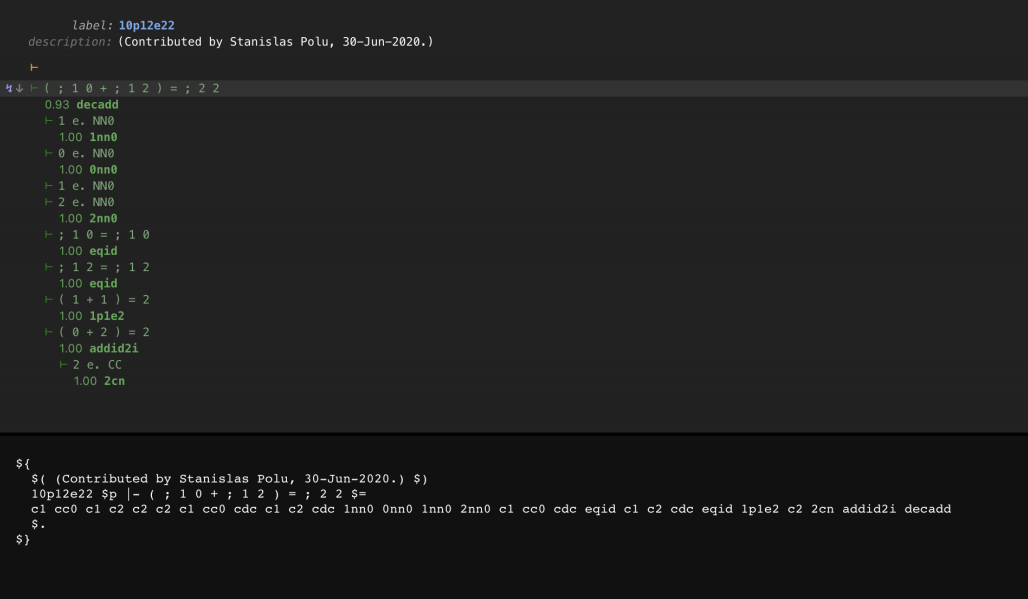
论文链接:https://arxiv.org/abs/2009.03393

更多精彩推荐

☞去伪存真，更多区块链落地应用即将涌现
☞你认为程序员的最高境界是什么？| 每日趣闻
☞虎牙、斗鱼正式达成合并协议；中国广电正式成立，或催生5G发展新格局；Linux 5.9 释出|极客头条
☞8000字 | 32 张图 | 一文搞懂事务+隔离级别+阻塞+死锁
☞图神经网络快速爆发，最新进展都在这里了
☞今年至少有75家交易所关闭，近半数没有说明原因

点分享
点点赞
点在看