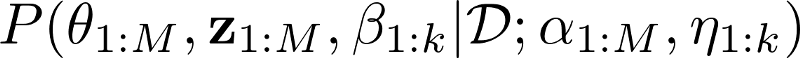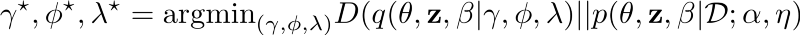机器学习当中的数学闪光：如何直观地理解 LDA

2018 年 10 月 11 日 AI研习社

本文为 AI 研习社编译的技术博客，原标题：

Light on Math Machine Learning: Intuitive Guide to Latent Dirichlet Allocation

翻译 | W@SYSU、乔叔叔、cold、懒虫半成品

校对 | 老赵整理 | 志豪

原文链接：

https://towardsdatascience.com/light-on-math-machine-learning-intuitive-guide-to-latent-dirichlet-allocation-437c81220158

主题建模是指识别用于描述一组文档的最合适的主题。这些主题只有在主题建模过程中才会出现（因而称为隐藏的）。一个流行的主题建模方法就是广为人知的Latent Dirichlet Allocation(LDA)。尽管这个名字有点拗口，但其背后的想法却是相当简单。

简单地讲，LDA虚构一组固定主题，每个主题表示一组词汇。LDA的目标是使用一种方法将所有文档映射到主题上，使得这些虚构的主题概括了文档中的大部分词汇。我们会系统地介绍这个方法直到最后你能自如地运用。

这是机器学习中的数学闪光系列A-Z的第四个博客，你可以在以下的字母中找到以往博客的链接。

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

为什么需要主题建模?

主题建模在现实世界中有哪些应用？通过分析基于年份的文本，历史学家可以使用LDA辨别重要的历史事件。在线图书馆根据你以往的阅读记录，能够使用LDA向你推荐书籍。新闻出版商可以应用主题建模快速理解文章或将相似的文章聚类到一起。另一个有趣的应用是无监督图像聚类，其将每张图像类似文档看待。

这篇文章有什么独特之处？不就是另一个豆腐块而已吗？

简短的回答是一个大写的“NO”。我浏览过许多不同的文章，有许多不错的文章和视频给出关于LDA的直观印象，然而它们大部分没有回答像如下的一些问题：

1. LDA背后的直觉理解是什么？

2. 什么是狄利克雷分布？

这些在本文都会谈及，但我相信不应止于此。我读的大部分文章没有说明关键部分-模型训练的方法。因而，我尝试回答更多的一些问题，如

1. 我们感兴趣求解的数学实体是什么？

2. 我们如何求解这些数学实体？

LDA的大思路是什么？

一旦理解LDA的大思路，我认为这会帮助你理解LDA的原理为什么是这样子的。这个大思路即是

每个文档可以被描述为一个关于主题的分布，每个主题可以被描述为一个关于词汇的分布。

为什么是这个思路？我们可以通过一个例子来反映。

用门外汉的话解读LDA

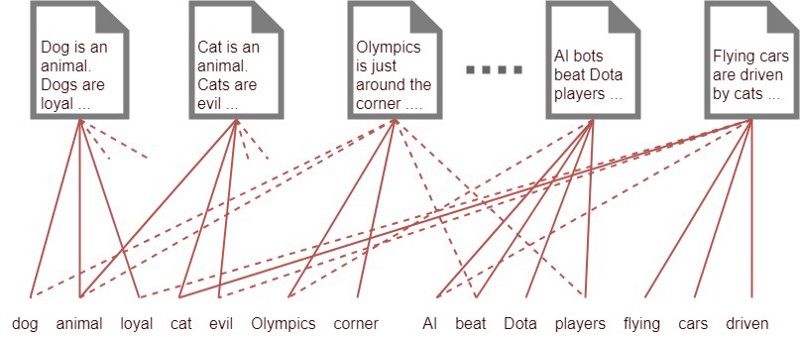
比如你有1000个单词的集合(即所有文档中最常见的1000个单词)和1000份文档。假设每份文档平均有500个单词出现在这些文档中。你怎么知道每篇文档属于哪个类别？一种方法是将每篇文档使用一根线连接到每个出现在文档中的单词，如下图所示：

仅仅使用词汇对文档进行建模。你可以看到，由于存在大量的连线，我们并不能从中推断出有用的信息。

你会看到，一些文档连接到相同的词汇集上，它们是在讨论同一个话题，阅读其中一篇文献便能知道其他文献讨论的内容。然而，为达到这样的目的，你并没有足够的线，这大概需要500*1000=500,000根线。想象一下我们生活在2100年，并且穷尽了所有资源来生产这些线，它们非常昂贵以致于你只能负担起10,000根线。你怎么解决这个问题呢？

更深入一步减少线的数量

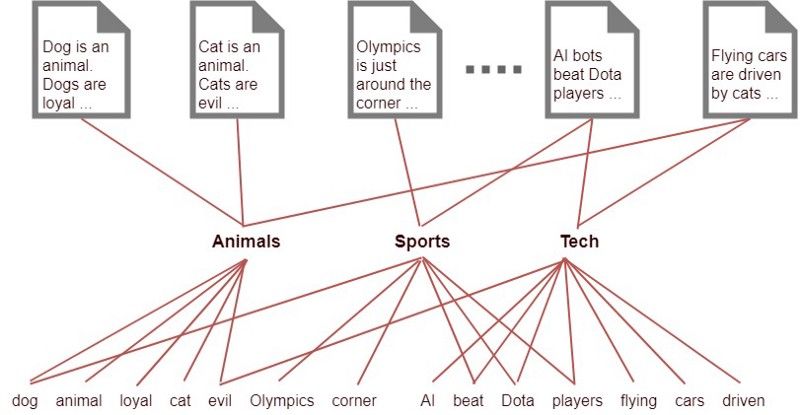
我们可以通过引入一个隐藏层来解决这个问题。假如我们知道有10个主题可以描述所有的这些文档，但我们并不知道这些主题是什么，只知道词汇和文档，因而这些主题是隐藏的。我们希望使用这些信息来减少线的数量。你可以做的是，根据单词与主题的贴合程度，将主题与单词连接起来，然后根据每篇文档涉及的主题将文档与主题连接起来。

现在假设每篇文档大概有5个主题，每个主题涉及500个单词。这里我们需要1000*5根线将文档和主题连接起来，还有10*500根线连接主题和单词，共10000根线。

文档和单词均使用一组主题来建模。这种关系比第一个例子更为清晰，因为这里使用了更少的线。

注意：我这里使用的主题（“Animals”, "Sports"，"Tech"）是虚构的，真正的求解结果如使用（0.3*Cats, 0.4*Dogs, 9，0.2*Loyal，0.1*Evil）表示“Animals”这个主题，即如前所述，每篇文档为单词的分布。

一个不同的观点:LDA假设文档如何生成?

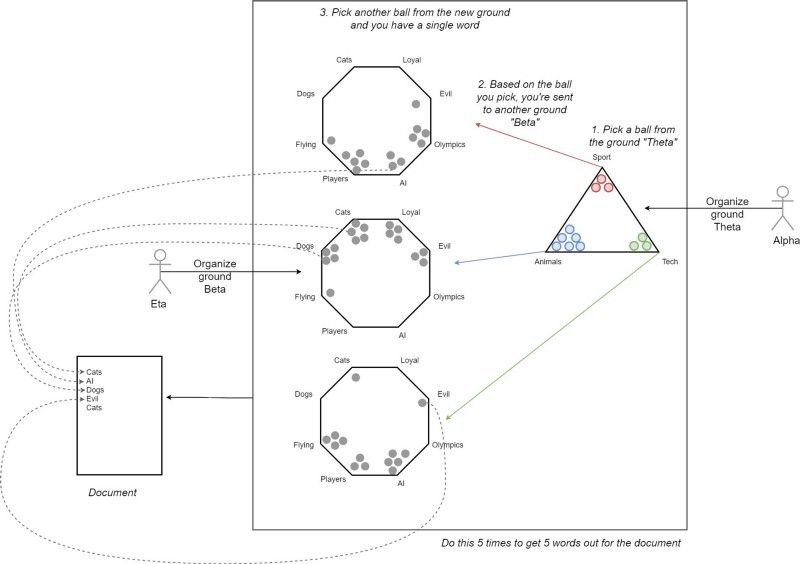
为了提供更多的背景信息,LDA假设任何你看到的文档背后都有以下生成过程.简单起见,我们假设我们生成一个包含五个词的文档.但是同样的生成过程适用于包含N个词的M个文档中的每个文档.图注里已经说得很详细了，大家看图就好，我就不再啰嗦一遍了。
文档是如何生成的.首先,α(alpha)组织了地面θ(theta),然后你从中挑出一个球.根据你的选择,你被送到了地面β(beta),β由η(Eta)组织.现在你从β中选择一个词,并将其放入文档.你迭代这个过程5次,得到5个词.
这幅图表现了经过学习了的LDA系统的样子.但是要达到这个阶段,你需要回答几个问题,比如:

我们如何知道文档中有多少个主题?

你了解了我们已经在地面上有一个可以帮助我们生成合理文档的很好的结构,因为组织者确保了正确的地面设计.我们如何找到这样的好的组织者?

这将在接下来的几节中回答.此外,从这里开始我们将会有点技术性.因此注意这里会有些难度啦!
注意 :LDA不关心文档中单词的顺序.通常来说,LDA使用词袋特征表示来表示文档.这是有道理的,因为如果我拿一个文档,打乱词汇并将它交给你,你仍然可以猜出文中讨论了哪些主题.

获得一些数学知识...

在深入学习细节之前,让我们看看一些符号和定义之类的东西.

定义和符号
k——文档所属的主题数(一个固定值)
V——词典大小
M——文档数量
N——每个文档中的词数
w——文档中的词.表示为一个长度为V(即词典大小)的独热编码的向量
w(粗体w):便是为一个N个词的文档(即w的向量)
D——语料库,M个文档的集合
z——来自一组k个主题中的一个主题.主题是词的分布表示,例如它可能是,动物=(0.3猫,0.4狗,0AI,0.2忠诚,0.1邪恶)

以更偏数学的方式定义文档的生成

首先让我们将基于地面的例子放在上面生成文档,加以合适的数学描绘.

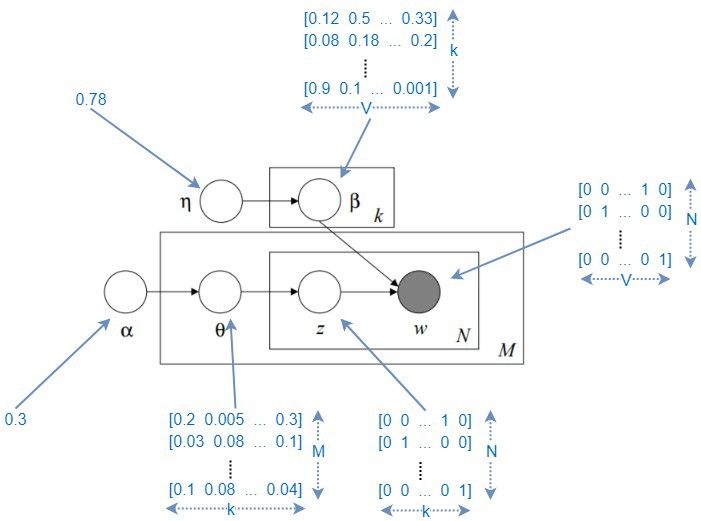
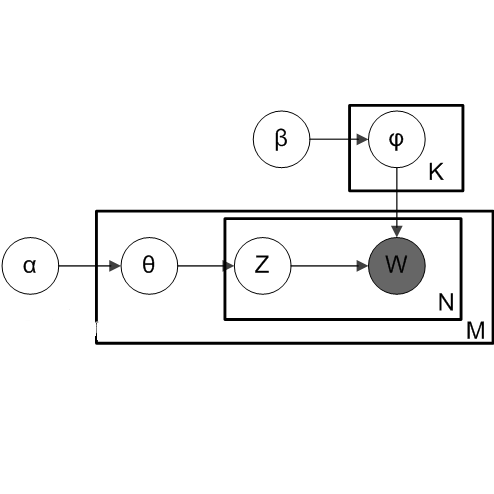
LDA的图形模型.这里我标记了所有可能的变量的维度(同时有观察变量和隐变量).但是请记住θ,z和β是分布,不是确定值.

让我们解读下它的含义.我们有一个值α(即地面θ的组织者),它定义了θ;这类似于文档的主题分布.我们有M个文档,对每个文档都有一些θ分布.现在为了更清楚地理解它,眯起你的眼睛,让M消失(假设仅有一个文档)。

现在这个文档有N个词,每个词都是由一个主题生成的.你生成了N个主题以填充这些词.这N个词仍然是占位符。

现在重点来了.基于η,β具有一定的分布(准确的说是狄利克雷分布-很快会讨论到),同时根据该分布,β为每个主题生成了k个独立的词。现在,你为每个占位符填写一个词(在N个占位符集合中),以它所代表的主题为条件。

你得到一个由N个词组成的文档了!

为什么 α和η被显示为常量

在上图中，α和η被显示为常量，但是实际上却复杂得多。例如，针对每一篇文档，α都有一个主题分布(就是例图中的场地θ)。理想状态下，是个(M x K)形状的矩阵。针对每一个主题，η都有一个参数向量，η的形状将是(k x V)。在上图中，这些常量实际上是矩阵，通过向每个单元复制一个单一值，从而形成了这些常量。

让我们更详细地理解 θ 和 β

θ是一个随机矩阵，其中θ(i,j)代表的是第i篇文档包含属于第j个主题的词的概率。如果你再回看一下上面图例中场地θ的样子，你就能够看出这些球都被整齐地排在了三角形场地的角落里，而不是在中间。这样的优势是，我们生成的词非常可能属于某个单一主题，就像真实世界里的文档一样。而正是因为让θ按照狄利克雷分布，才使我们拥有该特性。相似的，β(i,j)代表的是第i个主题包含第j个词汇的可能性。而且β也是一个狄利克雷分布。下面，为了理解狄利克雷分布，我会加入一个小插曲。

小插曲：理解狄利克雷分布

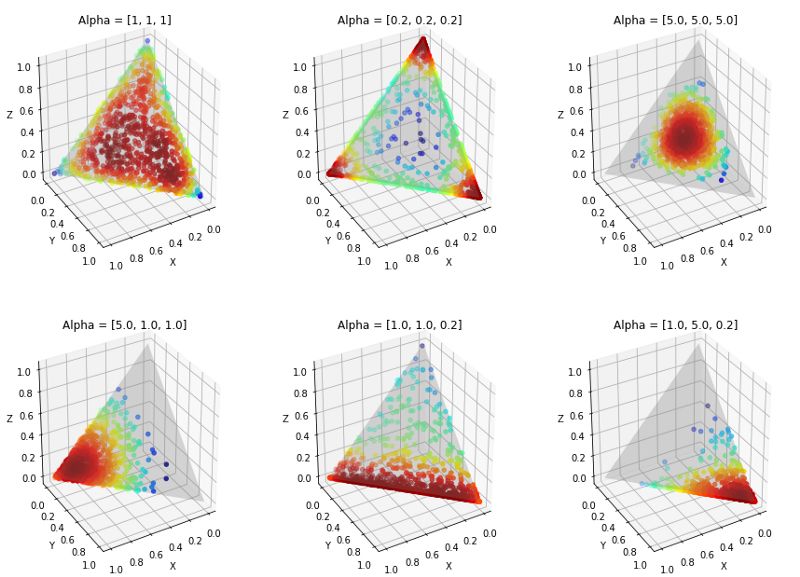
狄利克雷分布是Beta分布的多元泛化形式。在这里我们讨论一个3维的例子，在α中，我们有3个参数，它们能影响到θ的形状（即分布）。对于一个N维的狄利克雷分布而言，你会有一个长度为N的向量α。你会看到对于不同的α取值，它是如何改变θ的形状的。例如，你可以看到顶部中间的图表显示出了和场地θ相似的形状。

你需要记住的要点如下：大的 α取值会将空间分布向三角形的中间挤压，而较小的α取值则将空间分布推向三角形的角落。