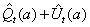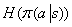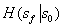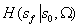强化学习的两大话题之一,仍有极大探索空间

编译 | bluemin
-
-贪婪:智能体以较小的概率
进行随机探索,在大多数情况以概率
选择当前的最优动作。
-
置信区间上界(UCB):智能体选择当前最优的动作来最大化置信区间上界 ,其中
是到时间 t 为止与动作 a 有关的平均奖励函数,
是与已执行动作 a 的次数成反比的函数。
-
玻尔兹曼探索策略:智能体根据学习到的由温度参数 调节的Q值,从玻尔兹曼分布(softmax函数)中选择动作。
-
汤普森采样:智能体将追踪记录的最优动作概率作为先验分布,然后从这些分布中采样。
-
熵损失正则项:在损失函数中加入熵正则项 ,鼓励智能体选择包含多元化动作的策略。
-
基于噪声的探索:在观察、动作甚至在参数空间中添加噪声。
2
探索问题之关键
1、硬探索问题
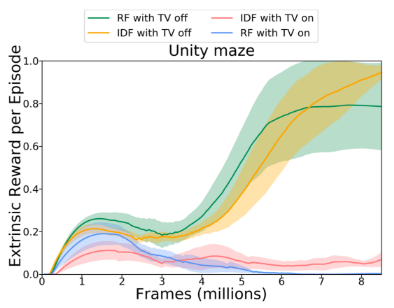
2、电视加噪问题

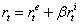 ,其中
,其中
-
根据当前任务所定义, 是在 t 时刻来自环境的外部奖励。
-
是当前时刻 t 的内在探索奖励。
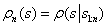 ,表示在前 n 个状态是
,表示在前 n 个状态是
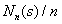 。
。
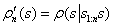 定义:当观察到s的新状态出现,密度模型分配给状态 s 的概率。
定义:当观察到s的新状态出现,密度模型分配给状态 s 的概率。
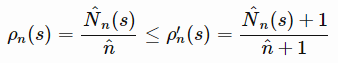
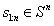 和
和
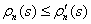 。换言之,在观察到 s 的一个实例后,密度模型对该 s 的预测概率也要相应地增加。除了需要正向学习外,密度模型还要利用非随机化的经验状态数据,进行在线训练,由此可以得到
。换言之,在观察到 s 的一个实例后,密度模型对该 s 的预测概率也要相应地增加。除了需要正向学习外,密度模型还要利用非随机化的经验状态数据,进行在线训练,由此可以得到
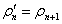 。
。
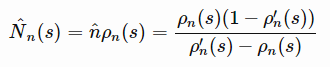
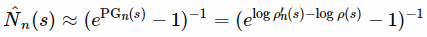
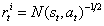 (如MBIE-EB;2008年论文《An analysis of model-based Interval Estimation for Markov DecisionProcesses》)。基于伪计数的探索附加奖励的形式类似于
(如MBIE-EB;2008年论文《An analysis of model-based Interval Estimation for Markov DecisionProcesses》)。基于伪计数的探索附加奖励的形式类似于
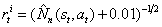 。
。
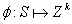 离散化。将探索附加奖励
离散化。将探索附加奖励
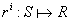 添加到奖励函数中,定义为
添加到奖励函数中,定义为
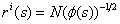 ,其中 N(ϕ(s)) 是 ϕ(s) 出现的经验计数。
,其中 N(ϕ(s)) 是 ϕ(s) 出现的经验计数。
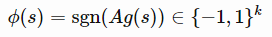
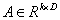 是一个矩阵,每一项都相互独立,并服从标准高斯分布,
是一个矩阵,每一项都相互独立,并服从标准高斯分布,
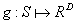 是可选的预处理函数。二进制码的维度为k,控制状态空间离散化的粒度。k 越高,粒度越大,碰撞越少。
是可选的预处理函数。二进制码的维度为k,控制状态空间离散化的粒度。k 越高,粒度越大,碰撞越少。

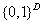 ,再将此二进制数作为状态 s 的二进制哈希码。n 个状态的 AE 损失包括重构损失和 sigmoid 激活函数的二进制近似损失两项:
,再将此二进制数作为状态 s 的二进制哈希码。n 个状态的 AE 损失包括重构损失和 sigmoid 激活函数的二进制近似损失两项:
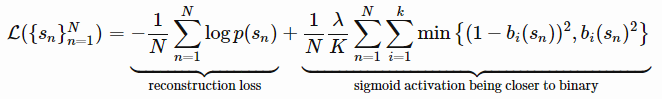
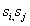 可能会映射成相同的哈希码,但是自动编码器仍然会很好的重构它们。我们可以用哈希码 ⌊b(s)⌉ 替换瓶颈层 b(s),但是这样做,梯度不能通过round函数进行反向传播。 注入均匀噪声可以减轻这种影响,促使自动编码器学会扩大隐变量间的距离以抵消噪声。
可能会映射成相同的哈希码,但是自动编码器仍然会很好的重构它们。我们可以用哈希码 ⌊b(s)⌉ 替换瓶颈层 b(s),但是这样做,梯度不能通过round函数进行反向传播。 注入均匀噪声可以减轻这种影响,促使自动编码器学会扩大隐变量间的距离以抵消噪声。
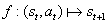 。在部分可观测的问题中,这种模型是不完备模型,其中误差
。在部分可观测的问题中,这种模型是不完备模型,其中误差
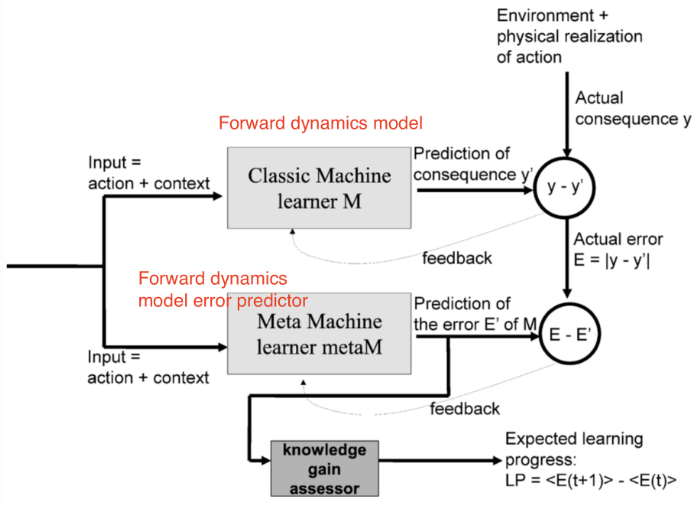
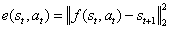 可作为内在探索奖励的标准。预测误差越大,说明我们对这种状态就越不熟悉。错误率下降得越快,我们获得的学习信号将越多。
可作为内在探索奖励的标准。预测误差越大,说明我们对这种状态就越不熟悉。错误率下降得越快,我们获得的学习信号将越多。
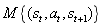 和前向动态模型 f。IAC 基于转换样本将状态空间(如论文中所讨论的机器人上下文运动空间)渐进地分割成不同的区域,此过程类似于不断分枝的决策树:当样本数大于一个阈值时产生分枝,并且每个叶子的状态变化应该是最小的。每一个树节点都有其唯一的样本集和称之为“专家”的前向动态预测因子 f。
和前向动态模型 f。IAC 基于转换样本将状态空间(如论文中所讨论的机器人上下文运动空间)渐进地分割成不同的区域,此过程类似于不断分枝的决策树:当样本数大于一个阈值时产生分枝,并且每个叶子的状态变化应该是最小的。每一个树节点都有其唯一的样本集和称之为“专家”的前向动态预测因子 f。
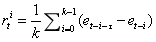 ,其中 k 是滑动窗口的大小。因此,预测错误率降低幅度越大,分配给智能体的内在奖励就越高,即鼓励智能体迅速采取动作来了解当前的环境。
,其中 k 是滑动窗口的大小。因此,预测错误率降低幅度越大,分配给智能体的内在奖励就越高,即鼓励智能体迅速采取动作来了解当前的环境。
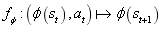 。模型在 T 时刻的预测误差用 T 时刻的最大误差进行归一化,
。模型在 T 时刻的预测误差用 T 时刻的最大误差进行归一化,
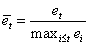 ,因此它总是在0到1之间,根据此可以定义内在奖励为:
,因此它总是在0到1之间,根据此可以定义内在奖励为:
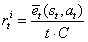 ,其中 C>0 是衰减常数。
,其中 C>0 是衰减常数。
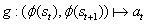 ,特征空间只捕捉与智能体动作相关的环境变化,而忽略其余的变化。
,特征空间只捕捉与智能体动作相关的环境变化,而忽略其余的变化。
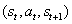 :
:
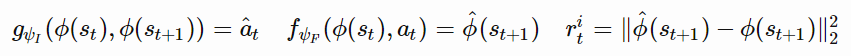
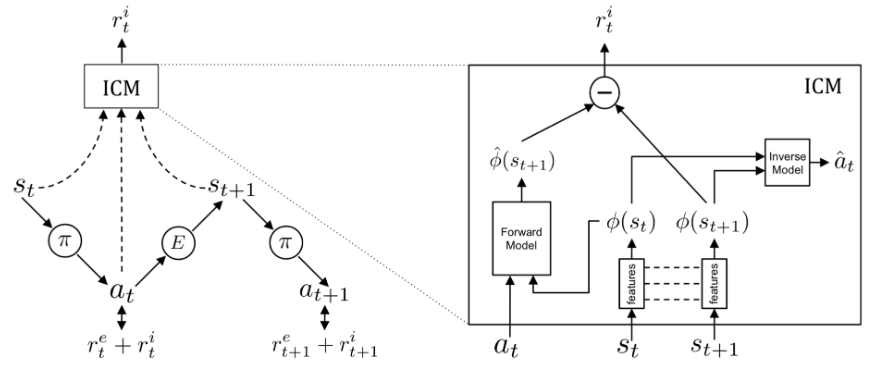
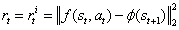 。ϕ 值选取合理将使学习过程紧凑、充分、稳定,易于处理预测任务,并能滤除不相关的观测值。
。ϕ 值选取合理将使学习过程紧凑、充分、稳定,易于处理预测任务,并能滤除不相关的观测值。
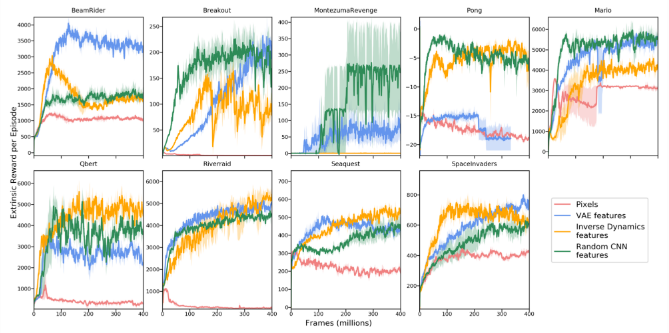
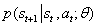 表示前向预测模型,利用
表示前向预测模型,利用
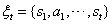 记录了轨迹历史信息。我们希望智能体在采取新的动作和观察下一个状态后降低熵值,这是为了最大化下面的表达式:
记录了轨迹历史信息。我们希望智能体在采取新的动作和观察下一个状态后降低熵值,这是为了最大化下面的表达式:
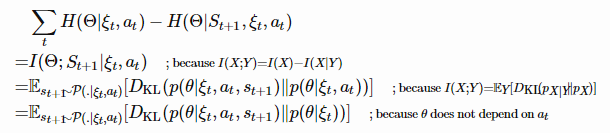
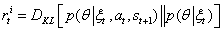 。
。
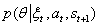 的计算通常比较困难。
的计算通常比较困难。
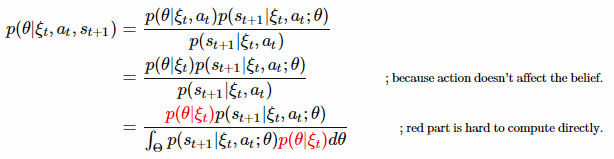 由于很难直接计算
由于很难直接计算
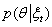 ,很自然地想到用另一个分布
,很自然地想到用另一个分布
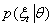 以及最小化
以及最小化
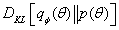 。
。
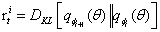
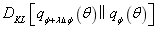 ,这很容易计算,因为
,这很容易计算,因为
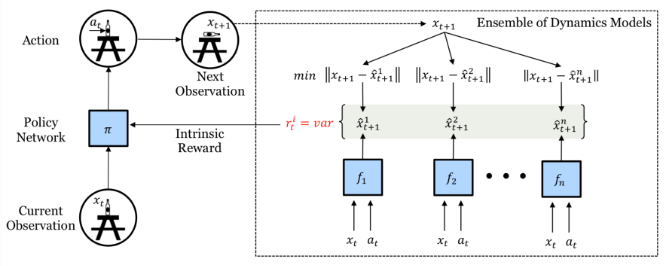
(2)
随机网络
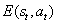 ,探索附加奖励记作
,探索附加奖励记作
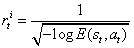 。
。
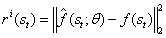 。
。
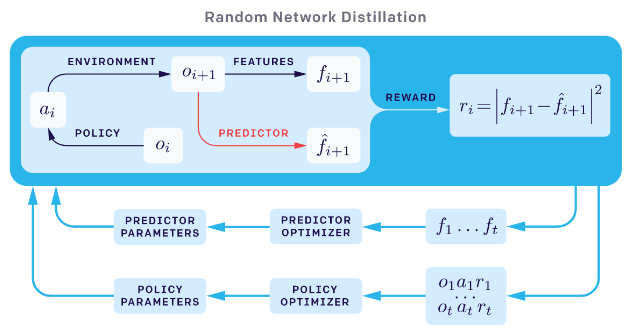
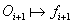 由固定的随机神经网络生成(图片来源:OpenAI博客:基于预测奖励的强化学习)
由固定的随机神经网络生成(图片来源:OpenAI博客:基于预测奖励的强化学习)
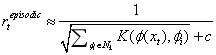
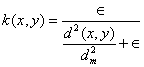
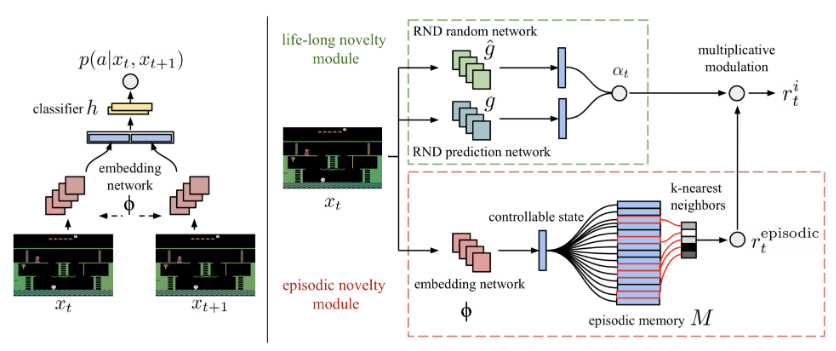
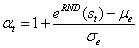 ,其中
,其中
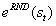 的平均值和标准差。
的平均值和标准差。
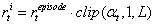 ,其中L是恒定的最大奖励标量。
,其中L是恒定的最大奖励标量。
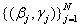 。回想一下,给定
。回想一下,给定
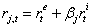 ,
,
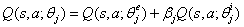 。在训练过程中,分别用奖励
。在训练过程中,分别用奖励
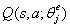 和
和
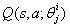 进行优化。
进行优化。
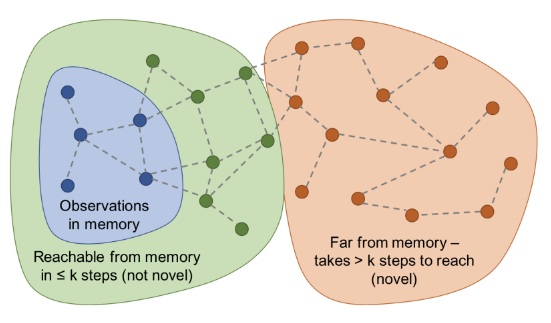
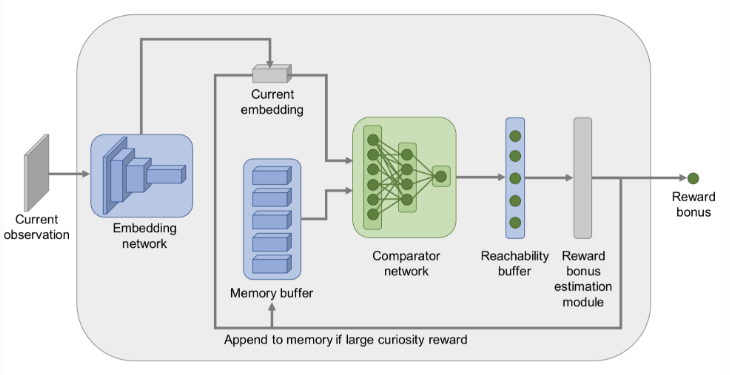
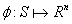 将状态编码为特征向量,接着利用比较器网络
将状态编码为特征向量,接着利用比较器网络
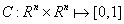 输出一个二进制标签,说明两个状态在状态转换图中是否足够接近(即在 k 步内可以到达),即
输出一个二进制标签,说明两个状态在状态转换图中是否足够接近(即在 k 步内可以到达),即
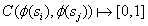 。
。
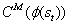 。探索附加奖励是
。探索附加奖励是
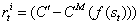 ,其中 C′ 是已确定的奖励符号的预定义阈值(例如,C′=0.5对于持续时间固定的情景非常有效)。当很难从内存缓冲区中的状态转移到新状态时,就给予这些新状态较高的附加奖励。
,其中 C′ 是已确定的奖励符号的预定义阈值(例如,C′=0.5对于持续时间固定的情景非常有效)。当很难从内存缓冲区中的状态转移到新状态时,就给予这些新状态较高的附加奖励。
2、定向探索
-
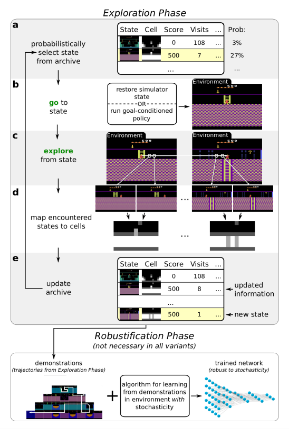
基于策略的定向探索是通过学习一个目标条件策略,利用该策略反复访问内存中的已知状态,而非简单地重置模拟器状态。依据先前内存中到达选定状态的最佳轨迹训练目标条件策略。为了从达成目标的轨迹中尽可能多地提取信息,策略网络的损失函数包括自我模仿学习(SIL;2018年论文《Self-Imitation Learning》提出)损失。 -
同样,他们发现当智能体回到最有可能完成任务的状态并继续探索时,基于策略采样的动作优于随机动作。 -
对基于策略的定向探索的另一处改进是可调整图像到单元的缩小功能。这样优化使内存中不会出现单元数目过多或过少的情况。


-
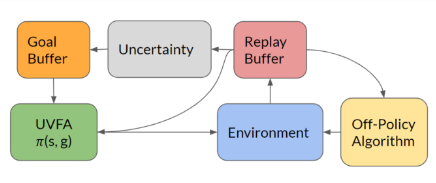
如果M是P=0.5的独立伯努利分布,则对应于双自引导或非自引导方法。 -
如果M总是返回一个全1掩码,则该算法将简化成一个集合方法。
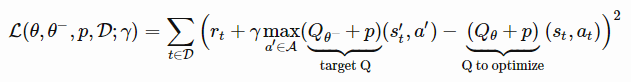
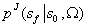 表示给定启动状态
表示给定启动状态
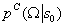 表示可以从中取样的选项的概率分布。根据定义有
表示可以从中取样的选项的概率分布。根据定义有
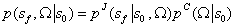 。
。
-
从 到最大化
获得一组不同的最终状态。
-
精确地知道给定选项Ω时哪个状态以最小化 结束。
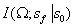 最大化:
最大化:
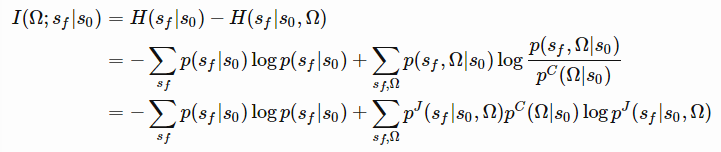
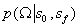 的值,用近似分布q代替。根据变分下限,将得到
的值,用近似分布q代替。根据变分下限,将得到
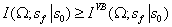 。
。

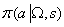 可以用任何RL算法进行优化。利用选项推理函数
可以用任何RL算法进行优化。利用选项推理函数
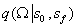 进行监督学习。先验概率
进行监督学习。先验概率
-
策略充当编码器,从噪声分布中提取环境信息并转换为轨迹。 -
解码器尝试从轨迹中恢复环境信息,并奖励使环境信息更易于区分的智能体策略。智能体的动作在训练过程中对解码器不可见,所以智能体必须以一种便于与解码器通信的方式与环境进行交互,以便更好地进行预测。此外,解码器在一个轨迹中循环地执行一系列步长值,以更好地模拟时间步长之间的相关性。
原文链接:
阅读原文,直达“ KDD”小组,了解更多会议信息!
登录查看更多