CS224W 7.2 Graph Representation Learning

上文我们已经学习了基于随机游走的图表示算法deepwalk.

CS224W 7.1 Graph Representation Learning

那么,有没有更好的随机游走策略来进一步提升deepwalk的效果呢,那就是Jure组的node2vec.

这里需要补充一个知识点，关于dfs（深度优先搜索）和bfs（广度优先搜索），我们之前提到random walk，在deep walk的算法中，random walk用的是dfs，所谓dfs，经常刷leetcode的人应该不陌生：

下文来自上面链接：https://blog.csdn.net/qq_37230495/article/details/88531697

广度优先搜索BFS

基本思想：首先访问起始顶点v，接着由v出发，依次访问v的各个未访问过的邻接顶点w1,w2,…,wi，然后再依次访问w1,w2,…,wi的所有未被访问过的邻接顶点；再从这些访问过的顶点出发，再访问它们所有未被访问过的邻接顶点……依次类推，直到图中所有顶点都被访问过为止。

通过下面的图，我们看看BFS是如何遍历的：

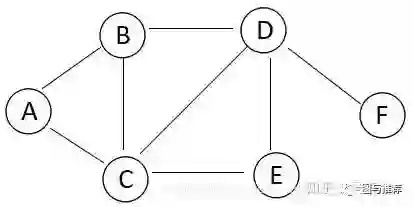
1.假设我们从A开始访问，这时候遍历的结果为A

2.A的邻接结点有B、C，我们先访问B、再访问C，这时候遍历的结果为A->B->C。

3.A的邻接结点已经访问完了，我们开始访问B结点的邻接结点，因为C已经被访问过，所以B的未被访问过的邻接结点只有D，这时候遍历的结果为A->B->C->D。

4.B的邻接结点已经访问完了，我们开始访问C结点的邻接结点，因为D已经被访问过，所以C的未被访问过的邻接结点只有E，这时候遍历的结果为A->B->C->D->E。

5.C的邻接结点全部被访问过，D的未被访问过的邻接结点只有F，因此最后遍历的结果为A->B->C->D->E->F。

从上面可以看出，广度优先搜索是一种分层的查找过程，每向前走一步可能访问一批顶点。

深度优先搜索DFS

基本思想：

首先访问图中某一起始顶点v，然后由v出发，访问与v邻接且未被访问的任一顶点w1，再访问与w1邻接且未被访问的任一顶点w2，……重复上述过程。当不能再继续向下访问时，依次退回到最近被访问的顶点，若它还有邻接顶点未被访问过，则从该点开始继续上述搜索过程，直到图中所有顶点均被访问过为止。

通过下面的图，我们看看DFS是如何实现遍历的：

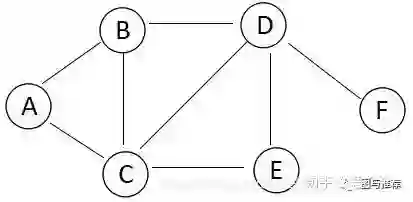
1.假设从A顶点出发，与A相邻的顶点有B和C，我们先访问B，这时候遍历的结果为：A->B。

2.再从B出发，与B相邻的顶点且未被访问过的顶点为C和D，我们先访问C，这时候遍历的结果为：A->B->C。

3.再从C出发，与C相邻的顶点且未被访问过的顶点为D和E，我们先访问D，这时候遍历的结果为：A->B->C->D。

4.再从D出发，与D相邻的顶点且未被访问过的顶点为E和F，我们先访问E，这时候遍历的结果为：A->B->C->D->E。

5.再从E出发，与E没有相邻的顶点，这时候，返回D，与D相邻的顶点且未被访问过的还有F，我们再访问F，此时所以的顶点都被访问完，遍历的结果为：A->B->C->D->E->F。

这种算法所遵循的搜索策略是尽可能“深”的搜索一个图。

另一种node embedding的算法：line使用的是bfs的搜索策略，不过这节课没有介绍，所以这里不详细介绍了，感兴趣的可以关注：

浅梦：【Graph Embedding】LINE：算法原理，实现和应用 zhuanlan.zhihu.com

这个大佬的专栏，写的非常详细，还有示例代码。。。太牛逼。

---

然后我们接下去看才不那么懵逼了；

首先明确目标：我们希望具有相似的网络结构的node在embedding空间中接近；

那么还是使用极大似然法来进行求解，并且独立于下游任务，因此还是使用无监督学习的方法来完成。

重要的发现：更加灵活的网络邻域节点的定义能够带来表达能力更强的node embedding结果。

我们不再像deepwalk那样使用dfs的策略来进行random walk，而是使用 biaesd second order random walk的策略来产生node u的领域节点。

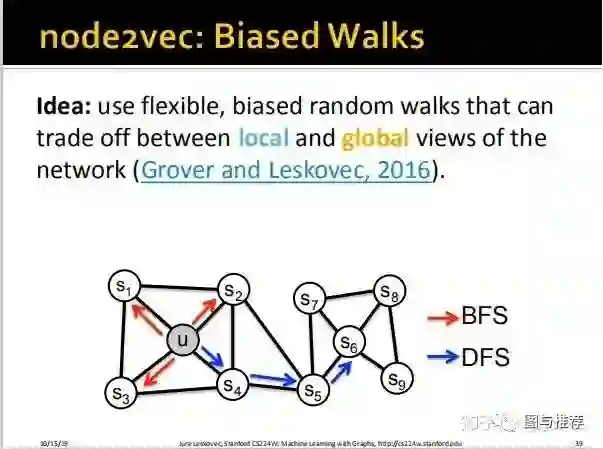
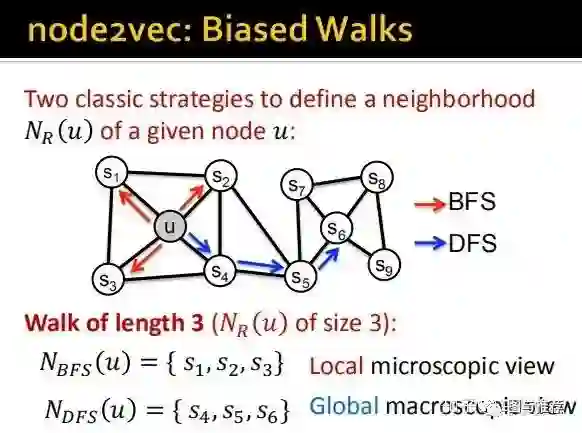
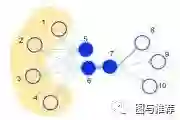
如上图，假设我们random walk的steps是3步，u节点使用的是bfs的搜索策略，那么比较容易就在其附近搜索完就了事儿了，从u开始只能搜索到s1、s2、s3，则只能捕捉到 local microscopic view（局部关联特征。。谷歌翻译很奇怪，这是自己意译的）

如果，而如果使用dfs的策略，则相对容易能够搜索到s4、s5、s6，但是却丧失了局部关联特征而丧失了 local microscopic view（全局关联特征），这说的是啥意思呢？

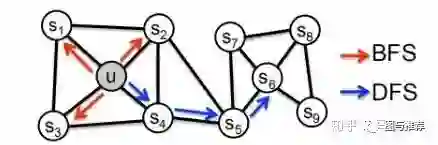
实际上是这样，如果我们使用deep walk，走的是蓝色这条线，捕获了全局关联特征，丧失了局部特征关联，那么如果我们还想要考虑局部关联特征怎么办？比如u和s6分别是左右两个社区的中心点，他们的网络结构是类似的，比如说不同的欺诈团伙，左边是A团伙，右边是B团伙，他们的组织结构类似，但是他们之间没有关联，可是他们的组织结构可能对于反欺诈的判别来说非常重要，那么这个时候我们就需要使用到bfs了，但是如果我们仅使用bfs，就顾此失彼了，比如另一个场景，欺诈分子之间关系都是非常密切，假设s4，s5，s6就是三个诈骗犯，一丘之貉，那么使用bfs的策略就无法cover到这种情况了。

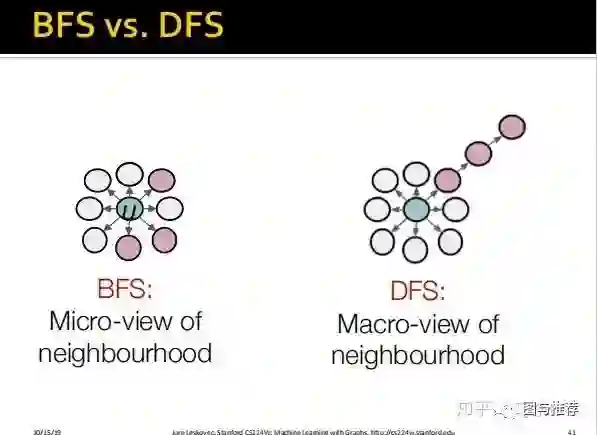
而现实的场景可能更加复杂，骗子之间可能是既是在深度上相互关联，也具有相似的社区结构，只不过可能有的时候其中一种情况的程度更深一点，另一种情况的程度更浅一代女，那么我们该如何解决这种问题？

答案就是讲二者通过权重的方式结合起来，我们引入了一种称为biased random walks的方法：

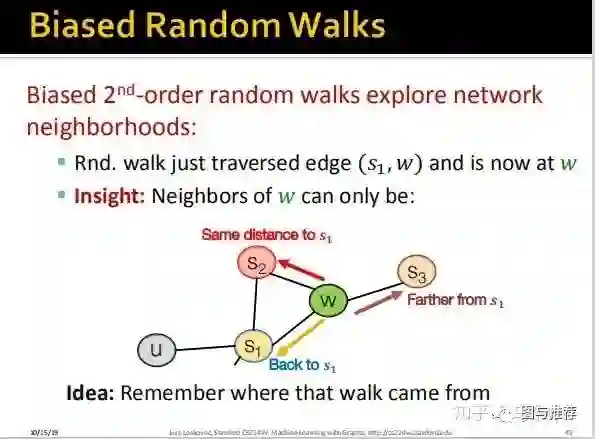
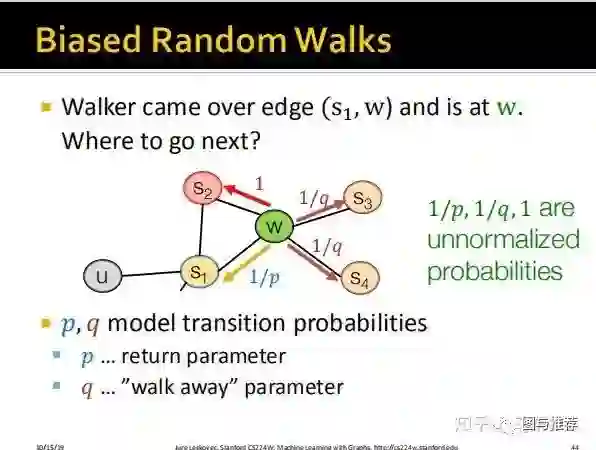
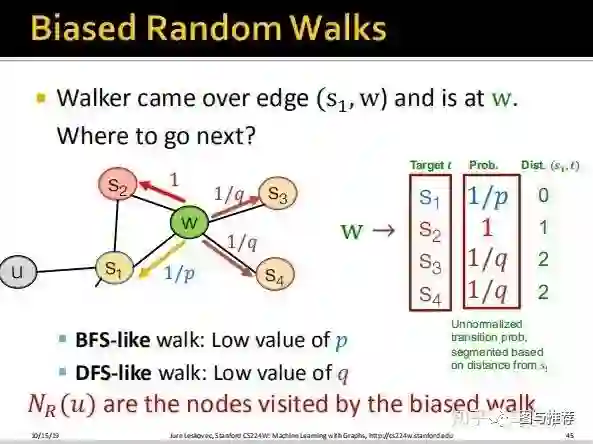
上图非常形象的解释了整个算法工作的流程。直接对照着最后一幅图讲也就是上面这幅图讲即可，假设我们从u出发到达s1，然后假设s1到达w（此时无论dfs、bfs都只能随机选择s2或者w，因为这个时候还没的选呢），此时我们陷入了决策，是使用bfs还是dfs继续搜索，如果使用bfs，则我们要从w到s2（因为bfs是先把访问到的节点所有的邻节点访问完，因为这里s2直接和w相连所以直接从w搜索到s2），如果使用dfs，则w可以访问s3或者s4（不访问s1的另节点）。可以看到上面定义了dist(s1,t)，t表示s1下一步要到达的节点。

这里定义了两个超参数p for bfs；

q for dfs；

这个时候引入了一个偏置函数：

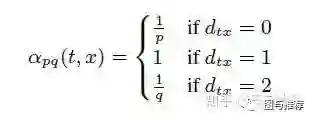
dist(s1,t)只有0，1，2三个取值：

1、如果w走向s3或者s4，显然是dfs的策略，因为此时s1的邻节点还没搜索完，则dist(s1,s3)=2，因为要经过s1和s3间隔了两个edge，对应的prob为1/q；

2、如果w走向s2，则是bfs的策略，dist(s1,s3)=1，对应的prob为1；

3、如果w回到了s1，则是bfs的策略，dist(s1,s1)=0，对应的prob为1/p;

其中p和q是人工指定的超参数，用户自己定义。

这样一来，就可以看出，超参数p控制的是重新访问原来结点的概率，也就是保守探索系数，而超参数q控制的是游走向更远方向的概率，也就是激进探索系数。如果q较大，那么游走策略则更偏向于广度优先策略，若q较小，则偏向于深度优先策略。

Ph0en1x：网络表示学习(一)--DeepWalk、LINE、Node2Vec、HARP、GraphGAN zhuanlan.zhihu.com

不过其实感觉这里不考虑dfs和bfs也是很好理解的，我们只要理解这个偏置函数就可以了；

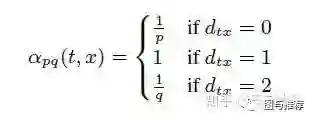
这样整个算法的流程大概就出来了。

不过在另一篇文章里面看到了更完整的描述。不过这里的算法步骤介绍的比较粗略，更加详细的算法推导过程可见：

浅梦：【Graph Embedding】node2vec：算法原理，实现和应用 zhuanlan.zhihu.com

这里介绍了如何使用embedding的结果。