优化 | 怎么判断一个优化问题是凸优化还是非凸优化？

加入极市专业CV交流群，与6000+来自腾讯，华为，百度，北大，清华，中科院等名企名校视觉开发者互动交流！更有机会与李开复老师等大牛群内互动！

同时提供每月大咖直播分享、真实项目需求对接、干货资讯汇总，行业技术交流。关注 极市平台 公众号 ，回复 加群，立刻申请入群~

---

本文介绍了判断一个优化问题是否是凸/非凸问题的常用方法：基于定义/一般形式判断；求导&一阶/二阶充要条件判断；基于叠加/变化/复合而成；基于定义的蒙特卡洛采样暴力数据验证。

一般来说，判断一个问题是否是凸的是强NP-难的

首先这个问题一般来说是很难的。比如：判断一个多元四次（及以上）偶多项式是否是凸的是strongly NP-hard的（http://web.mit.edu/~a_a_a/Public/Publications/convexity_nphard.pdf）。也就是说，除非NP=P，不存在（伪）多项式算法可以判断一个优化问题是凸或非凸的。

凸问题的一般形式

所以实际上难点就在于如何判断一个函数是否是凸的。

判断一个函数是否凸的一些“奇技淫巧”

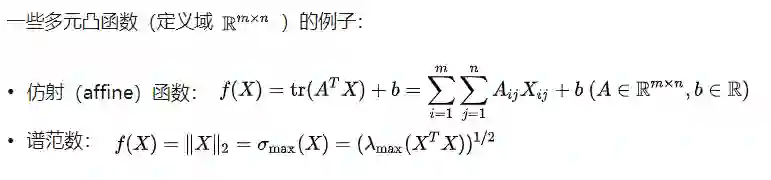
当然，如果这些方法都没用，我们还是只能回归初心（凸函数的定义），可以数值地来进行蒙特卡洛验证：每次取俩点，然后看凸组合的值是否小于等于值的凸组合...做很多很多次采样

以下sao操作来自于Stephen Boyd（我不背锅，来源是Boyd本人的凸优化公开课课程）：如果当你蒙特卡洛采样了很多很多次都没有发现反例，那么可以认为大概率这函数估计是凸的，这个时候你可以把它放在paper里作为“猜想”（conjecture），说不定过段时间某个年轻有为发奋向上的青年AP就写了个几十页proof把你的“猜想”给证明了 -- 这也是判断是否是凸函数的好方法233 （别人问你怎么想到这个conjecture的："Intuition."）

参考文献：

Boyd, Stephen, and Lieven Vandenberghe. Convex optimization. Cambridge university press, 2004.

-End-

*延伸阅读

• NIPS 2018 | 作为多目标优化的多任务学习：寻找帕累托最优解
  

• 40万现金大奖+免费算力+英特尔神经棒，极市开发者榜单邀你来战！

• 分析梯度下降的轨迹，更好地理解深度学习中的优化问题
  

添加极市小助手微信（ID : cv-mart），备注：研究方向-姓名-学校/公司-城市（如：目标检测-小极-北大-深圳），即可申请加入目标检测、目标跟踪、人脸、工业检测、医学影像、三维&SLAM、图像分割等极市技术交流群，更有每月大咖直播分享、真实项目需求对接、干货资讯汇总，行业技术交流，一起来让思想之光照的更远吧~

△长按添加极市小助手

△长按关注极市平台

觉得有用麻烦给个在看啦~