李沐：漫谈在线学习：在线梯度下降

2017 年 11 月 5 日 全球人工智能

在线凸优化

回顾下上次聊的专家问题，在 $t$ 时刻专家 $i$ 的损失是 $\ell_t(e^i)$ ，于是这个时刻Weighted Majority（WM）损失的期望是 $\sum_{i=1}^m w_t^i\ell_t(e^i)$ ，是关于这 $m$ 个专家的损失的一个线性组合（因为权重 $w_t^i$ 关于 $i$ 的和为1，所以实际上是在一个simplex上）。将专家在 $t$ 时刻的损失看成是这个时候进来的数据点，于是我们便在这里使用了一个线性的损失函数。

虽然WM的理论在上个世纪完成了[Littlestone 94, Freund 99]，将其理论拓展到一般的凸的函数还是在03年由Zinkevich完成的。当时Zinkevich还是CMU的学生，现在在Yahoo! Research。话说Yahoo! Research的learning相当强大，Alex Smola（kernel大佬），John Langford（有个非常著名的blog），这些年在large scale learning上工作很出色。

回到正题。我们提到在online learning中learner遭受的累计损失被记成 $\sum_{t=1}^T\ell_t(h_t)$ ，如果挑选 $h_t$ 的策略集 $\mathcal{H}$ 是凸的，而且损失函数 $\ell_t(h_t)$ 关于 $h_t$ 是凸的，那么我们称这个问题为Online Convex Optimization（OCP）。通常我们将 $h_t$ 表示成一个向量 $w_t$ ，例如WM中的维护的 $m$ 专家信任度，所以这时 $\mathcal{H}\subseteq\mathbb{R}^m$ 。

在线梯度下降

Zinkevich提出的算法很简单，在时刻 $t$ 做两步操作，首先利用当前得到数据对 $w_t$ 进行一次梯度下降得到 $w_{t+1}$ ，如果新的 $w_{t+1}$ 不在 $\mathcal{H}$ 中，那么将其投影进来：

$\displaystyle w_{t+1}=\Pi_{\mathcal{H}}(w_t-\eta_t\nabla\ell_t(w_t)),$ 这里 $\nabla\ell_t(w_t)$ 是 $\ell_t(w_t)$ 关于 $w_t$ 的导数（如果导数不唯一，就用次导数）， $\eta_t$ 是学习率， $\Pi_{\mathcal{H}}(w)$ 是投影子，其将不在 $\mathcal{H}$ 中的向量 $w$ 投影成一个与 $w$ 最近的但在 $\mathcal{H}$ 中的向量（如果 $w$ 已经在 $\mathcal{H}$ 中了，那就不做任何事），用公式表达就是 $\Pi_{\mathcal{H}}(w)=\arg\min_{u\in\mathcal{H}}\|w-u\|$ 。此算法通常被称之为 Online Gradient Descent。

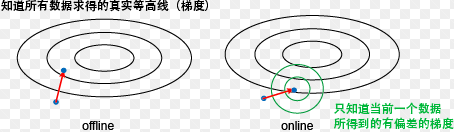
先来啰嗦几句其与离线梯度下降的区别。下图是一个区别示意图。在离线的情况下，我们知道所有数据，所以能计算得到整个目标函数的梯度，从而能朝最优解迈出坚实的一步。而在online设定下，我们只根据当前的数据来计算一个梯度，其很可能与真实目标函数的梯度有一定的偏差。我们只是减少 $\ell_t(w_t)$ ，而对别的项是否也是减少就难说了。当然，我们一直在朝目标前进，只是可能要走点弯路。

那online的优势在哪里呢？其关键是每走一步只需要看一下当前的一个数据，所以代价很小。而offline的算法每走一个要看下所有数据来算一个真实梯度，所以代价很大。假定有100个数据，offline走10步就到最优，而online要100步才能到。但这样offline需要看1000个数据，而online只要看100个数据，所以还是online代价小。

于是，我们很容易想到，offline的时候能不能每一步只随机抽几个数据点来算一个梯度呢？这样每一步代价就会很少，而且可能总代价会和online一样的少。当然可以！这被称之为Stochastic Gradient Descent，非常高效，下回再谈把。

在这里， $\mathcal{H}$ 的作用是什么呢？记得在learning中的目标函数通常是损失+罚（ $\ell(w)+\lambda \Omega(w)$ ）的形式。例如ridge regression就是平方误差+ $\ell_2$ 罚，lasso是平方误差+ $\ell_1$ 罚，SVM是hinge loss+ $\ell_2$ 罚。最小化这个目标函数可以等价于在 $\Omega(w)\le\delta$ 的限制下最小化 $\ell(w)$ 。 $\lambda$ 和 $\delta$ 是一一对应的关系。实际上 $\Omega(w)\le\delta$ 就是定义了一个凸子空间，例如使用 $\ell_2$ 罚，既 $\|w\|^2$ ，时就是一个半径为 $\delta$ 的球。所以，Online Gradient Descent可以online的解这一类目标函数，只是对于不同的罚要选择不同的投影子。

Regret Bound分析

记投影前的 $\tilde w_{t+1} = w_t-\eta_t\nabla\ell_t(w_t)$ ，以及offline最优解 $w^*=\arg\min_{w\in\mathcal{H}}\sum_{t=1}^T\ell_t(w)$ 。因为 $\mathcal{H}$ 是凸的且 $w^*$ 在其中，所以对 $\tilde w_{t+1}$ 投影只会减少其与 $w^*$ 的距离，既 $\|w_{t+1}-w^*\|\le\|\tilde w_{t+1}-w^*\|$ 。简记 $\nabla_t=\nabla \ell_t(w_t)$ ，注意到

$\displaystyle \|\tilde w_{t+1}-w^*\|^2=\|w_t-w^*\|^2+\eta_t^2\|\nabla_t\|^2-2\eta_t\langle\nabla_t,w_t-w^*\rangle.$

由于 $\ell_t$ 是凸的，所以有

$\displaystyle \ell_t(w_t)-\ell_t(w^*)\le \langle\nabla_t,w_t-w^*\rangle \le \frac{1}{2\eta_t}\big(\|w_t-w^*\|^2 - \|w_{t+1}-w^*\|^2\big) + \frac{\eta_t}{2}\|\nabla_t\|^2.$

取固定的 $\eta_t=\eta$ ，对 $t$ 进行累加就有 $R(T)\le \frac{1}{2\eta}\|w_1-w^*\|^2+\frac{\eta}{2}\sum_{t=1}^T\|\nabla_t\|^2$ 。记 $\mathcal{H}$ 的直径为 $D$ ，且对所有 $t$ 有 $\|\nabla_t\|\le L$ 成立（既Lipschitz常数为 $L$ ），再取 $\eta=\frac{D}{L\sqrt{T}}$ ，那么 $\displaystyle R(T)\le LD\sqrt{T}.$