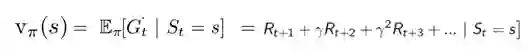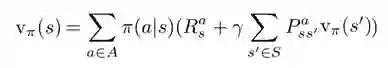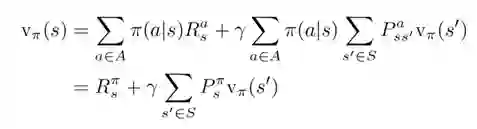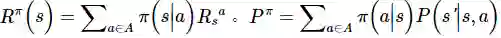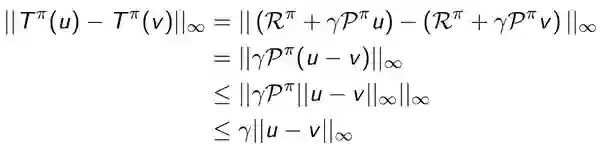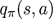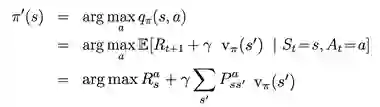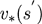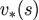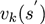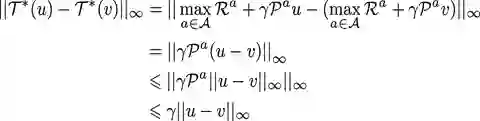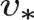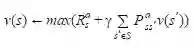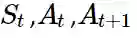MDP中的规划-CMU深度强化学习第三讲
产业 学术 趣玩
每周推送原创潮流机器人资讯
我们获得授权翻译CMU课程 10703 Deep Reinforcement Learning & Control,这是第三讲。
感谢Katerina Fragkiadaki教授的支持。
翻译贡献者:
李政锴,HIT,CSE (1-9)
罗瑞琨, (10-18)
张浩,蓝胖子机器人Dorabot, (19-30)
Shin, NUS, CS (31-38)
夏伟, UCAS, ML&AI (39-45)
XaoSHuan,TJU (46-51)
孔令志, (52-58)
组长:李政锴
「机器人学家」授权翻译
本讲
大纲
精确求解法
策略迭代(属于动态规划)
策略评估
策略改进
值迭代(属于动态规划)
线性规划
近似解法
异步动态规划
/********** 李政锴(1-9) **********/
确定性 VS 随机性策略
问:每个MDP(马氏决策过程)都有一个确定性的最优策略。那么为什么还要讨论随机策略呢?
答:一方面,进行探索需要采用随机动作(当将得到的收益和动态未知的时候)。另一方面,有时候RL要处理的问题并不是严格的MDP。比如下面的例子——猜拳。
MDPs VS 博弈(Games)
问:剪刀石头布有一个最优随机策略。为什么?
答:这不是MDP!在MDP中,环境动态特性被假设为符合马尔科夫链,即:下一个状态分布仅依赖于当前状态和动作,而非到目前为止的所有动作。
为了模拟对手可以针对我们目前的策略进行相应的调整,状态就应该被定义为自与对手博弈伊始的整个过程(whole episode),而非仅考虑当前时刻的状态。这不是一个有效的MDP定义方式,因为这种定义下问题没有状态更迭的过程。参考贝叶斯决策理论和博弈论(Bayesian Decision Making and Game Theory)。
有些博弈,如:围棋、西洋双陆棋,其状态属于马尔科夫链,此时适于应用MDP。考虑环境动态特性的情况下,求某一事件点的最值,就要使用back up diagrams。
问:西洋双陆棋MDP能否模拟对手针对我们对弈策略所做的相应调整?
答:不能。因为环境动态特性被假定为以状态为条件的马尔科夫链:下一个状态分布仅取决于当前状态和动作,而不是到目前为止的所有动作!对手的适应性调整过程不能得到模拟。
所以,对于已作讨论的MDP,环境变量可以包含对抗性信息,但是不具备适应性。
状态不确定性
问:对状态不确定性建模的原因是什么?
答:自动驾驶汽车不能确定探测到的是一个书包还是一个婴儿,这样的不确定性将触发走近并检查的信号。该问题的求解可以通过对状态进行随机性建模或确定性建模,这里所指的状态是:我的认知存在不确定性,并且需要采用确定性动作来解决待查明的隐藏状态:那是个书包,继而以相同速度继续前进;或者那是个婴儿,继而减速。在此,解决不确定性采用的确定性方法就是指“走近一些”。
奖励
奖励可能取决于智能体转移前的状态,或转移后的状态,或执行过的动作,或三者的综合。在我们的表述中,奖励不取决于转移后的状态。

回顾:当奖励取决于先前的状态和动作时,

思考:当奖励取决于下一个状态时,
MDP
求解
预测=给定一个MDP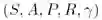
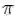
最优控制=给定一个MDP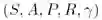
我们仍然考虑已知动态和奖励的有限MDP(有限指状态和动作的离散且有限集)。
/********** 罗瑞琨(10-18) **********/
下面我们介绍精确求解MDP的方法。第一种方法就是策略迭代(Policy Iteration)。它分为两步:策略评估(Policy Evaluation)和策略改进(Policy Improvement)。
策略评估:对于给定的策略π, 计算状态价值函数vπ.
状态价值函数v(s)的定义为:
状态价值函数v(s)的Bellman方程如下, 这是一个|S|元方程组,|S|为状态空间S中状态的数量。
从MDPs到MRPs
当我们固定一个策略时,MDP问题就变成了马尔科夫奖励过程(Markov Reward Process,下简写为MRP)。
由前面提到的状态价值函数的Bellman方程我们可以得到:
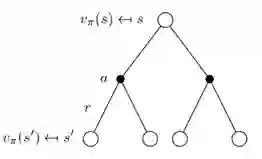
状态值函数的back up图
下图展示了策略评估的计算顺序。图中的空心圆圈表示的状态s,黑点表示的是动作a。这里我们使用Bellman方程,用一个状态周围的其他状态的价值来更新这个状态的价值,这种计算方法称为back up。因为使用的其他状态的价值仍是之前状态函数里的值,所以这种方法叫做back up。
MRP的状态价值函数Back up 图
如前面提到的,在给定的策略下,MDP会变成MRP。这样我们可以得到新的Back up图如下。如前面给出的公式所示,在MRP中,我们已经用给定的策略将动作a计算掉了(期望)。这样得到的新的Back up图中就不需要黑点来表示动作了。
矩阵形式
使用MRP,可以得到更加简洁的Bellman期望公式。如果有N个状态s,那么在策略评估的过程中,需要求解N个未知量(v(s)),有N个线性方程(每个状态有一个Bellman equation),这样可以得到一个N维线性系统,理论上可以直接求解。对这个N维线性系统可以得到如下的矩阵形式的表达。
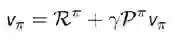
其中v为向量表示的状态价值函数,向量中的每一个元素表示对应状态的价值。R为向量表示的即时收益的期望,
得到解析解如下:
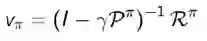
计算复杂度为O(N^3).
迭代法
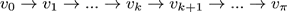
如上所示是一次“扫略(sweep)”。一次扫略完成对所有状态的backup操作。
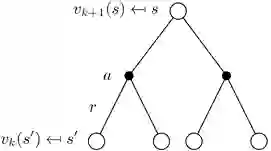
一个完整的策略评估backup:
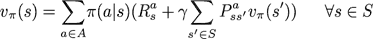
上式对应了前文的状态价值函数backup图,相似的可以得到状态价值函数迭代更新方法:
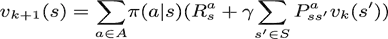
/********** 张浩 (19-30) START**********/
例子:小网格寻路问题
智能体在4x4方格里,每个方格有自己的编号。可以采用的动作是上下左右移动,任何动作的奖励都是-1,直到终止状态(图中首尾两个阴影方格),故该问题寻找最优策略以尽快到达终止状态。将agent带出方格的行为不会对态进行改变。
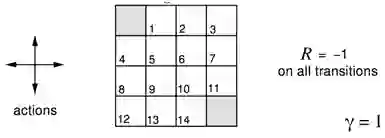
无折扣的周期任务
非终止状态:1,2,...,14;
终止状态(灰色方块,出现了两次)
会将智能体移出栅格的动作并不改变状态
直到终止状态之前,所有动作的收益都是-1
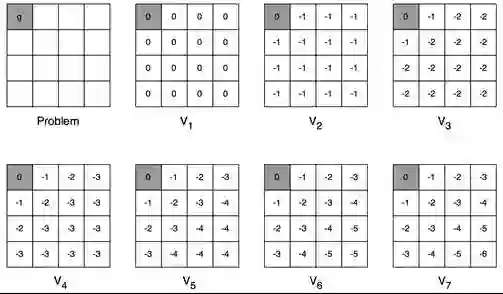
小网格问题的迭代策略评估
𝝅=同等概率的随机动作选择。下图中所示为对该策略的价值计算结果:
迭代策略评估算法
输入需要评价的策略𝝅
对于所有的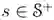
重复
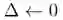
对于每个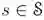
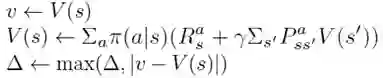
直到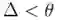
输出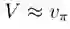
一个有|S|个状态的MDP,其所有价值函数V(s)构成的向量可以看成|S|维向量空间V中的一个点。要说明收敛性,就要说明策略评估里的计算——贝尔曼 backup 会对该空间中的点带来怎样变化?
下面我们说明,它每次迭代都会使这些点离得更近
所以贝尔曼backup在无穷次迭代后必然收敛到唯一解
价值函数的无穷范数(∞-Norm)
我们可以用∞-Norm来度量状态-价值函数u和v
即,两个状态价值之间的距离。
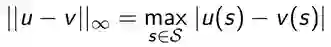
贝尔曼Back up是收缩的
定义贝尔曼Back up操作子T𝝅
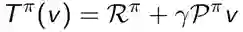
这个操作子是𝛄-收缩的,即它会使价值函数之间的距离至少缩小到原来的𝛄倍。𝛄是定义价值时的折扣系数,小于1:
收缩映射定理
定理(收缩映射定理)
已知T是𝛄收缩,对于操作T(v)下的任意完备(即闭合)的度量空间V,有:
T以线性收敛速率𝛄收敛到唯一的固定点
(编者注:即策略评估一定会收敛到一个值)
结论:迭代策略评估是收敛的
贝尔曼期望操作子T𝝅有唯一的固定点。(根据贝尔曼期望方程)v𝝅是T𝝅上的一个固定点,所以根据收缩映射定理,迭代策略评估收敛于v𝝅
/********** Shin(31-38) **********/
在衡量了当前策略π的价值vπ后,下一步要考虑的是如何改进策略。
对于一个给定的状态s, 做另一个动作a≠π(s)会不会更好?
当且仅当
的时候,动作a才会更好。
并且,我们可以从vπ中计算
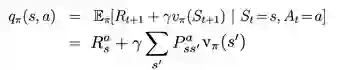
像这样对每一个状态都进行计算,我们便可以得到一个新的策略
如果策略并没有因此改变,那么就说明现有的策略已经是最优了。

(编者注:策略迭代就是在反复进行策略评估和策略改进。)
伪代码:
1. 初始化

2. 策略评估
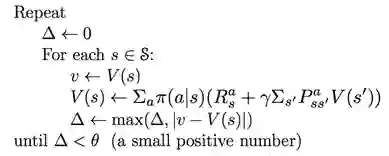
3. 策略改进
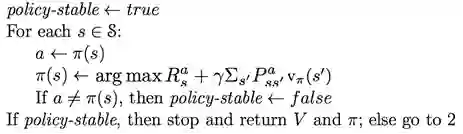
例子:小网格中的策略迭代评估
我们仍然以一个等概率随机策略为例。
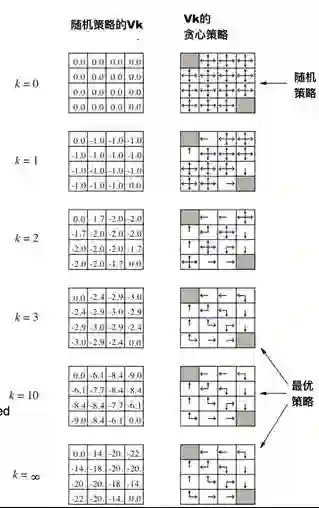
(编者注:上图中在Value完全收敛之前就已经得到了最优策略,所以可能我们不需要把策略评估算的特别仔细)
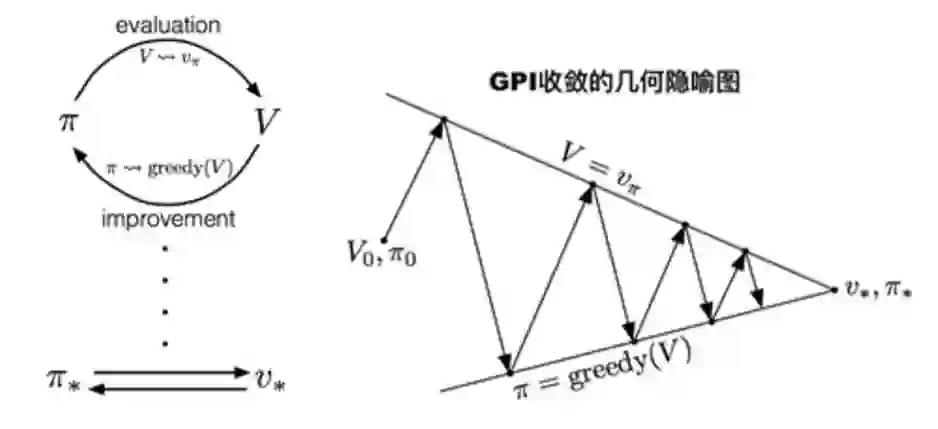
广义策略迭代(GPI)
策略评估是否需要收敛到vπ ?
或者我们是不是应该设定一个停止条件,比如值函数ϵ收敛?
或者在k次迭代评估之后直接停止?比如在小网格中k=3已经能够达到最优策略了。
这让我们思考,也许可以每次迭代都更新策略——这相当于值迭代(下一章节)。
广义策略迭代考虑的就是迭代评估、更新的各种可能性。
(编者注:我们可以自行选择每次迭代里进行多少策略评估和策略改进)
/**********夏伟(39-45)**********/
最优性原理
称策略 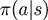

对于从状态s可以到达任意的状态s’
策略π也在状态s’处获得最优值,即
值
迭代
NOTE: 状态传递方向 
假设已知子问题的解为
;
原问题的解
可以通过一步前瞻(one-step lookahead)得到,即
.
值迭代的思想在于采用以上两个步骤重复更新迭代;
直观解释:从最后的收益(进入终态时)开始,不断反向(向前)更新(work backwarks)
仍然处于可多次循环遍历、随机MDP的工作范畴。
最短路径的例子
Note:g是终态。
问题:寻找最优策略π
解决方法:反复运用贝尔曼最优Backup(Bellman optimality backup)
可形式化为:
伪代码描述(采用同步备份):
在每一次迭代
对所有的状态
, 根据
更新
。
示意图如下,白圆圈为状态state,黑圆圈为动作action。
下面说明,贝尔曼最优backup是不断变优的(即往最优方向收缩)。
定义贝尔曼最优backup操作
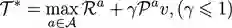
此操作是按照

贝尔曼最优backup操作
具有唯一的不动点
最优值函数
就是这个不动点(通过贝尔曼最优等式可以得到)
通过压缩映射原理的收敛性可以证明值迭代收敛于
.
/**********XaoSHuan(45-51)**********/
算法 |
解决的问题 |
算法依据 |
迭代策略评价
|
预测 |
贝尔曼期望方程 |
策略迭代
|
控制 |
贝尔曼期望方程+贪心策略改进 |
价值迭代
|
控制 |
贝尔曼最优化方程 |
复杂度分析:
求状态-价值函数 V(S)的算法,m个动作,n个状态时,每次迭代复杂度为:O(mn2)
求动作-价值函数Q(S,a)的算法,m个动作,n个状态时每次迭代复杂度:O(m2n2)
动态规划的效率问题
计算最优策略的算法复杂度是关于状态数目的多项式级,还算可以。
问题在于状态的 个数通常非常巨大,随着问题维度的增加而指数型增长(维数灾难)。
实际应用中,经典的动态规划可以应用在有几百万个状态的问题中。
异步
动态规划
目前我们所讲的动态规划方法都需要遍历整个状态集。
异步动态规划不需要全部遍历。它工作方式如下:
循环 直到满足收敛条件
任意选择一个状态,应用合适的方法backup状态值
仍然需要大量计算 ,但是避免了永无止境的遍历
我们可以智能地选择要backup的状态?可以!智能体可以借助其经验作为指导。
三种简单的异步动态规划方法:
In-place动态规划
依据优先级的动态规划
实时动态规划
In-place动态规划
同步动态规划的价值迭代保存两份价值函数副本:
对S中所有的状态s:

而In-place仅仅保存一份价值函数副本,更新的值立即被周围状态的backup使用:
对S中所有的状态s:
依据优先级的动态规划
用贝尔曼误差大小指导状态选择,如:
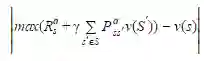
优先backup有最大Bellman误差的状态
在每次backup后,更新受到影响的状态的贝尔曼误差
需要已知逆模型
通过维护一个优先级序列,可以更有效的实现此算法
实时动态规划
思路: 只选择与智能体当前任务密切相关的状态
借助智能体的经验来指导选择状态
在每步之后获得
Backup状态 st:
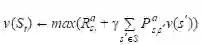
/**********孔令志(52-58)**********/
用采样Backup
在后续课程中,我们将考虑一些使用采用得到的估计值来backup的方法。
借助采样获得的收益和状态跳转 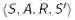
优势:
无需模型:不需要MDP的先验知识
通过采样降低维度灾难的风险
每次backup计算成本是恒定的,独立于问题规模。
近似动态规划
近似价值函数
用一个已知形式的函数v’去近似价值函数v
用动态规划去得到v’的参数
(编者注:当状态太多时,为每个状态分配一个变量会使得问题规模太大。一种解决的思路是,用一个参数化的函数去近似value function,然后RL问题就变成了一个参数估计问题。第7讲开始介绍。)
贝尔曼方程
的LP形式
线性规划(Linear programming, LP) 角度理解贝尔曼最优方程
回顾前文,在价值迭代时,我们实际上是在求解贝尔曼方程构成的方程组:
这可以表示成一个线性规划问题:
定理:上述优化问题的解,就是对应MDP的解。
定理证明
将贝尔曼方程的操作记为F,即:
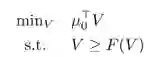
LP的任意解都满足V>=F(V)。下面说明,V>=F(V)即说明V=V*.
首先因为F是单调递增的,因此如果V>=F(V),就有F(V)>=F(F(V)),通过重复应用上述关系,有:
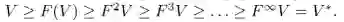
也即V=V*。
对偶问题-引出Q
这个线性规划问题的对偶问题有如下形式:

其目标函数是在取预期奖励的折扣总数的最大值。
其约束正好说明了,对偶变量
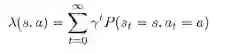
正是我们的动作价值函数Q(s,a)。
(本讲完)
编者注:深度增强学习正处在一个快速发展、迈向应用的时期。它在许多问题上取得了巨大成功,在另一些问题(比如实物的控制问题)上仍面临挑战。不论如何,了解学习这一工具是对机器人专业朋友们很有价值的一件事。
我们的翻译志愿者团队已经超过80人,整个学期的课件每份都已经至少有三人次负责,我们会尽力保证翻译质量。第四五六讲课件已经在翻译中。
CMU 10703 课程网站有更新,请点击阅读原文访问。
英文原版课件下载:请在后台回复“10703”获取下载链接。
本文由微信公众号 机器人学家 编译+整理成文。
转载请联系我们获得许可即可,不尊重作者劳动成果的行为会被举报。
手机长按下图二维码即可关注。