【DeepMind 公开课-深度强化学习教程代码实战01】迭代法评估4*4方格世界下的随机策略

2017 年 10 月 23 日 专知叶强

点击上方“专知”关注获取更多AI知识!

【导读】Google DeepMind在Nature上发表最新论文，介绍了迄今最强最新的版本AlphaGo Zero，不使用人类先验知识，使用纯强化学习，将价值网络和策略网络整合为一个架构，3天训练后就以100比0击败了上一版本的AlphaGo。Alpha Zero的背后核心技术是深度强化学习，为此，专知有幸邀请到叶强博士根据DeepMind AlphaGo的研究人员David Silver《深度强化学习》视频公开课进行创作的中文学习笔记，在专知发布推荐给大家！（关注专知公众号，获取强化学习pdf资料，详情文章末尾查看！）

叶博士创作的David Silver的《强化学习》学习笔记包括以下：

笔记序言：【教程】AlphaGo Zero 核心技术 - David Silver深度强化学习课程中文学习笔记

《强化学习》第一讲简介
《强化学习》第二讲马尔科夫决策过程
《强化学习》第三讲动态规划寻找最优策略
《强化学习》第四讲不基于模型的预测
《强化学习》第五讲不基于模型的控制
《强化学习》第六讲价值函数的近似表示
《强化学习》第七讲策略梯度
《强化学习》第八讲整合学习与规划
《强化学习》第九讲探索与利用

以及包括也叶博士独家创作的强化学习实践系列！

强化学习实践一迭代法评估4*4方格世界下的随机策略
强化学习实践二理解gym的建模思想
强化学习实践三编写通用的格子世界环境类
强化学习实践四 Agent类和SARSA算法实现
强化学习实践五 SARSA(λ)算法实现
强化学习实践六给Agent添加记忆功能
强化学习实践七 DQN的实现

本实战针对教程第四讲，欢迎查看！:

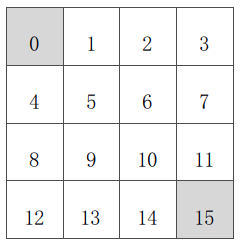
本篇用代码演示《强化学习》第三讲中的示例——方格世界，即用动态规划算法通过迭代计算来评估4*4方格世界中的一个随机策略。具体问题是这样：

已知（如上图）：

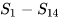
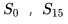
状态空间 S：为非终止状态；终止状态，图中灰色方格所示两个位置；

行为空间 A：{n, e, s, w} 对于任何非终止状态可以有向北、东、南、西移动四个行为；
转移概率 P：任何试图离开方格世界的动作其位置将不会发生改变，其余条件下将100%地转移到动作指向的位置；
即时奖励 R：任何在非终止状态间的转移得到的即时奖励均为-1，进入终止状态即时奖励为0；
衰减系数 γ：1；

当前策略π：个体采用随机行动策略，在任何一个非终止状态下有均等的几率往任意可能的方向移动，即π(n|•) = π(e|•) = π(s|•) = π(w|•) = 1/4。

问题：评估在这个方格世界里给定的策略。

该问题等同于：求解该方格世界在给定策略下的（状态）价值函数，也就是求解在给定策略下，该方格世界里每一个状态的价值。

我们使用Python编写代码解决该问题。

声明状态

states = [i for i in range(16)]

声明状态价值，并初始化各状态价值为0

values = [0  for _ in range(16)]

声明行为空间

actions = ["n", "e", "s", "w"]

结合方格世界的布局特点，简易声明行为对状态的改变

ds_actions = {"n": -4, "e": 1, "s": 4, "w": -1}

声明衰减系数为1

gamma = 1.00

根据当前状态和行为确定下一状态

def nextState(s, a):
  next_state = s
  if (s%4 == 0 and a == "w") or (s<4 and a == "n") or \     ((s+1)%4 == 0 and a == "e") or (s > 11 and a == "s"):
    pass
  else:
    ds = ds_actions[a]
    next_state = s + ds
  return next_state

得到某一状态的即时奖励

def rewardOf(s):
  return 0 if s in [0,15] else -1

判断某一状态是否为终止状态

def isTerminateState(s):
  return s in [0,15]

获取某一状态的所有可能的后继状态

def getSuccessors(s):
  successors = []
  if isTerminateState(s):
    return successors
  for a in actions:
    next_state = nextState(s, a)
    # if s != next_state:
    successors.append(next_state)
  return successors

根据后继状态的价值更新某一状态的价值

def updateValue(s):
  sucessors = getSuccessors(s)
  newValue = 0  # values[s]
  num = 4       # len(successors)
  reward = rewardOf(s)
  for next_state in sucessors:
    newValue += 1.00/num * (reward + gamma * values[next_state])
  return newValue

进行一次迭代

def performOneIteration():
  newValues = [0 for _ in range(16)]
  for s in states:
    newValues[s] = updateValue(s)
  global values
  values = newValues
  printValue(values)

辅助函数输出状态价值

def printValue(v):
  for i in range(16):
    print('{0:>6.2f}'.format(v[i]),end = " ")
    if (i+1)%4 == 0:
      print("")
  print()

主函数

def main():
  max_iterate_times = 160
  cur_iterate_times = 0
  while cur_iterate_times <= max_iterate_times:
    print("Iterate No.{0}".format(cur_iterate_times))
    performOneIteration()
    cur_iterate_times += 1
  printValue(values)

由于事先知道该算法将在150次左右收敛，我们将最大迭代次数设为了160，最后得到的价值函数如下：

The value function converges to:
 0.00  -14.00 -20.00 -22.00 -14.00 -18.00 -20.00 -20.00 -20.00 -20.00 -18.00 -14.00 -22.00 -20.00 -14.00   0.00 At Iterate No.153

从以上代码我们可以看出，我们设置了一个获取某一状态所有后续可能状态的集合这么一个方法，这就是体现动态规划算法思想的地方。如果无法获取一个状态的所有可能后续状态，那么就不能使用动态规划算法来求解。此外，我们使用的是异步更新价值的方法，即某一时刻状态的价值由前一时刻状态价值来计算。

完整的Python代码如下：

'''Implementation of small grid world example illustrated by David Silverin his Reinforcement Learning Lecture3 - Planning by Dynamic Programming. Author: Qiang YeDate: July 1, 2017The value function converges to: 0.00 -14.00 -20.00 -22.00 -14.00 -18.00 -20.00 -20.00 -20.00 -20.00 -18.00 -14.00 -22.00 -20.00 -14.00   0.00 At Iterate No.153'''# id of the states, 0 and 15 are terminal statesstates = [i for i in range(16)]#  0* 1  2   3  #  4  5  6   7#  8  9  10  11#  12 13 14  15*# initial values of statesvalues = [0  for _ in range(16)]# Actionactions = ["n", "e", "s", "w"]# 行为对应的状态改变量# use a dictionary for convenient computation of next state id.ds_actions = {"n": -4, "e": 1, "s": 4, "w": -1}  # discount factorgamma = 1.00# 根据当前状态和采取的行为计算下一个状态id以及得到的即时奖励def nextState(s, a):
  next_state = s
  if (s%4 == 0 and a == "w") or (s<4 and a == "n") or \     ((s+1)%4 == 0 and a == "e") or (s > 11 and a == "s"):
    pass
  else:
    ds = ds_actions[a]
    next_state = s + ds
  return next_state# reward of a statedef rewardOf(s):
  return 0 if s in [0,15] else -1# check if a state is terminate statedef isTerminateState(s):
  return s in [0,15]# get successor states of a given state sdef getSuccessors(s):
  successors = []
  if isTerminateState(s):
    return successors
  for a in actions:
    next_state = nextState(s, a)
    # if s != next_state:
    successors.append(next_state)
  return successors# update the value of state sdef updateValue(s):
  sucessors = getSuccessors(s)
  newValue = 0  # values[s]
  num = 4       # len(successors)
  reward = rewardOf(s)
  for next_state in sucessors:
    newValue += 1.00/num * (reward + gamma * values[next_state])
  return newValue# perform one-step iterationdef performOneIteration():
  newValues = [0 for _ in range(16)]
  for s in states:
    newValues[s] = updateValue(s)
  global values
  values = newValues
  printValue(values)# show some array info of the small grid worlddef printValue(v):
  for i in range(16):
    print('{0:>6.2f}'.format(v[i]),end = " ")
    if (i+1)%4 == 0:
      print("")
  print()# test functiondef test():
  printValue(states)
  printValue(values)
  for s in states:
    reward = rewardOf(s)
    for a in actions:
      next_state = nextState(s, a)
      print("({0}, {1}) -> {2}, with reward {3}".format(s, a,next_state, reward))

  for i in range(200):
    performOneIteration()
    printValue(values)def main():
  max_iterate_times = 160
  cur_iterate_times = 0
  while cur_iterate_times <= max_iterate_times:
    print("Iterate No.{0}".format(cur_iterate_times))
    performOneIteration()
    cur_iterate_times += 1
  printValue(values)if __name__ == '__main__':
  main()