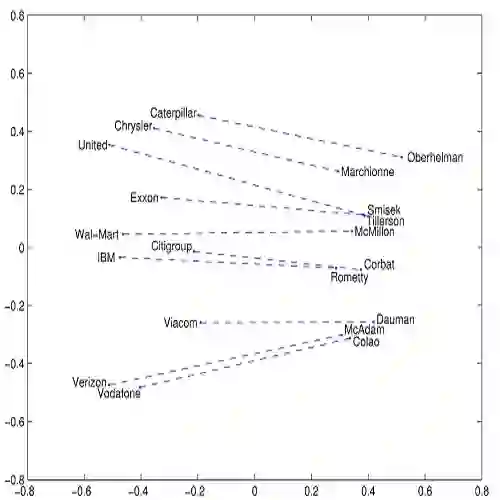
用线性规划去计算句子之间的相似度

2017 年 12 月 27 日 AI研习社 何史提

本文原载于知乎「Data Science with R&Python」专栏，AI 研习社获其作者何史提授权转载。

Word2Vec 或 FastText 之类的字嵌入模型已经被自然语言处理的人员广泛使用，原因无他，因为这些模型把所需要的维度降低了许多（用 bag-of-words 模型要和词典数相等的维度，但这类模型的维度只是在数百之间），而且字的相似度有更好的理解（用 bag-of-words 模型，字义相似的字都被视为不同，但这类模型字义相似的字都可用 cosine 相似度描述）。

那麽，如何用这些模型去描述句子之间的相似度？直接的方法就是把每一句子的每一个字加起来，然后计算 cosine 相似度。但这方法有点粗略，如果有些字加起来抵消了某些字义，那不太好。在 2015 年，Kusner 发表了一篇论文去解决这个问题，而这方法一个大好处就是他像距离或相似度一样是无需训练的，这方法叫作 Word Mover’s Distance (WMD)，可以说是 Earth Mover’s Distance 或 Wasserstein Distance 的一个特例。

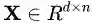
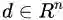
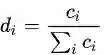
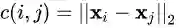
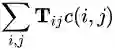
WMD 的定义很漂亮。假设字篏入模型标示为，当中 d 是字篏入模型维度， n 是字数。每一句子由一个 normalized BOW 向量表示，而，而 i 代表每一个字。字和字之间的距离是模型中的欧氏距离，， i 和 j 代表不同的字。我们想要计算的 WMD 就是。

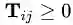
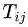
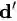
当中 T 是一个 n×n的矩阵，，每一个代表由第一句子的字 i 到第二句子字 j 的部分。（第二句子的 normalized BOW 向量是。）

这个问题的关键在于解 T ，而我们想把 WMD 降到最低，所以这也是一个最优化的问题： ,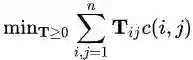

条件：。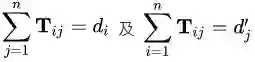

很明显地，这是一个綫性规划（linear programming）的问题。

在 Python 中，有很多最优化的包，其实 scipy 本身也自带一个优化器，但不合用；我也考虑过 cvxopt，但因为一些原因使程序变得混乱；到最后，我选择了 PuLP，然后我发现这个是最合适的工具。

先载入所需要的包：

from itertools import product
from collections import defaultdict

import numpy as np
from scipy.spatial.distance import euclideap
import pulp
import gensim

然后建一个函数，计算一个句子的 normalized BOW 向量：

def tokens_to_fracdict(tokens):    cntdict = defaultdict(lambda : 0)    for token in tokens:        cntdict[token] += 1    totalcnt = sum(cntdict.values())    return {token: float(cnt)/totalcnt for token, cnt in cntdict.items()}

以下就是最核心的程序：

def word_mover_distance_probspec(first_sent_tokens, second_sent_tokens, wvmodel, lpFile=None):    all_tokens = list(set(first_sent_tokens+second_sent_tokens))    wordvecs = {token: wvmodel[token] for token in all_tokens}    first_sent_buckets = tokens_to_fracdict(first_sent_tokens)    second_sent_buckets = tokens_to_fracdict(second_sent_tokens)    T = pulp.LpVariable.dicts('T_matrix', list(product(all_tokens, all_tokens)), lowBound=0)    prob = pulp.LpProblem('WMD', sense=pulp.LpMinimize)    prob += pulp.lpSum([T[token1, token2]*euclidean(wordvecs[token1], wordvecs[token2])                        for token1, token2 in product(all_tokens, all_tokens)])    for token2 in second_sent_buckets:        prob += pulp.lpSum([T[token1, token2] for token1 in first_sent_buckets])==second_sent_buckets[token2]    for token1 in first_sent_buckets:        prob += pulp.lpSum([T[token1, token2] for token2 in second_sent_buckets])==first_sent_buckets[token1]    if lpFile!=None:        prob.writeLP(lpFile)    prob.solve()    return prob

其中 wvmodel 是 Word2Vec 模型，去载入模型，用：

wvmodel = gensim.models.KeyedVectors.load_word2vec_format('/path/to/GoogleNews-vectors-negative300.bin.gz', binary=True)

（读者其实也可以用 FastText 或 Poincare Embedding，载入的函数不一样，但不影响以下的代码。FastText: gensim.models.wrappers.FastText.load_fasttext_format；Poincare:gensim.models.poincare.PoincareKeyedVectors.load_word2vec_format）

可以看到，使用 PuLP，要先定义一个 LpProblem，然后把成本函数和所有条件都加进去，最后用 LpProblem 的 solve() 方法去解决。读出我们想要的 WMD，可用 pulp.value(prob.objective)，但我们用以下的代码展示我们可如何读出各个参数和变量：

prob = word_mover_distance_probspec(['President', 'talk', 'Chicago'], ['Presidents', 'speech', 'Illinois'], wvmodel)
print(pulp.value(prob.objective))
for v in prob.variables():    if v.varValue!=0:        print(v.name, '=', v.varValue)

然后可得

2.88587622936 ("T_matrix_('Chicago',_'Illinois')", '=', 0.33333333) ("T_matrix_('President',_'Presidents')", '=', 0.33333333) ("T_matrix_('talk',_'speech')", '=', 0.33333333)

第一行就是 WMD，其他则是 T 的元素的量。其他例子：

document1 = physician, assistant
document2 = doctor
WMD = 2.8760048151
document1 = physician, assistant
document2 = doctor, assistant
WMD = 1.00465738773
document1 = doctors, assistant
document2 = doctor, assistant
WMD = 1.02825379372
document1 = doctor, assistant
document2 = doctor, assistant
WMD = 0.0

读者可参考此 Jupyter Notebook: http://t.cn/RHcJLky https://

其实，Python 包 shorttext 已经实现了这个方法，安装后，使用方法如下：

from shorttext.metrics.wasserstein import word_mover_distance
from shorttext.utils import load_word2vec_model

wvmodel = load_word2vec_model('/path/to/model_file.bin')

print word_mover_distance(['police', 'station'], ['policeman'], wvmodel)
                      # gives 3.060708999633789
print word_mover_distance(['physician', 'assistant'], ['doctor', 'assistants'], wvmodel)
          # gives 2.276337146759033

读参这个 tutorial：Metrics - shorttext 0.5.9 documentation（http://t.cn/RHcJHKm ）

另外，gensim 提供的 Word2Vec 模型中，也供程序员计算 WMD，但用的是 SIFT，而且距离是曼哈顿距离而非欧氏距离，详情参见：gensim: topic modelling for humans（http://t.cn/RHcJuid ）

圖片來至：Matt Kusner, Yu Sun, Nicholas Kolkin, Kilian Weinberger, “From Word Embeddings To Document Distances,” Proceedings of the 32nd International Conference on Machine Learning, PMLR 37:957-966 (2015). [http://t.cn/RHcJDpq ]

延伸閱讀：

Kwan-Yuet Ho, “Word Mover’s Distance as a Linear Programming Problem,” Everything About Data Analytics, WordPress (2017). [http://t.cn/RHci4ZE ]
Matt Kusner, Yu Sun, Nicholas Kolkin, Kilian Weinberger, “From Word Embeddings To Document Distances,” Proceedings of the 32nd International Conference on Machine Learning, PMLR 37:957-966 (2015). [http://t.cn/RHcJDpq ]
Github: mkusner/wmd. [http://t.cn/RthCUOV ]
Kwan-Yuet Ho, “Toying with Word2Vec,” Everything About Data Analytics, WordPress (2015). [http://t.cn/RHciCU9 ]
Kwan-Yuet Ho, “On Wasserstein GAN,”Everything About Data Analytics, WordPress (2017). [http://t.cn/RHcimxH ]
Martin Arjovsky, Soumith Chintala, Léon Bottou, “Wasserstein GAN,” arXiv:1701.07875 (2017). [https://arxiv.org/abs/1701.07875 ]
Alison L. Gibbs, Francis Edward Su, “On Choosing and Bounding Probability Metrics,” arXiv:math/0209021 (2002) [https://arxiv.org/abs/math/0209021 ]
cvxopt: Python Software for Convex Optimization. [http://cvxopt.org/ ]
gensim: Topic Modeling for Humans. [http://t.cn/R4zI4yA ]
PuLP: Optimization for Python. [https://pythonhosted.org/PuLP/ ]
Demonstration of PuLP: Github: stephenhky/PyWMD. [http://t.cn/RHc6jiB ]
Implemenation of WMD: Github: stephenhky/PyWMD. [http://t.cn/RHcJLky ]
Github: stephenhky/PyWMD. [http://t.cn/RHc6F12 ]