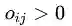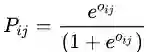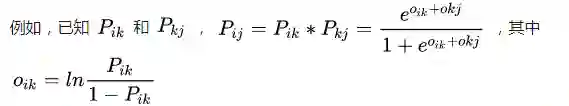通过时空模型迁移学习的无监督的跨数据集行人重新识别
CVPR2018
论文全称:Unsupervised Cross-dataset Person Re-identification by Transfer Learning of Spatial-Temporal Patterns
论文下载地址:https://arxiv.org/abs/1803.07293
代码下载地址:https://github.com/ahangchen/TFusion
摘要
大多数从事行人重识别的研究人员对具有小尺寸的单个标记数据集进行监督训练和测试,因此将这些训练模型直接部署到大规模真实世界相机网络可能由于欠拟合而导致性能差。通过使用从目标域收集的大量未标记数据来逐步优化模型是具有挑战性的。为了应对这一挑战,我们提出了一种无监督的增量学习算法TFusion,它依靠目标域中行人的时空模式的迁移学习辅助完成。具体地,该算法首先将从小标记源数据集训练的视觉分类器转移到未标记的目标数据集,以便学习行人的时空模式。其次,提出了贝叶斯融合模型,将学习的时空模式与视觉特征相结合,以实现明显改进的分类器。最后,我们提出了基于学习到排名的相互促进程序,以基于目标域中的未标记数据递增地优化分类器。进行了基于多个真实监视数据集的综合实验,结果表明,与现有的跨数据集无监督人员重新识别算法相比,我们的算法获得了显着的进步。
目标:跨数据集的行人重识别
类型:无监督学习
方法:多模态数据融合 + 迁移学习
实验效果:超越了所有无监督行人重识别方法,逼近有监督方法,在部分数据集上甚至超越有监督方法。
要解决的任务:
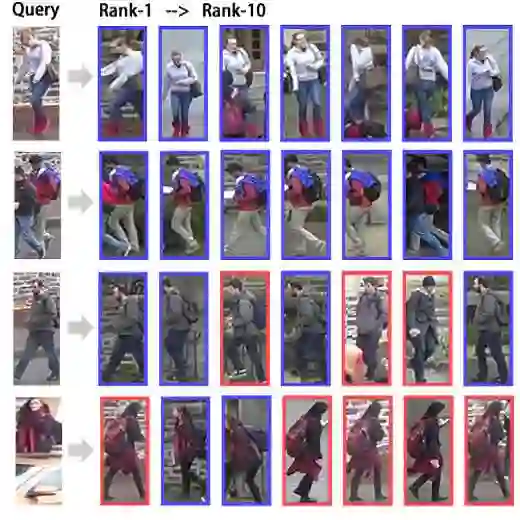
行人重识别(Person Re-identification)是一个图像检索问题,给定一组图片集(probe),对于probe中的每张图片,从候选图片集(gallery)中找到最可能属于同一个行人的图片。
行人重识别数据集是由一系列监控摄像头拍摄得到,并用检测算法将行人抠出,做行人的匹配。在这些数据集中,人脸是十分模糊的,无法作为匹配特征,而且由于多个摄像头拍摄视角不同,同个人可能被拍到正面,侧面,背面,具有不同的视觉特征,因此是一个比较难的图像匹配问题。
Related Work
有监督学习
这类方法通常需要提供行人图片和行人id标签(person1,person2等),训练模型,提取图像特征,根据两张图特征的距离大小(可以用余弦距离,欧氏距离之类的计算),为probe中的每张图和gallery中的每张图计算其相似度,根据相似度将gallery中的图片排序,排序越高越可能为同一个人。
现有的大多数人Re-ID模型都是受监督的,并且基于不变特征学习、度量学习或深度学习。然而,在大规模摄像机网络中重新id算法的实际部署中,为了支持监督学习,将大量的在线监控视频贴上标签通常是昂贵且不切实际的。
无监督学习
为了提高reid算法对大规模无标记数据集的有效性,提出了一些无监督的reid方法,从无标记数据集中学习交叉视图标识特定信息。然而,由于缺乏关于身份标签的知识,这些无监督的方法通常比有监督的学习方法产生更弱的性能。
迁移学习
迁移学习现在是深度学习领域很常用的一个套路了,在源数据集上预训练,在目标数据集上微调,从而使得源数据集上的模型能够适应目标场景。然而,目前的迁移学习大多需要标签,而无监督迁移学习效果又很差,仍然有很大提升空间。
最近,一些跨数据集传输学习算法被提出,利用在其他标记数据集中预先训练的re-id模型来提高目标数据集的性能。根据目标数据集的标签信息是否给定,这种re-id算法可以进一步分为两类:监督迁移学习和非监督迁移学习。
动机
现有的行人重识别数据集中是否包含时空信息?包含的话是否存在时空规律?
缺乏两个时空点是否属于同一行人这种标签时,如何挖掘时空信息,构建时空模型?
如何融合两个弱分类器?有监督的融合有boosting算法可以用,无监督呢?
在缺乏标签的条件下,如何进行有效的迁移学习?
对应有三个创新点
无监督的时空模型构建
基于贝叶斯推断的时空图像模型融合
基于Learning to Rank的迁移学习
接下来详细解析我们的方法。
1、时空模型
数据集中的时空规律
所谓时空模型,即一个摄像头网络中,行人在给定两个摄像头间迁移时间的分布。
我们看遍所有Reid数据集,发现有三个数据集有时空信息,Market1501, GRID, DukeMTMC4ReID,其中,DukeMTMC-ReID是2017年后半年才出来的,时间比较仓促在论文中就没有包含跟它相关的实验。Market1501是一个比较大的Person Reid数据集,GRID是一个比较小的Person Reid数据集,并且都有六个摄像头(GRID中虽然介绍了8个摄像头,实际上只有6个摄像头的数据)。
例如,Marke1501中一张图片的时空信息是写在图片名字中的:
0007_c3s3_077419_03.jpg:
0007代表person id,
c3代表是在3号摄像头拍到的,也就是空间信息,
s3代表属于第3个时间序列(GRID和DukeMTMC中没有这个序列的信息,在Market1501中,不同序列的属于不同起始时间的视频,同一序列不同摄像头的视频起始时间相近),
077419为帧号,也就是时间信息。
时空信息是非常容易保存的,只要知道图片是在什么时候,哪台摄像机上拍摄,就能够将时空信息记录并有效利用起来,希望多模态数据融合得到更多重视之后,做数据集的人能够更加重视可保存的信息吧。
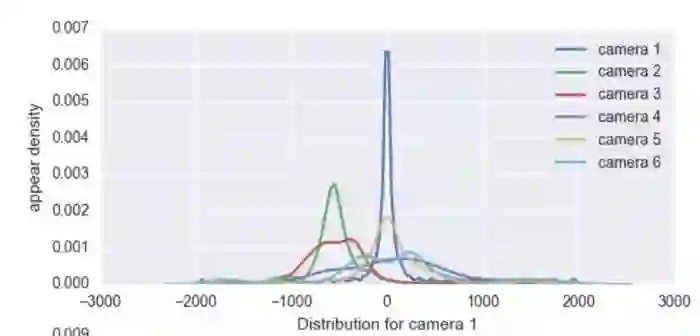
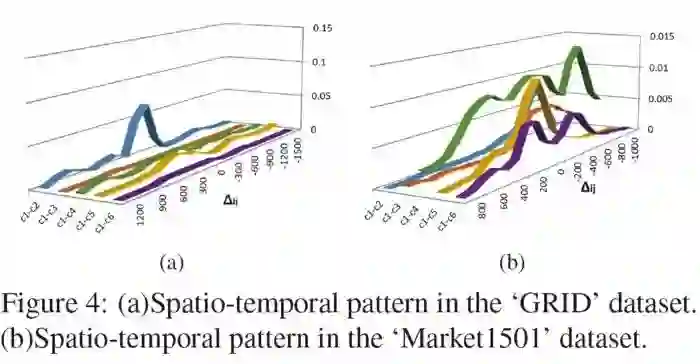
首先通过Market1501中的真实行人标签,计算训练集中所有图片对对应的时空点对对应的迁移时间,这里可视化了从摄像头1出发的行人,到达其他摄像头需要的时间的分布。
可以看到,到达不同目标摄像头的峰值位置不同,其中从摄像头1到摄像头1,意味着被单个摄像头拍到连续多帧,所以峰值集中在0附近,从摄像头1到摄像头2,峰值集中在-600附近,意味着大部分人是单向从摄像头2运动到摄像头1,等等,并且,说明这个数据集中存在显著可利用的时空规律。
无监督的时空模型构造
作者将迁移时间差命名为delta,这样说起来方便一点。
如果能够统计一个数据集中的所有delta,给定一个新的delta(两个新的图片对应的两个时空点算出来的),我们能够用极大似然估计,用在这个delta前后一定范围(比如100帧)的delta的出现频率(=目标范围delta数量/总的delta数量),作为新时间差出现的概率,也就是两个时空点是同一人产生的概率。
问题在于在目标场景上往往是没有行人标记数据。通过思考总结,是否能够根据两个时空点对应的两张图是否属于同一个人,来决定两个时空点是否属于同一个人。而两张图是否属于同一个人,其实是一个图像匹配的二分类问题,我们可以用一些视觉模型来做,但是这种视觉模型往往是需要有标签训练的,无标签的视觉模型往往比较弱。视觉模型弱没关系,我们相信跟时空模型结合就能变成一个强大的分类器。只要能够将无监督地时空模型构造出来,同时结合弱的图像分类器,效果一定超过其他无监督模型。
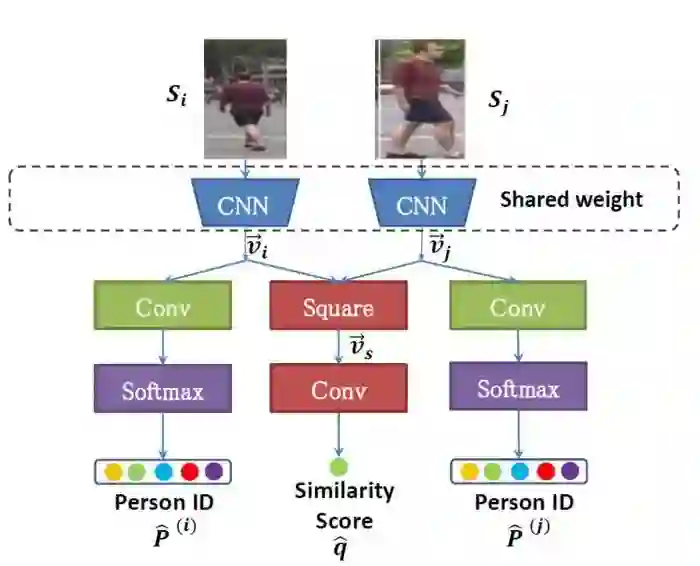
首先在其他数据集上(于是我们就可以说这是一个跨数据集的任务了)预训练一个卷积神经网络,然后用这个卷积神经网络去目标数据集上提特征,再用余弦距离算特征相似度,并将相似度排在前十的当做同一个人,用这种“同一个人”的信息+极大似然估计构造时空模型。
图像分类器上,这里用的是LiangZheng的Siamese网络,
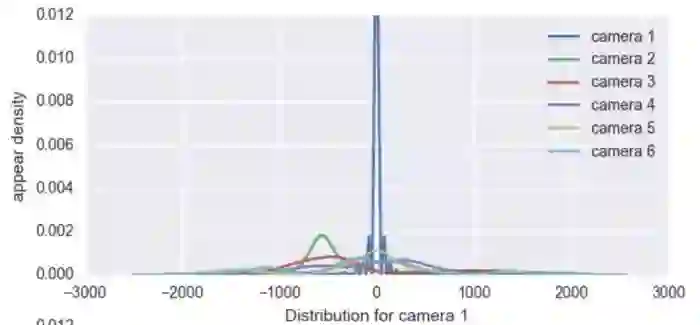
这个图像分类器是在其他数据及上预训练的,由于特征空间中数据分布不同,这个图像分类器太弱了,对于目标数据集来说,前十个排序会有许多错的样本,导致构造出来的时空模型和真实的时空模型有偏差。
可以看到,构造的模型跟真实的模型还是有些差别的,但是峰值位置还是差不多,一定程度上应该还能用,但我们还是希望构造的模型尽量接近真实模型的。
导致模型出现偏差的因素是错误的样本对,如何去掉错误样本对的影响,在没有标签的情况下,是否能够可以把错误的样本对分离出来。可以随机地选样本对,算一个随机的delta分布出来。将估算的delta分布去掉随机的delta分布,剩下的多出来的部分,就是由于正确的行人迁移产生的,就得到真实的delta分布。
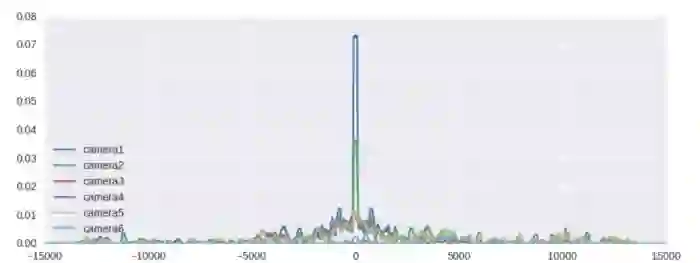
随机delta分布可视化
可以发现,确实与估计模型和真实模型不同,存在较多抖动。
这种随机的时间差分布也呈现出一定的集中趋势,其实体现的是采样的时间差分布,如,在1号摄像头采的图片大多在某个时间段,2号摄像头也大多在这个时间段采,但3号摄像头的图片大多是在其他时间段采到的。
考虑到时间差的频率图有这么多的抖动,在计算某个区域的时间差时,加上了均值滤波,并且做了一定区域的截断,包括概率极小值重置为一个最小概率值,时间差极大值重置为一个最大时间差。
如何把错误的模型从估计的模型滤掉呢?又怎么将时空模型和图像模型结合呢?
基于贝叶斯推断的模型融合
首先看时空模型和图像模型的融合, 我们有一个视觉相似度 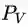
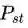
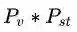
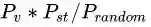
现在我们有一个弱的图像分类器,可以为两张图片提取两个视觉特征vi, vj, 有两个时空点,空间特征为两个摄像头编号ci, cj,时间特征为两张图片拍摄的时间差∆ij,假定两张图对应的person id分别为Pi, Pj,那么目标就是求:在给定这些特征的条件下,两张图属于同一个人的概率。
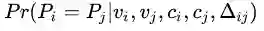
由条件概率公式 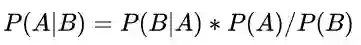
由时空分布和图像分布的独立性假设(长得像的人运动规律不一定像),我们可以拆解第一项,得到
其中
先交换顺序(乘法交换律)
由条件概率公式 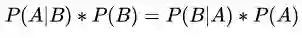
可以看到
可理解为两张图从视觉特征相似度上判定为同一人的概率
就是两个时空点是同一个人移动产生的概率
再次利用时空分布和图像分布的独立性假设,拆解分母
也就是= 视觉相似度*同一人产生这种移动的概率/任意两个时空点组成这种移动的概率这也就是论文公式(7),也就是我们一开始的猜想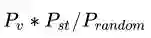
看着好像很接近我们手头掌握的资源了,但是我们并不知道理想的两张图的视觉相似度 ,只有我们的图像分类器判定的两张图的视觉相似度 。我们并不能计算同一人产生这种移动的真实概率 ,我们只有依据视觉分类器估算的时空概率 。我们倒是确实有数据集中任意两个时空点产生这种移动的概率P(ci,cj,∆ij)。
看到这里其实就大致理解我们的融合原理了,实际上我们大部分实验也是用的这个近似公式算的。
但这个近似能不能做呢?我们来做一下误差分析(大量推导,不感兴趣可以跳到接下来出现的第二张图,不影响后面的理解,只是分析一波会更加严谨)。
实际上,误差是由图像分类器引入的,假设图像分类器判定两张图是同一个人的错判率为Ep,图像分类器判定两张图不是同一人的错判率为En,
推导,Pr(ci,cj,∆ij|Pi=Pj) 和Pr(ci,cj,∆ij|Si=Sj) 的关系(这个没法像视觉相似度那样直接推导,因为因果关系不同)
同样可以得到
其中有个新概念Pr(ci,cj,∆ij|Si≠Sj) ,意味着图像分类器认为不是同一个人的时候,这种时空点出现的概率,实现上也不难,统计视觉相似度top10以后的点对应的时间差,作为反时空概率模型即可。
我们把两个近似(公式5和公式8)代进公式7,
可以得到
以上四项都是可以从无标签目标数据集中结合图像分类器求解到的,并且,当 
到这里,你是不是以为我们就可以用公式9算融合评分了?非也,公式9中,还有个问题: Ep,En 是未知的!
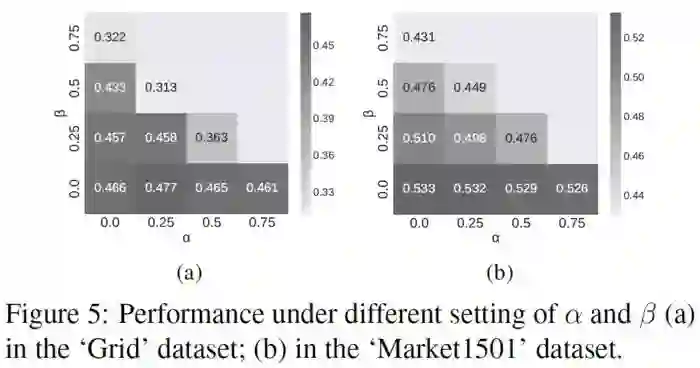
如果想要正儿八经地算 , Ep,En 要求目标数据集有标签,然后我们用图像分类器先算一遍,数数哪些算错了,才能把 Ep,En 算出来。因此我们用两个常数α和β分别替代 ,Ep,En 整个模型的近似就都集中在了这两个常数上。
在论文Table1,2,3,4,Fig6相关的实验中,α=β=0,并且,在Fig5中,我们设置了其他常数来检查模型对于这种近似的敏感性.
可以看到,虽然α和β较大时,准确率会有所下降,但是仍然能保持一定的水准,当你看到纯图像分类器的准确率之后,还会发现融合模型的准确率一直高于纯图像分类器。
你可能注意到了,图中α+β都是小于1的,这是因为,只有当Ep+En<1且α+β<1时,融合模型的Ep+En才会小于图像模型的Ep+En,说人话就是,只有图像模型不是特别糟糕,且近似的参数也比较正常的时候,融合模型才会比单个的图像模型要准,融合才有意义。这个定理的具体的证明放到论文附录里了,有兴趣的可以邮件私信我拿附录去看,这里摆出来就太多了。
于是我们得到了一个由条件概率推断支撑的多模态数据融合方法,称为贝叶斯融合
看一眼融合得到的时空分布图:
再从数据上看一眼融合的模型
可以看到,
跨数据集直接迁移效果确实很差
融合之后的准确率Rank1准确率变成2-4倍
说明这种融合方式是确实行之有效的。
基于Learning to Rank的迁移学习
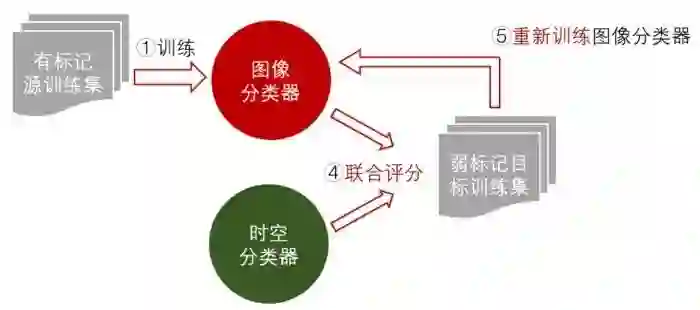
前面讲到图像分类器太弱了,虽然融合后效果挺好的(这个时候我们其实想着要不就这样投个NIPS算了),但是如果能提升图像分类器,融合的效果理论上会更好。而现在我们有了一个强大的融合分类器,我们能不能用这个融合分类器为目标数据集的图片打标签,反过来训练图像分类器呢?
一个常用的无监督学习套路就是,根据融合评分的高低,将图片对分为正样本对和负样本对(打伪标签),然后喂给图像分类器学习。
我们也尝试了这种做法,但是发现,数据集中负样本远远多于正样本,融合分类器分对的负样本是挺多的,但是分对的正样本超级少,分错的正样本很多,错样本太多,训练出来效果极差,用上一些hard ming的技巧也不行。
于是我们思考,
我们无法提供正确的01标签,分类器就只能学到许多错的01标签
我们是否可以提供一些软标签,让分类器去学习回归两个样本之间的评分,而不是直接学习二分类的标签?
这是一个图像检索问题,我们能不能用信息检索中的一些学习方法来完成这个任务?
于是自然而然地想到了Learning to Rank
Ranking
问题定义:给定一个对象,寻找与其最相关的结果,按相关程度排序
常用方法:
Point-wise:每一个结果算一个绝对得分,然后按得分排序
Pair-wise:每两个结果算一下谁的得分高,然后按这个相对得分排序
List-wise:枚举所有排列情况,计算综合得分最高的一种作为排序结果
综合得分往往需要许多复杂的条件来计算,不一定适用于我们的场景,所以排除List-wise,Point-wise和Pair-wise都可以采用,得分可以直接用融合评分表示,Pair-wise可以用一组正序样本,一组逆序样本,计算两个得分,算相对得分来学习,有点Triplet loss的意味,于是在实验中采用了Pair-wise方法。
Pair-wise Ranking
给定样本Xi,其排序得分为 Oi,
给定样本Xj,其排序得分为Oj,
定义
如果
说明Xi的排名高于Xj
将这个排名概率化,定义
为xi排名高于xj的概率。
对于任何一个长度为n的排列,只要知道n-1个相邻item的概率
,就可以推断出来任何两个item的排序概率
RankNet: Pair-wise Learning to Rank
RankNet是Pair-wise Learning to Rank的一种方法,用一个神经网络去学习输入的两个样本(还有一个query样本)与其排序概率(上面定义的)的映射关系。
具体到我们这个问题里
给定查询图片A,给定待匹配图片B和C
用神经网络预测AB之间的相似度Sab为B的绝对排序得分,计算AC之间的相似度Sac为C的绝对排序得分
Transfer Learning to rank
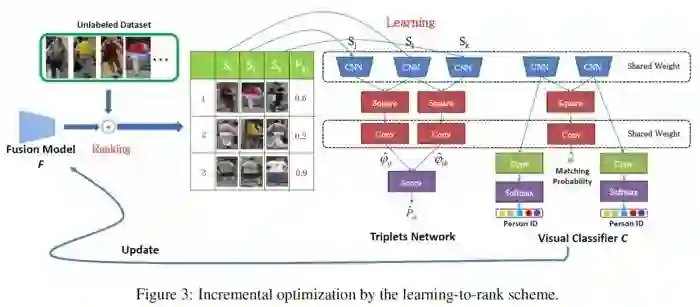
整个Learning to rank过程如图
我们用融合分类器为目标数据集中的图片对评分,构造三元组输入RankNet,其中Si是查询图,Sj是在与Si融合相似度top1 - top25中抽取的图片,Sk是在与Si融合相似度top25 - top50中抽取的图片,喂给RankNet学习,使得resnet52部分卷积层能充分学习到目标场景上的视觉特征。
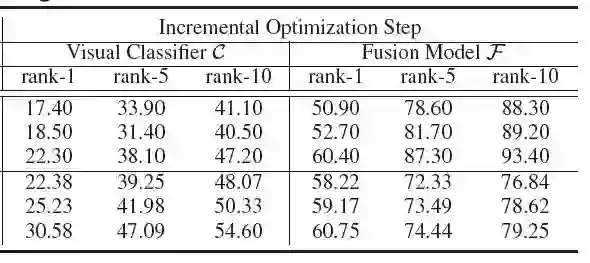
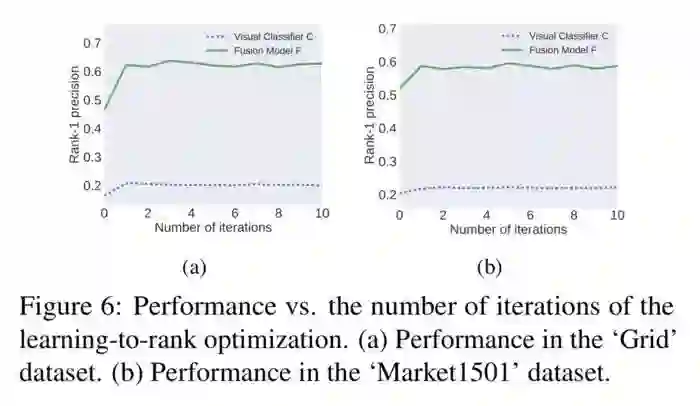
Learning to Rank效果
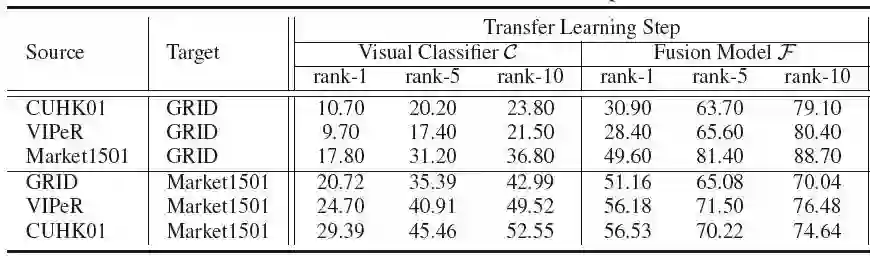
对比Learning to Rank前的效果,准确率都提升了,GRID数据集上提升尤为明显。
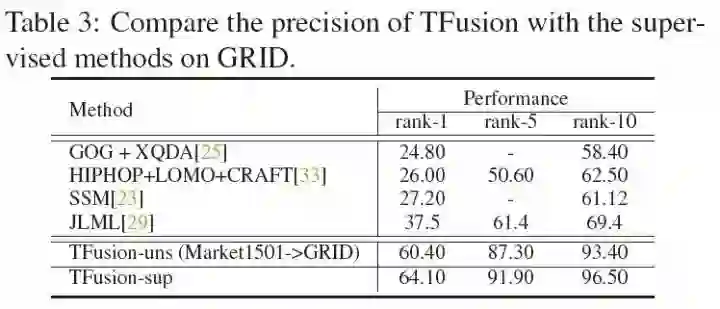
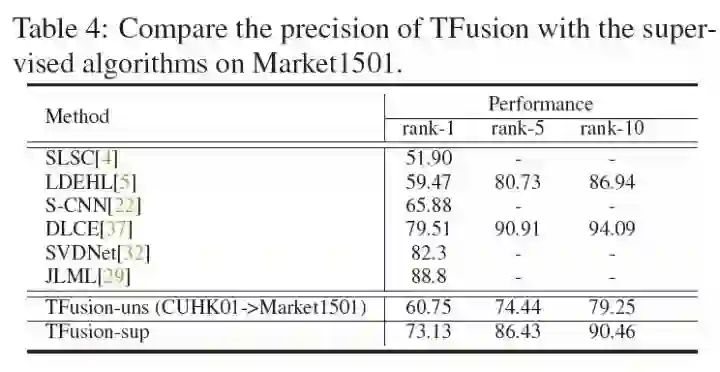
对比SOA有监督方法
一方面,我们将上面的跨数据集无监督算法应用在GRID和Market1501两个数据集上,与当前最好的方法进行对比,另一方面,我们还测试了有监督版本的效果,有监督即源数据集与目标数据集一致,如GRID预训练->GRID融合时空,效果如下:
GRID
由于在这个数据集上时空规律十分明显(正确时间差都集中在一个很小的范围内),可以过滤掉大量错误分类结果,所以准确率甚至碾压了全部有监督方法。
Market1501
在Market1501这个数据集上,无监督的方法逼近2016年的有监督方法(我们的图像分类器只是一个ResNet52),有监督的方法超越2016年的有监督方法,虽然比不上2017年的有监督方法,但是如果结合其他更好的图像分类器,应该能有更好的效果。
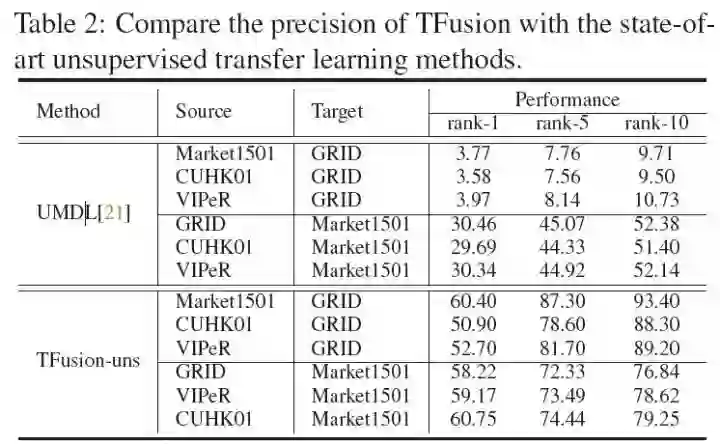
对比SOA无监督方法
我们向UMDL的作者要到了代码,并复现了如下几组跨数据集迁移实验
其中,UMDL迁移到Market1501的结果与悉尼科技大学hehefan与LiangZheng复现出来的效果差不多,所以我们的复现是靠谱的。
可以看到,无监督的TFusion全面碾压UMDL。
更多详细实验结果可以到论文中细看。
多次迭代迁移学习
回顾一下整个架构,我们用图像分类器估算时空模型,得到融合模型,用融合模型反过来提升图像分类器模型,图像分类器又能继续增强融合模型,形成一个闭环,理论上这个闭环循环多次,能让图像分类器无限逼近融合分类器,从而得到一个目标场景中也很强大的图像分类器,因此我们做了多次迭代的尝试:
在从目前的实验效果看,第一次迁移学习提升比较大,后面提升就比较小了,这个现象往好了说可以是收敛快,但往坏了说,虽然图像分类器得到了提升,但是没有出现图像分类器提升大于融合分类器的现象,所以这里边应该还有东西可挖。
读文章是看到作者的GITHUB,并了解了其在创新时一步一步的思想。
感谢https://github.com/ahangchen 的博客以及公开代码。

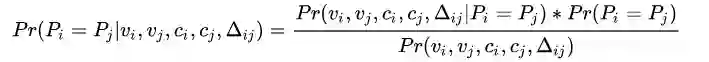
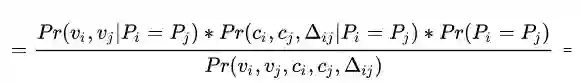
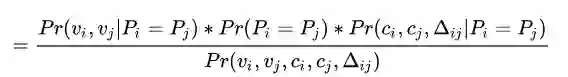
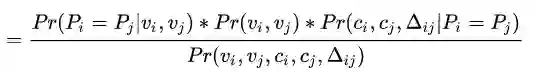
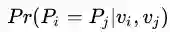 可理解为两张图从视觉特征相似度上判定为同一人的概率
可理解为两张图从视觉特征相似度上判定为同一人的概率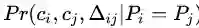 就是两个时空点是同一个人移动产生的概率
就是两个时空点是同一个人移动产生的概率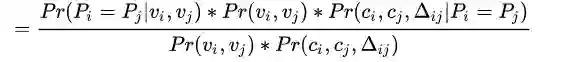
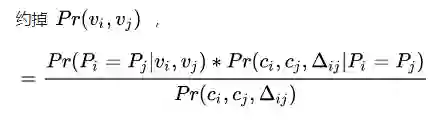
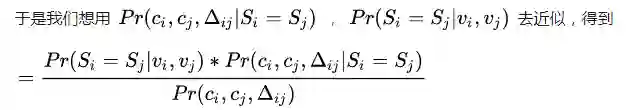

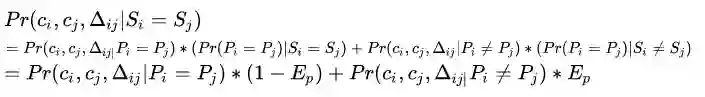
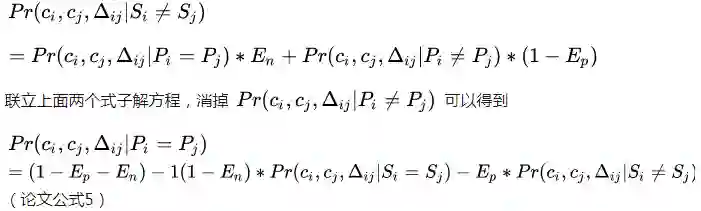

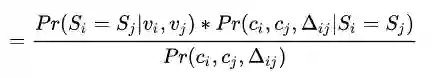
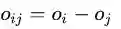 如果
如果