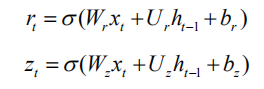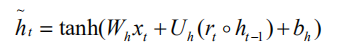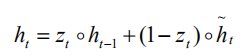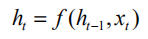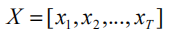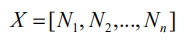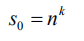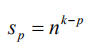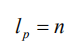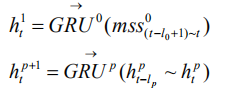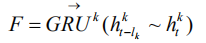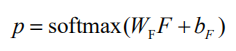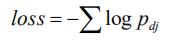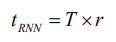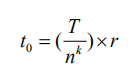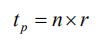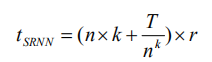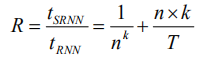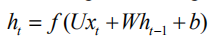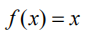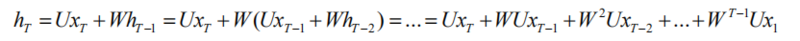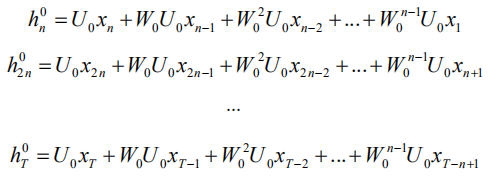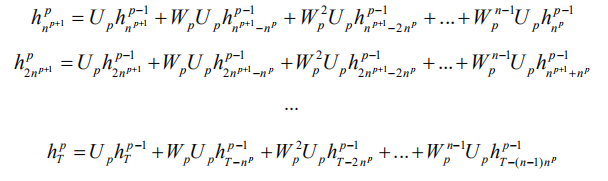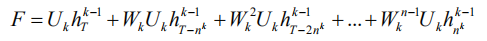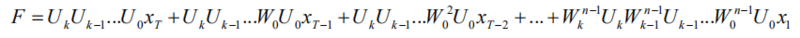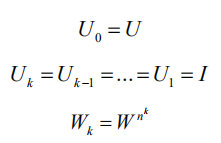比RNN快136倍！上交大提出SRNN引发热议（代码已开源）

2018 年 8 月 19 日 AI前线

作者 | Zeping Yu，Gongshen Liu

编译 | 马卓奇

编辑 | Natalie

AI 前线导读： 循环神经网络（RNN）在许多 NLP（神经语言处理）任务中取得了巨大的成功。然而，由于循环单元结构很难并行化计算，因此训练 RNN 往往需要花费大量的时间。上海交通大学研究人员提出了切片循环神经网络（SRNN），可以通过将序列分割成多个子序列来实现并行化计算。SRNN 具有通过多层网络和极少的额外参数来获得高层次信息的能力。不需要改变循环单元，SRNN 的速度便可以达到标准 RNN 的 136 倍，而且训练更长的序列时，SRNN 的速度还能更快。研究人员在六个大规模情感分析数据集上进行了实验，实验结果表明 SRNN 的性能均优于标准的 RNN。本文已发表在顶级计算机语言学大会 COLING 2018，且所涉及的项目代码已经在 Github 上开源。SRNN 究竟有多好，AI 前线第 45 篇论文导读将带你一探究竟！

更多优质内容请关注微信公众号“AI 前线”（ID：ai-front）

一、介绍

RNN 能够获取输入序列的顺序信息。两个最常用的循环单元是长短时记忆（LSTM）和门控循环单元（GRU），二者均能在隐状态存储之前的记忆，并使用门机制来决定有多少之前的记忆需要和当前输出结合。然而由于循环结构，RNN 不能并行计算。因此训练 RNN 需要花费大量时间，从而限制了 RNN 在科研和工业的发展。

一些学者通过改进循环单元来提升 RNN 的速度，也取得了较好的成果。但是这种方法虽然提升了 RNN 的速度，整体序列的循环结构并没有改变。我们依然需要等待前一步的输出，所以阻碍 RNN 速度提升的瓶颈依然存在。在这篇文章中，我们将介绍切片循环神经网络（SRNN），SRNN 的速度显著快于标准的 RNN，而且不需要改变循环单元。当我们使用线性激活函数时，标准 RNN 即为一种特殊的 SRNN，并且 SRNN 具有提取序列高级信息的能力。

为了方便对比，我们选用 GRU 作为循环单元。其他循环单元也可以用在 SRNN 的结构中，因为我们改进的是 RNN 的整体结构，而不是循环单元。

二、模型结构

门控循环单元 GRU

GRU 由 reset gate r 和 update gate z 组成。Reset gate 决定有多少之前的记忆需要和新的输入结合，而 update gate 决定多少之前的记忆被保留下来。

其中 x 是输入，h 是隐状态。

候选隐状态 ht 由 reset gate 控制。当 reset gate 为 0 时，之前的记忆就被忽略了。

当 update gate 为 1 时，隐状态将之前的记忆拷贝给当前时刻，并且忽略当前输入。

标准 RNN 结构

标准 RNN 结构如图 1 所示，A 代表循环单元。

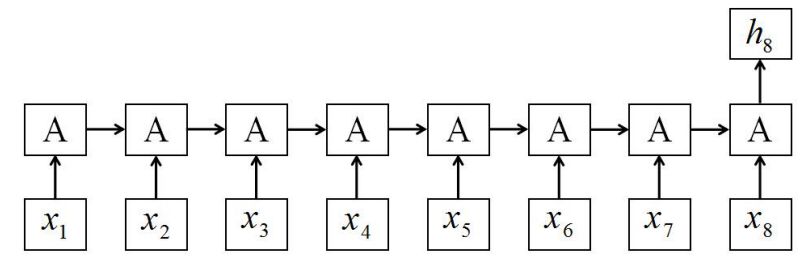
图 1 标准 RNN 结构，每一步都需要等待前一步循环单元计算输出。

输入序列 X 的长度为 T，假设 T=8。标准 RNN 使用最后的隐状态 h8 作为全部序列的表示，然后增加一个 softmax 分类器来预测类标。在每一步，我们都需要等待网络计算前一步的输出：

这一标准 RNN 结构由于每两个相邻神经元的连接，从而引起了速度瓶颈：输入序列越长，需要的时间越长。

切片循环神经网络（SRNN）

我们建立了一种新的 RNN 结构：切片循环神经网络（SRNN），如图 2 所示。

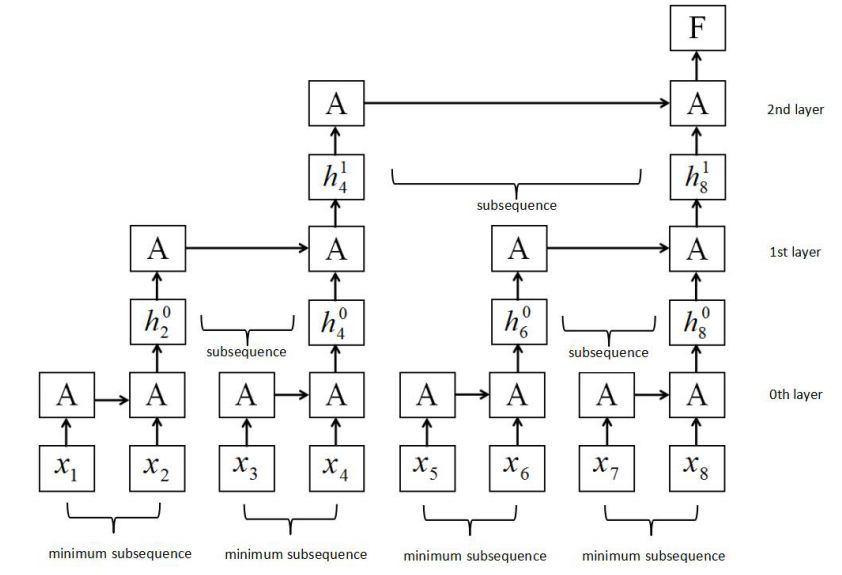
图 2 SRNN 结构。

SRNN 将输入序列划分成几个等长的最小序列，循环单元在每层的小序列上同时工作，然后信息可以通过多个网络层进行传递。

假设输入序列 X 的长度为 T，输入序列为：

其中 x 是每一步的输入，可以有多个维度。然后我们将 X 划分成 n 个等长的子序列，每一个子序列 N 的长度为：t=T/n。

因此序列 X 则可以表示为：

每一个子序列为：

类似的，我们再将每个子序列 N 划分成 n 个等长的序列，然后重复这样的划分操作 k 次，直到最底层的最小子序列长度合适（图 2 中的第 0 层），然后通过这 k 次分割，就可以得到 k+1 层网络。第 0 层的最小子序列长度为：

第 0 层的最小子序列数量为：

由于 p 层的每个输入序列都被划分为 n 块，第 p 层的子序列数量为：

第 p 层的子序列长度为：

以图 2 为例，序列长度为 T=8，切片次数 k=2，每一层的切片数 n=2。通过两次分割操作，我们在第 0 层得到了 4 个最小子序列，每个最小子序列的长度为 2。如果序列或子序列的长度不能被 n 整除，我们就利用 padding 的方法或者在每一层选择不同的切片数。

SRNN 与标准 RNN 的不同在于，SRNN 将输入序列切割成许多最小子序列，并且在每个子序列上应用循环单元。这样一来，子序列就可以并行计算。在第 0 层，循环单元通过连接结构在每个最小子序列上进行操作。随后，我们获取每个最小子序列的最后的隐状态作为第 1 层的输入。以此类推，在 p-1 层每个子序列的最后的隐状态都作为第 p 层的输入子序列，然后计算第 p 层子序列最后的隐状态：

我们在每一层均重复该操作，直到我们获得顶层（第 k 层）的隐状态 F：

分类问题

与标准 RNN 类似，我们将 softmax 层加在最终的隐状态 F 后面对类标进行分类：

损失函数为负对数似然函数：

速度优势

SRNN 之所以能够并行计算是因为它改进了传统的连接结构。在 SRNN 中，不是每一个输入都与其之前的时刻相关联，但是整个序列通过切片的方式连接起来。SRNN 依然可以通过每个子序列的循环单元获取序列顺序，然后通过多层网络传递信息。假设每个循环单元需要花费的时间为 r，则标准 RNN 需要花费的时间为：

T 为序列长度。而在 SRNN 中，每个最小子序列可以并行计算，所以在第 0 层花费的时间为：

以此类推，在第 p 层花费的时间为：

因此 SRNN 花费的总时间为：

我们可以计算出 SRNN 的速度优势：

R 是 SRNN 比标准 RNN 快的倍数。我们可以选择不同的 n 和 k 来得到不同的速度优势。

SRNN 与标准 RNN 的关系

在标准 RNN 结构中，每一步都与输入和前一步相关：

其中 x 表示输入，h 表示隐状态。函数 f 可以是非线性激活函数，例如 sigmoid，或者线性激活函数例如 ReLU。为了简化问题，我们讨论使用线性函数的情况：

我们将偏置 b 和 h0 设为 0。对于标准 RNN，最后的隐状态可以通过如下计算得到：

假设我们构建 SRNN（n，k），即切片 k 次，切片数量为 n。SRNN 有 k+1 层，每一层的子序列长度为 n。我们可以计算第 0 层每个最小子序列的最后输出隐状态：

类似的，我们将 p-1 层得到的隐状态作为第 p 层的输入，然后计算第 p 层的隐状态：

从第 0 层到第 k 层重复该操作，最后可以得到第 k 层的最终隐状态 F：

当我们把之前层的隐状态计算公式代入上式，可以得到：

对比该式和标准 RNN 的计算式，我们可以发现当满足如下条件时：

这两个公式可以得到相同的结果。其中 I 为单位矩阵，U 和 W 是网络参数。这意味着当函数 f 为线性函数，并且满足上述条件时，SRNN 的输出与标准 RNN 的输出相同，所以标准 RNN 是 SRNN 的一种特殊情况。因此，当不同层的参数不同时，SRNN 比标准 RNN 能够从输入序列中获取更多的信息。

三、实验

数据集

我们在 6 个大型情感分析数据集上对 SRNN 进行测试。表 1 给出了这些数据集的信息。每个数据集的 80% 用于训练，10% 用于验证，10% 用于测试。

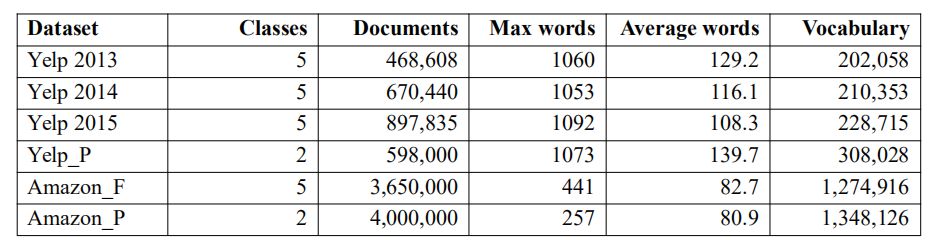
表 1 数据集信息

Yelp 点评：Yelp 点评数据集来自 Yelp 数据集挑战赛，有 5 个情感标签。这个数据集包含 4736892 个文档，我们提取了三个子集，Yelp2013，2014 和 2015，分别包含 468608、670440 和 897835 个文档。Yelp_P 是极性数据集，仅包含两类情感类标，一共 598000 个文档。

Amazon 点评：Amazon 点评数据集包含对 2441053 个产品的 34686770 条点评，来自 6643669 个用户。每条评论都有一个标题、一条内容和一个情感类标，我们将标题和内容结合成一个文档。这个数据集也被分为一个完整数据集，具有 3650000 个文档，和一个极性数据集，具有 4000000 个文档。

实验基线

我们主要对比 SRNN 和标准 RNN 结构，用 GRU 作为循环单元。我们用最后输出的隐状态作为文档的表示，在后面接入 softmax 层来预测类标。为了将 SRNN 和卷积结构进行对比，我们也构造了空洞因果卷积层作为实验基线。

训练

我们使用 Keras 自带的序列预处理工具，使所有序列的长度均为 T。短于 T 的序列在末端补 0，长于 T 的序列则从末端裁剪。Yelp 数据集的 T 设为 512，Amazon 数据集的 T 设为 256。对于每个数据集，我们用出现频率最高的 30000 个词作为词典。用预训练的 GloVe 来初始化词嵌入。

GRU 的循环单元激活函数为 sigmoid 函数，每一层之后的激活函数为线性函数。

实验结果与分析

表 2 给出了每个数据集上的实验结果。我们选用了不同的 n 和 k 值，得到了不同的 SRNN。例如 SRNN（16，1）表示 n=16，k=1，即当序列长度 T=512 时，最小子序列长度为 32。

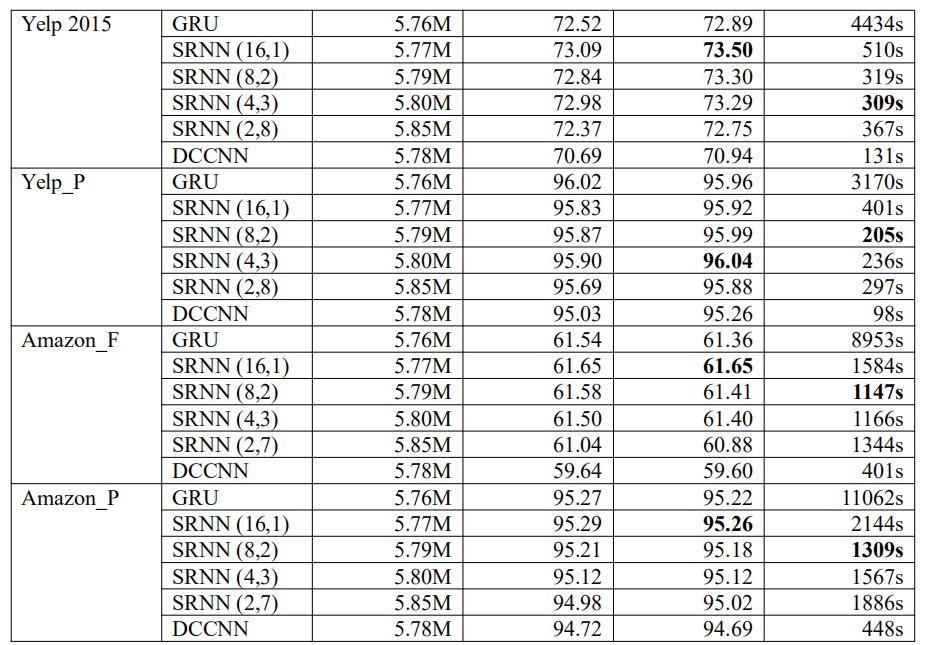
表 2 模型在验证集和测试集上的准确率和训练时间

实验结果表明 SRNN 的表现更好，并且比标准 RNN 具有更高的速度，而且参数更少。在不同数据集上，不同结构的 SRNN 分别取得了不同的表现。通过对比在 Yelp 数据集上测试的 SRNN（2，8）和在 Amazon 数据集上测试的 SRNN（2，7），我们发现即使他们没有获得最好的表现，也并没有损失太多准确率。这意味着 SRNN 能够将信息在多层网络之间传递，正因为如此，SRNN 在训练很长的序列时可取得显著成效。当 n=2 时，SRNN 与 DCCNN 具有相同的层数，但是其准确率远远高于 DCCNN。这也说明 SRNN 的循环结构要优于空洞因果卷积结构。

当 n 和 k 的值较大时，SRNN 的速度可以更快。我们在 5120 个文档上训练了模型，训练时间如表 3 所示。

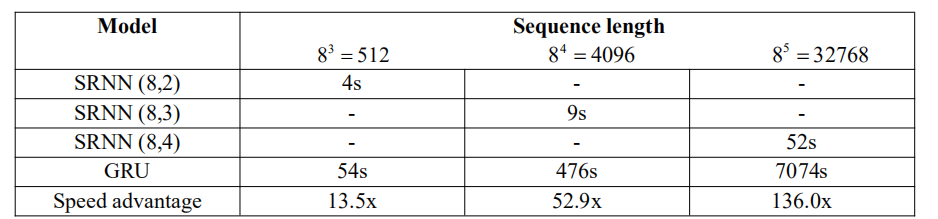
表 3 在不同序列长度上的训练时间和速度优势

当序列长度为 32768 时，SRNN 只需要 52 秒，而标准 RNN 需要将近 2 个小时，SRNN 比标准 RNN 快 136 倍。并且序列长度越长，SRNN 的速度优势就越明显。因此 SRNN 可以在例如语音识别、字符级别文本分类和语言建模等长序列任务上获得更快的速度。

为什么选择 SRNN

这一部分我们将讨论 SRNN 的优势和重要性。随着 RNN 在 NLP 任务中的成功应用，许多研究提出通过改进 RNN 循环单元的结构来提升 RNN 的速度。但是 RNN 的连接结构才是限制 RNN 速度提升的瓶颈。SRNN 通过切片结构提升了传统的连接结构，从而实现了 RNN 的并行计算。实验结果显示 SRNN 比标准 RNN 取得了更好的表现。

我们将原因归纳为以下三点：

（1）当我们使用标准 RNN 连接结构时，循环单元很重要，但是当序列很长时，它们不能存储所有的重要信息。而 SRNN 将长序列分割成许多短的子序列，并且提取了短序列中的重要信息。SRNN 能够将重要信息在多层结构中传递。

（2）SRNN 能够从序列中获取高级信息，而不仅仅是单词级别的信息。以 SRNN（8，2）为例，第 0 层获取的是从词嵌入中得到的语句级别的信息，第 1 层可以获得段落级别的信息，而第 2 层可以产生最终的文档级别的信息。而标准 RNN 只能获得单词级别的信息。

（3）从处理序列的角度来看，SRNN 更接近人类大脑的机制。例如，如果给我们一篇文章，并且向我们提出一些相关问题，我们一般不需要阅读整篇文章来得到正确答案。我们会定位到具体信息的段落，然后找到能够回答问题的语句。SRNN 也可以通过多层网络结构做到这一点。

除了准确率的提升，SRNN 最重要的优势在于它可以并行计算，从而获得更高的速度。实验结果和理论推导都证明 SRNN 的速度可以达到标准 RNN 的数倍。并且 SRNN 在越长的序列长可以得到更快的速度。随着网络的发展，每天都在产生大量的数据，而 SRNN 为我们处理这些数据提供了新方法。

四、未来研究方向

SRNN 在文本分类问题中已经得到了成功应用，在未来，我们希望将其推广至更多 NLP 问题，例如回答问题、总结文本和机器翻译。在 Seq2Seq 模型中，SRNN 可以用作编码器，而解码器可以通过反 SRNN 结构来改进。我们希望 SRNN 可以用于长序列任务，例如语言模型、音乐生成和语音生成。未来我们将探索更多的 SRNN 变体，例如加入双向结构和注意力机制。

查看论文原文：

https://arxiv.org/ftp/arxiv/papers/1807/1807.02291.pdf

项目开源代码：

https://github.com/zepingyu0512/srnn