一元线性回归预测：销售收入与广告支出实战

会员服务 ·

一元线性回归预测：销售收入与广告支出实战

2019 年 1 月 2 日 R语言中文社区

2019

万事胜意

作者：herain R语言中文社区专栏作者

知乎ID：https://www.zhihu.com/people/herain-14

前言

数据挖掘的学习中，一元线性回归，通过现实生活中的企业销售和广告支出这两者之间的联系，进行线性回归模型的学习和形成商业二维变量分析的方法。

前提：一元回归的建模思路大致如下：

第一步：确定因变量与自变量之间的关系
第二步：建立线性关系模型，并对模型进行估计和检验
第三步：利用回归方程进行预测
第四步：对回归模型进行诊断

1 确定因变量与自变量之间的关系

1.1 确定变量之间的关系

数据：企业的销售收入与广告支出的二维表：（example9_1数据框）

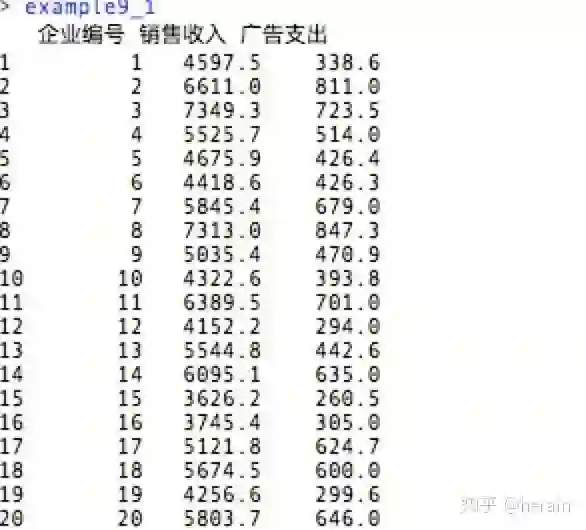
1.2 相关关系的描述

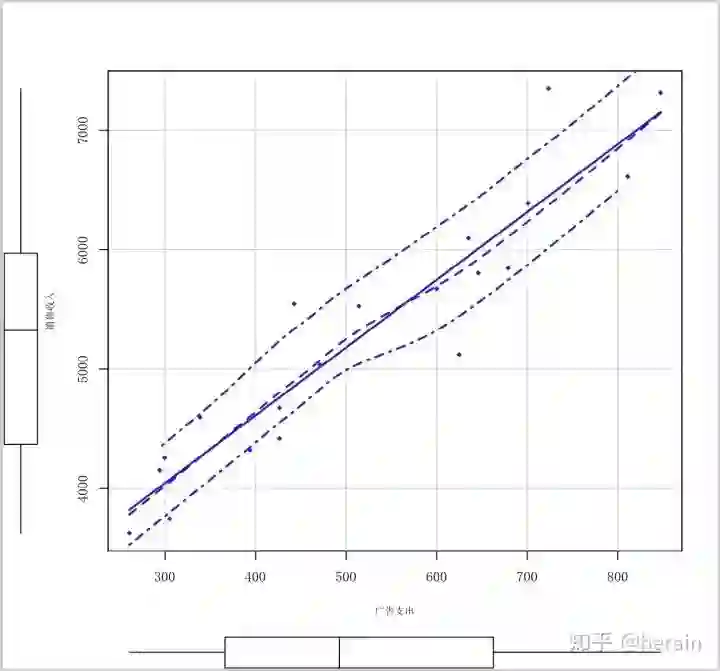
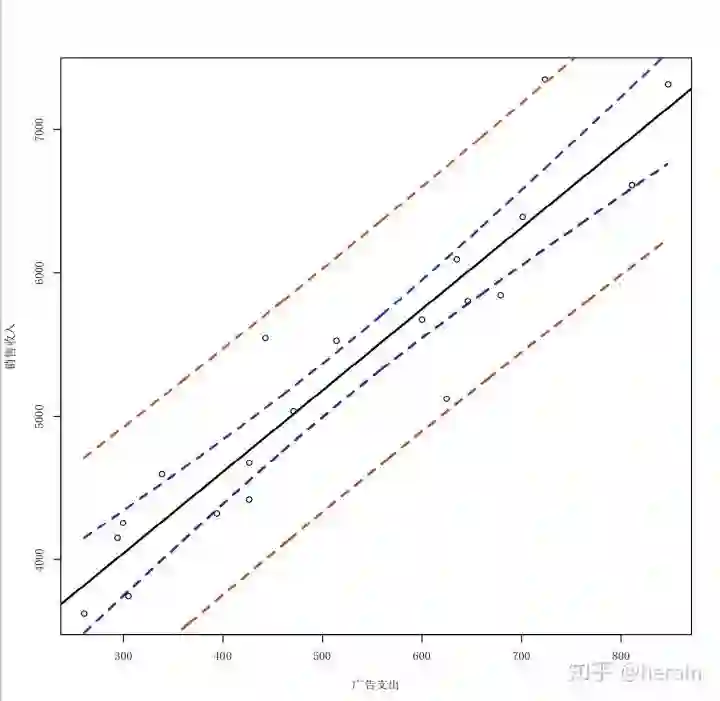
对数据example9_1用scatterplot图表化，一目了然变量之间的关系(初步结论变量之间存在正向的线性关系)：

library('car')
scatterplot(销售收入~广告支出, data=example9_1,spread=F,lty.smooth=1, pch=18, xlab="广告支出",ylab="销售收入",cex.lab=0.7, family = 'SimSun')

1.3 关系强度的度量

相关系数两变量之间线性关系强度的统计量r（也叫做pearson 相关系数，-1<=r<=1）, 具体公式请参考资料。

> cor(example9_1[,2], example9_1[,3])
[1] 0.937114

相关系数的检验，用t分布检验：

第一步：提出假设：

原假设：两个变量的线性关系不显著

备择假设：两个变量的线性关系显著

第二步：计算统计变量t:

install.packages("psych",repos="The Comprehensive R Archive Network") 
library(psych)

cor.test(example9_1[,2], example9_1[,3])

    Pearson's product-moment correlation

data:  example9_1[, 2] and example9_1[, 3]
t = 11.391, df = 18, p-value = 1.161e-09
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 0.8450142 0.9752189
sample estimates:
     cor 
0.937114

第三步：进行决策：统计量P值小于0.05，拒绝原假设，得出两个变量的线性关系显著

2 建立线性关系模型，并进行估计与检验

2.1 建立回归模型：

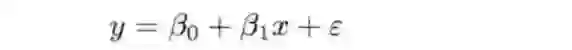
2.2 参数的最小二乘法估计：

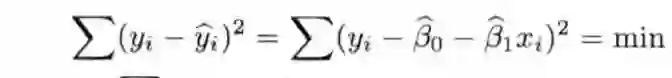
一元线性回归（主要统计量，参数估计和检验值）
md <- lm(销售收入~广告支出, data= example9_1)
summary(md)
Call:
lm(formula = 销售收入 ~ 广告支出, data = example9_1)

Residuals:
    Min      1Q  Median      3Q     Max 
-766.30 -273.85  -26.79  174.73  900.66 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) 2343.8916   274.4825   8.539 9.56e-08 ***
广告支出       5.6735     0.4981  11.391 1.16e-09 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 394 on 18 degrees of freedom
Multiple R-squared:  0.8782,    Adjusted R-squared:  0.8714 
F-statistic: 129.8 on 1 and 18 DF,  p-value: 1.161e-09

回归系数的置信区间：
> confint(md,level=0.95)
                  2.5 %      97.5 %
(Intercept) 1767.225152 2920.558006
广告支出       4.627092    6.719825

方差分析：
anova(md)
Analysis of Variance Table

Response: 销售收入
          Df   Sum Sq  Mean Sq F value    Pr(>F)    
广告支出   1 20139304 20139304  129.76 1.161e-09 ***
Residuals 18  2793629   155202                      
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

由R计算可知，销售收入与广告支出的估计方程为：

y = 2343.8916 + 5.6735 * 广告支出（可以用于预测）

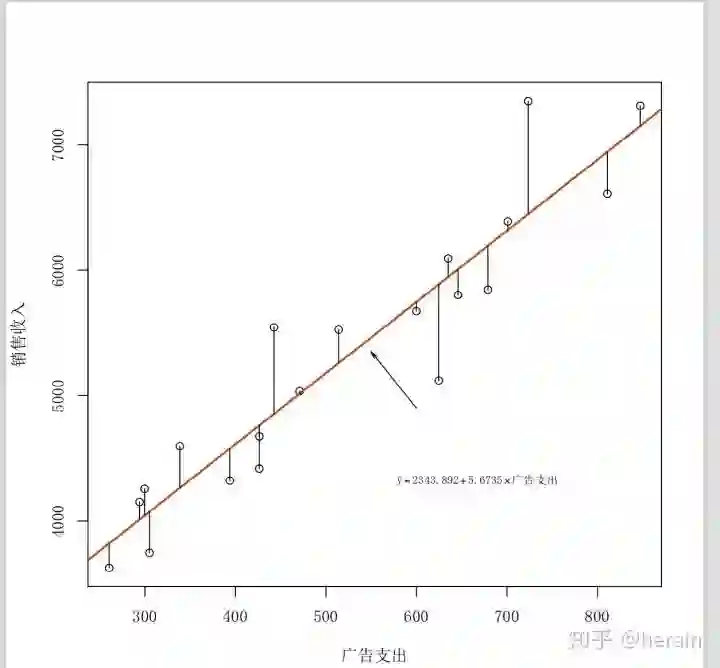
2.3 模型的拟合优度（回归直线与各观测点的接近程度），统计量是判定系数（可决系数）

2.3.1 决定系数

md <- lm(销售收入~广告支出, data= example9_1)
plot(销售收入~广告支出, data= example9_1, family = 'SimSun')
text(销售收入~广告支出,labels=企业编号，cex=0.6,adj=c(-0.6,0.25),col=4,family = 'SimSun')
abline(md, col=2,lwd=2)
n = nrow(example9_1)
for(i in 1:n){segments(example9_1[i,3], example9_1[i,2], example9_1[i,3],md$fitted[i])}
mtext(expression(hat(y)== 2343.8916+ 5.6735%*%广告支出),cex=0.7,side=1,line=-6,adj=0.75, family = 'SimSun')
arrows(600,4900,550,5350,code=2,angle=15,length=0.08)

（点击放大）

2.3.2 残差标准误（残差平方和的均方根）公式具体参考教材

2.4 模型的显著性检验（F分布检验）

2.4.1 线性关系检验

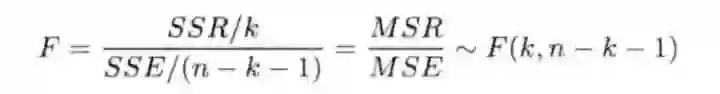
省略检验步骤，参考方差分析：F = 129.76, P =1.161e-09 线性关系显著

2.4.2 回归系数的检验和推测

省略检验步骤：参数的置信区间如下

confint(md,level=0.95)                   
             2.5 %      97.5 % 
(Intercept) 1767.225152 2920.558006 
广告支出       4.627092    6.719825

3 利用回归方程进行预测

基于多点的点估计，求出区间估计（均值的区间估计，个别值的预测区间）

计算公式请参考教材

均值的区间估计：
md <- lm(销售收入~广告支出, data= example9_1)
> x0 <- example9_1$广告支出
> pre_fit<-predict(md)
> con_int<-predict(md, data.frame(广告支出=x0), interval="confidence", level=0.95)
> pre_int<-predict(md, data.frame(广告支出=x0), interval="prediction", level=0.95)
> pre<-data.frame(y=example9_1$销售收入, pre_fit, lci = con_int[,2], uci=con_int[,3], lpi=pre_int[,2], upi=pre_int[,3])
> pre
       y  pre_fit      lci      uci      lpi      upi
1  4597.5 4264.925 3998.348 4531.501 3395.383 5134.467
2  6611.0 6945.066 6590.492 7299.641 6044.643 7845.490
3  7349.3 6448.639 6168.060 6729.217 5574.703 7322.575
4  5525.7 5260.049 5074.789 5445.310 4411.897 6108.201
5  4675.9 4763.054 4552.697 4973.412 3909.069 5617.039
6  4418.6 4762.487 4552.080 4972.894 3908.490 5616.484
7  5845.4 6196.170 5948.675 6443.664 5332.287 7060.053
8  7313.0 7151.013 6763.533 7538.493 6237.130 8064.896
9  5035.4 5015.523 4822.893 5208.154 4165.731 5865.315
10 4322.6 4578.100 4349.549 4806.650 3719.452 5436.747
11 6389.5 6320.986 6057.644 6584.328 5452.430 7189.542
12 4152.2 4011.888 3709.980 4313.796 3130.873 4892.904
13 5544.8 4854.964 4652.116 5057.813 4002.798 5707.131
14 6095.1 5946.538 5726.896 6166.179 5090.218 6802.857
15 3626.2 3821.828 3491.525 4152.130 2930.682 4712.973
16 3745.4 4074.296 3781.397 4367.196 3196.327 4952.266
17 5121.8 5888.101 5674.071 6102.132 5033.204 6742.998
18 5674.5 5747.967 5545.680 5950.254 4895.934 6600.000
19 4256.6 4043.660 3746.360 4340.960 3164.212 4923.107
20 5803.7 6008.946 5782.898 6234.994 5150.961 6866.931

绘制图
> x0 <- seq(min(example9_1$广告支出),max(example9_1$广告支出))
> con_int<-predict(md, data.frame(广告支出=x0), interval="confidence", level=0.95)
> pre_int<-predict(md, data.frame(广告支出=x0), interval="prediction", level=0.95)
> par(cex=0.7)
> plot(example9_1[,3], example9_1[,2], xlab="广告支出", ylab="销售收入",family = 'SimSun')
> 
> abline(lm(example9_1[,2]~example9_1[,3]), lwd=2)
> lines(x0, con_int[,2],lty=2, lwd=2, col='blue')
> lines(x0, con_int[,3],lty=2, lwd=2, col='blue')
> lines(x0, pre_int[,2],lty=2, lwd=2, col='red')
> lines(x0, pre_int[,3],lty=2, lwd=2, col='red')
> legend(x="topleft", legend=c("回归线","置信区间"，"预测区间"),lty=1:3,lwd=2,cex=0.7)
个别值的预测区间：
> x0<-data.frame(广告支出=500)
> predict(md, newdata=x0)
       1 
5180.621 
> predict(md, x0, interval="confidence", level=0.95)
       fit      lwr      upr
1 5180.621 4994.127 5367.115
> predict(md, x0, interval="prediction", level=0.95)
       fit      lwr      upr
1 5180.621 4332.199 6029.043
>

4 对回归方程进行诊断

4.1 残差（yi(实际值) -yi(估计值)）与残差图

预测值（pre）, 残差（res）,标准化残差（zre）
> pre <-fitted(md)
> res<-residuals(md)
> zre<-md$residuals/(sqrt(deviance(md)/df.residual(md)))
> output<-data.frame(y=example9_1$销售收入, pre, res, zre)
> output
        y      pre        res        zre
1  4597.5 4264.925  332.57536  0.8441934
2  6611.0 6945.066 -334.06646 -0.8479784
3  7349.3 6448.639  900.66117  2.2861954
4  5525.7 5260.049  265.65073  0.6743151
5  4675.9 4763.054  -87.15430 -0.2212283
6  4418.6 4762.487 -343.88696 -0.8729063
7  5845.4 6196.170 -350.76993 -0.8903777
8  7313.0 7151.013  161.98700  0.4111801
9  5035.4 5015.523   19.87679  0.0504543
10 4322.6 4578.100 -255.49955 -0.6485479
11 6389.5 6320.986   68.51398  0.1739126
12 4152.2 4011.888  140.31161  0.3561603
13 5544.8 4854.964  689.83567  1.7510460
14 6095.1 5946.538  148.56225  0.3771033
15 3626.2 3821.828 -195.62753 -0.4965716
16 3745.4 4074.296 -328.89643 -0.8348550
17 5121.8 5888.101 -766.30113 -1.9451423
18 5674.5 5747.967  -73.46670 -0.1864844
19 4256.6 4043.660  212.94024  0.5405174
20 5803.7 6008.946 -205.24580 -0.5209861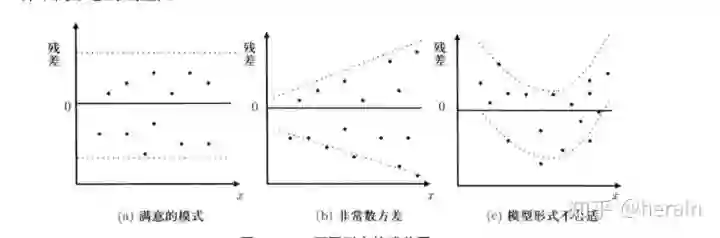

4.2 检验模型假定

4.2.1 检验线性关系（F检验，残差图）

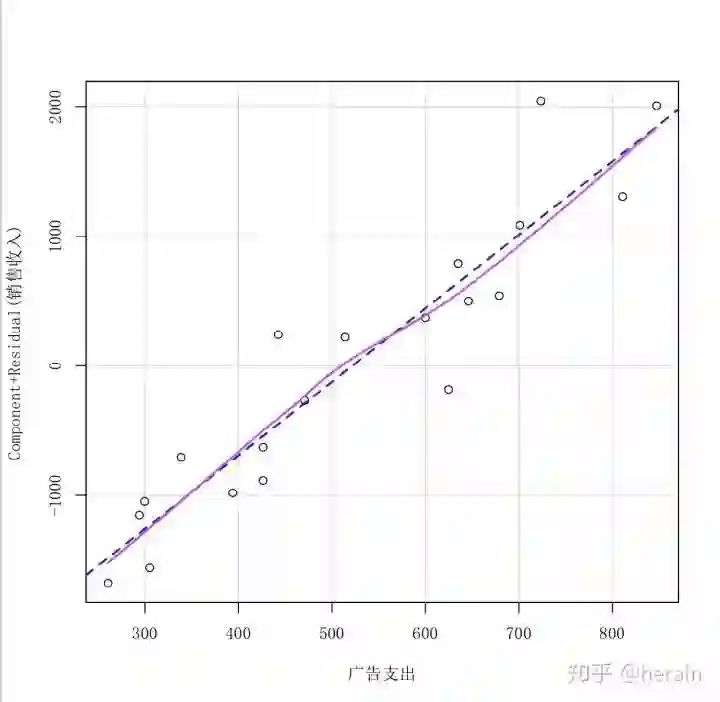
绘制残差图
> crPlots(md)
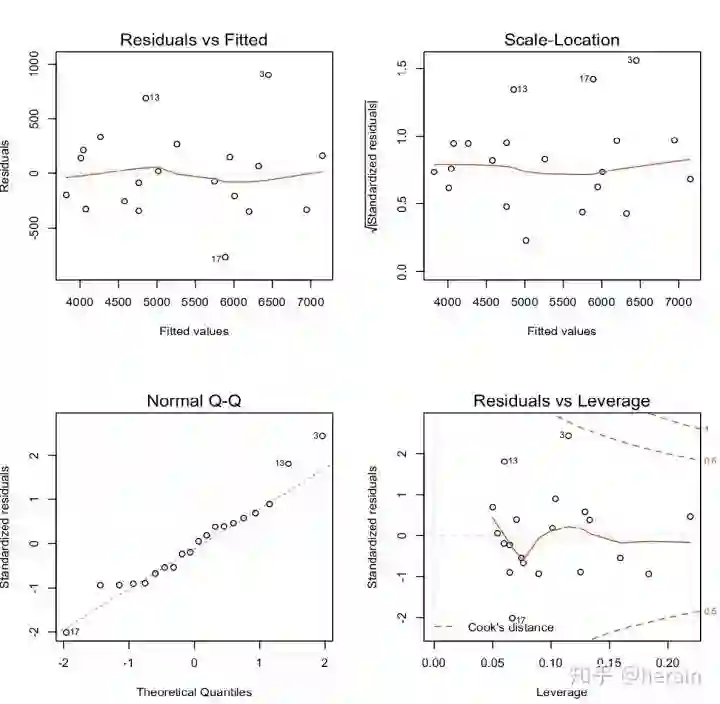
> crPlots(md,family = 'SimSun')

4.2.2 检验正态性（残差Q-Q图）

> par(mfcol=c(2,2), cex=0.7)
> plot(md)

4.2.3 检验方差齐性

检验方差齐性
> library(car)
> ncvTest(md)
Non-constant Variance Score Test 
Variance formula: ~ fitted.values 
Chisquare = 1.126441, Df = 1, p = 0.28854
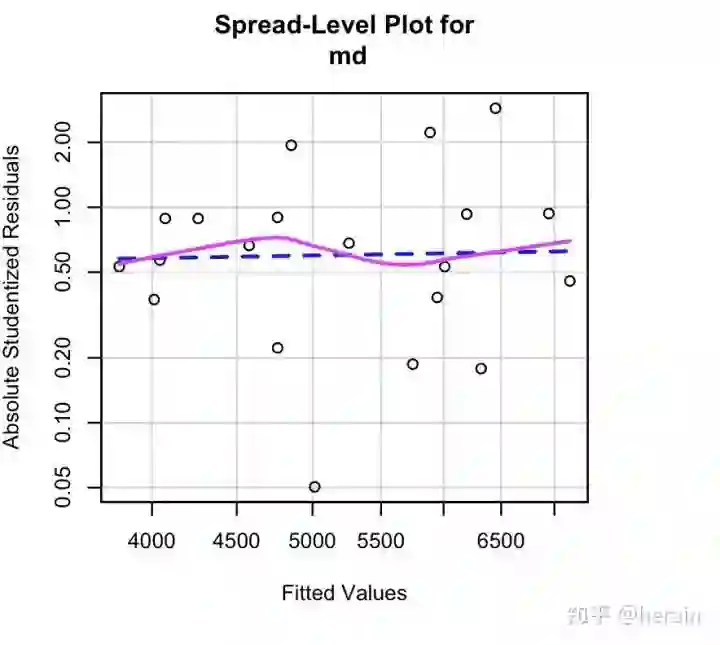
绘制散步 --水平图
spreadLevelPlot(md)

4.2.4 检验独立性

> durbinWatsonTest(md)
 lag Autocorrelation D-W Statistic p-value
   1       0.1330482      1.679232    0.44
 Alternative hypothesis: rho != 0

验证步骤省略：检测P值等于 0.44，不拒绝原假设，表名残差无自相关性。

写在最后：

至此，一元线性回归方程的完成，欢迎大家指正，请各位多多转发，给我好看。

公众号后台回复关键字即可学习

回复爬虫         爬虫三大案例实战
回复 Python 1小时破冰入门

回复数据挖掘   R语言入门及数据挖掘
回复人工智能   三个月入门人工智能
回复数据分析师   数据分析师成长之路
回复机器学习      机器学习的商业应用
回复数据科学      数据科学实战
回复常用算法      常用数据挖掘算法