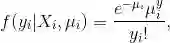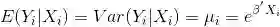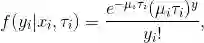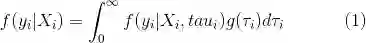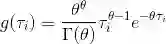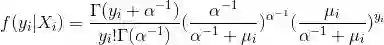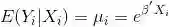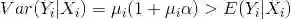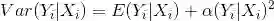数据分析师应该知道的16种回归方法：负二项回归

本篇分享这个系列的第二种计数回归方法：负二项回归。同泊松计数回归不同是，在负二项回归中假设方差大于均值，这种情形为通常称为过度离散(overdispersion)，相反，若方差小于均值，称之为低扩散(underdispersion)。负二项回归可以有效地对过离散数据建模，下节要讲的准泊松回归可以对这两种分散问题建模。下面先简单介绍负二项回归的相关理论，然后给出具体案例。

对于观测数据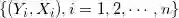，若采用泊松回归，则有

在负二项回归中，我们假定

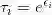
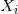
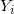
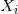
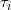
其中表示不可观测的随机效应，与回归自变量相互独立。此时，在和下服从条件均值和条件方差都为的泊松分布，即

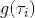
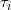
设为的概率密度函数，则

对于上述积分，为得到解析表达式，在传统的负二项回归中，通常假设,则

将上式带入(1),可得如下负二项分布

其中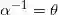。此负二项分布的条件均值为

条件方差分别为

易见，这个负二项回归模型的方差为均值的二次函数，因此也被称为NB2模型。当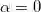时，NB2模型退化为泊松回归模型。负二项回归的系数可通过牛顿迭代法获得，在R中利用MASS包的glm.nb函数求取。最后一个问题，对于计数型数据集，如何判断它是否过度离散。因为在NB2中

而在泊松回归中均值和方差相等，因此只需判断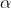是否等于0，可通过R中的AER::dispersiontest函数实现。具体的推导过程可参见Cameron和Trivedi在1990对这一问题的论述。

案例

MASS包中的quie数据集描述了新南威尔士农村学校旷课情况，该数据集记录146个学生的宗教信仰(Eth), 性别(Sex),年龄(Age) ,学习状态(Lrn),旷课天数(Days)五个指标。我们想通过这一数据集合研究旷课天数与其他因素之间的关系。

library(MASS)
library(AER)
library(COUNT)

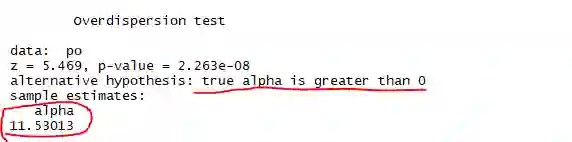
首先检查数据是否过度离散，先进行泊松回归，然后使用dispersiontest函数对泊松回归结果进行检测，看alpha是否大于0，注意需设置dispersiontest函数中的trafo=1，否则认为alpha大于1过离散。

po <- glm(Days ~ Sex+Age + Eth +Lrn, data = quine,
             family=poisson)
dispersiontest(po,trafo=1)

过离散测试中alpha=11.53013,因此泊松回归不能有效反映这组数据真实特征，下面采用负二项回归研究这组数据

nb <- glm.nb(Days ~ Sex+Age + Eth + Lrn, data = quine)
list(nb=unlist(modelfit(nb)),po=unlist(modelfit(po)))

结果表明，对于quie数据集，在各项指标下，负二项回归都远比泊松回归好。

推荐阅读

数据分析师应该知道的16种回归方法：泊松回归

据分析师应该知道的16种回归方法：定序回归

reticulate: R interface to Python

谈谈大数据的那点事 （12）——如何理解大数据和分析大数据

从零开始深度学习第10讲：三维卷积、池化与全连接

R语言做并行爬虫（案例说明）

R语言爬虫常用方法总结（以案例说明）

使用jupyter notebook搭建数据科学最佳交互式环境

长按二维码关注“数萃大数据”