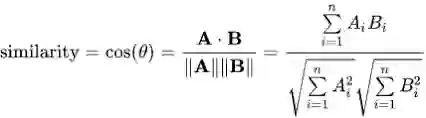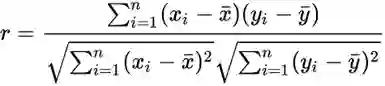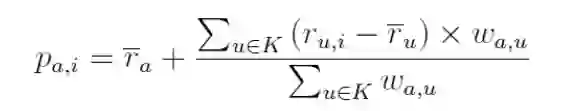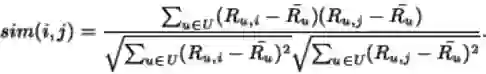【干货】基于协同过滤的推荐系统实战（附完整代码）

2018 年 4 月 5 日 专知 Yingying

【导读】本文使用Python实现简单的推荐系统，分别实践了基于用户和基于商品的推荐系统，代码使用sklearn工具包实现。除了代码实现外，还分别从理论上介绍了两种推荐系统原理：User-Based Collaborative Filtering 和 Item-Based Collaborative Filtering，并讲解了几种常见的相似性度量方法及它们分别适用场景，还实现了推荐系统的评估。最终分析两种推荐系统的优劣，说明混合推荐技术可能具有更好的性能。

作者 | Chhavi Saluja

编译 | 专知

参与 | Yingying

基于协同过滤的推荐系统

在这篇文章中，我使用Python实现一个简单的推荐系统。

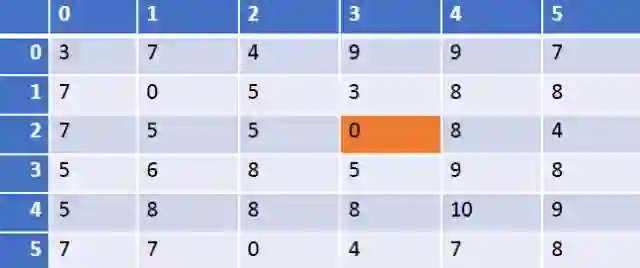
给定下面的用户商品user-item评分矩阵M，其中6个用户（行）评价了6个商品（列）。评分可以为1-10的整数值，0表示评分不存在。（请注意，我们在Python中使用从零开始的行和列索引，但对于用户输入，user_id将占用1-6和1-6的item_id）。假设，我们必须找出用户3是否喜欢第4项商品。因此用户3成为我们的目标用户或活跃用户，项目4是目标商品。

代码如下：

#M is user-item ratings matrix where ratings are integers from 1-10
M = np.asarray([[3,7,4,9,9,7], 
                [7,0,5,3,8,8],
               [7,5,5,0,8,4],
               [5,6,8,5,9,8],
               [5,8,8,8,10,9],
               [7,7,0,4,7,8]])
M=pd.DataFrame(M)

#declaring k,metric as global which can be changed by the user later
global k,metric
k=4
metric='cosine' #can be changed to 'correlation' for 
Pearson correlation similaries

基于用户的协同过滤

首先，我们必须预测用户3对第4项商品的评分。在基于用户的推荐系统中，我们会找到3个与用户3最相似的用户，并用这三个用户的评分预测用户3对第4项商品的评分。

常用的相似性度量是余弦，皮尔森（Pearson），欧几里得等等。我们将在这里使用余弦相似性，其定义如下：

而且， Pearson相关性定义为：

在sklearn中，NearestNeighbors方法可用于基于各种相似性度量搜索k个最近邻。

代码如下:

#This function finds k similar users given the user_id and ratings 
matrix M
#Note that the similarities are same as obtained via using 
pairwise_distances
def findksimilarusers(user_id, ratings, metric = metric, k=k):
    similarities=[]
    indices=[]
    model_knn = NearestNeighbors(metric = metric, algorithm = 'brute') 
    model_knn.fit(ratings)

    distances, indices = model_knn.kneighbors(ratings.iloc[user_id-1, :]
    .values.reshape(1, -1), n_neighbors = k)
    similarities = 1-distances.flatten()
    print '{0} most similar users for User {1}:\n'.format(k-1,user_id)
    for i in range(0, len(indices.flatten())):
        if indices.flatten()[i]+1 == user_id:
            continue;

        else:
            print '{0}: User {1}, with similarity of {2}'.
            format(i, indices.flatten()[i]+1, similarities.flatten()[i])
            
    return similarities,indices

def predict_userbased(user_id, item_id, ratings, metric = metric, k=k):
    prediction=0
    similarities, indices=findksimilarusers(user_id, ratings,metric, k)
     #similar users based on cosine similarity
    mean_rating = ratings.loc[user_id-1,:].mean() 
     #to adjust for zero based indexing
    sum_wt = np.sum(similarities)-1
    product=1
    wtd_sum = 0 
    
    for i in range(0, len(indices.flatten())):
        if indices.flatten()[i]+1 == user_id:
            continue;
        else: 
            ratings_diff = ratings.iloc[indices.flatten()[i],item_id-1]
            -np.mean(ratings.iloc[indices.flatten()[i],:])
            product = ratings_diff * (similarities[i])
            wtd_sum = wtd_sum + product
    
    prediction = int(round(mean_rating + (wtd_sum/sum_wt)))
    print '\nPredicted rating for user {0} -> item {1}: {2}'.
    format(user_id,item_id,prediction)

    return prediction

findksimilarusers函数使用这个方法为目标用户返回k个最接近邻的相似性和索引。基于用户的推荐系统方法，基于predict_user的函数进一步预测用户3对于商品4的评分。预测通过邻居平均值的偏差的加权平均值来计算，并将其添加到目标用户的平均评分中。偏差用于调整用户相关的偏差。出现用户偏差的原因是某些用户可能总是对所有项目给予高评分或低评分。

其中p(a,i)是目标用户a对商品i的预测，w(a,u)是用户a和u之间的相似度，K是和目标用户相似的K个用户。

基于商品（Item-Based）的协同过滤

在这种方法中，使用余弦相似性度量来计算一对商品之间的相似度。可以通过使用简单的加权平均值来预测目标用户a对目标商品i的评分：

#This function finds k similar items given the item_id and ratings 
matrix M

def findksimilaritems(item_id, ratings, metric=metric, k=k):
    similarities=[]
    indices=[]    
    ratings=ratings.T
    model_knn = NearestNeighbors(metric = metric, algorithm = 'brute')
    model_knn.fit(ratings)

    distances, indices = model_knn.kneighbors(ratings.iloc[item_id-1, :]
    .values.reshape(1, -1), n_neighbors = k)
    similarities = 1-distances.flatten()
    print '{0} most similar items for item {1}:\n'.format(k-1,item_id)
    for i in range(0, len(indices.flatten())):
        if indices.flatten()[i]+1 == item_id:
            continue;

        else:
            print '{0}: Item {1} :, with similarity of {2}'
.format(i,indices.flatten()[i]+1, similarities.flatten()[i])


    return similarities,indices

#This function predicts the rating for specified user-item combination 
based on item-based approach
def predict_itembased(user_id, item_id, ratings, metric = metric, k=k):
    prediction= wtd_sum =0
    similarities, indices=findksimilaritems(item_id, ratings) 
    #similar users based on correlation coefficients
    sum_wt = np.sum(similarities)-1
    product=1
    
    for i in range(0, len(indices.flatten())):
        if indices.flatten()[i]+1 == item_id:
            continue;
        else:
            product = ratings.iloc[user_id-1,indices.flatten()[i]] * 
            (similarities[i])
            wtd_sum = wtd_sum + product                              
    prediction = int(round(wtd_sum/sum_wt))
    print '\nPredicted rating for user {0} -> item {1}: {2}'
.format(user_id,item_id,prediction)      

    return prediction

在上述代码中，函数findksimilaritems使用最近邻方法采用余弦相似性来找到k项最相似的商品i。函数predict_itembased进一步预测用户3将使用基于商品的CF方法（上面的公式）给予商品4的评分。

调整后的余弦相似度

使用基于商品的推荐系统方法的余弦相似性度量不考虑用户评分的偏差。调整后的余弦相似度通过从每个共同评分对中减去各自用户的平均评分来抵消该缺点，并且被定义为如下

为了在Python中实现Adjusted Cosine相似度，我定义了一个名为computeAdjCosSim的简单函数，该函数返回调整后的余弦相似度矩阵，给出评分矩阵。函数findksimilaritems_adjcos和predict_itembased_adjcos利用调整后的余弦相似度来查找k个相似项并计算预测评分。

函数recommendItem提示用户选择推荐方法（基于用户（余弦），基于用户（相关），基于商品（余弦），基于商品（调整余弦，Adjusted Cosine Similarity）。基于所选方法和相似性度量，该函数可以预测指定用户和商品的评分，并建议商品是否可以推荐给用户，如果该商品尚未被用户评分，并且预测评分大于6，则推荐给用户，如果评分小于6，则不推荐给用户。

代码如下：

This function is used to compute adjusted cosine similarity matrix for 
items
def computeAdjCosSim(M):
    sim_matrix = np.zeros((M.shape[1], M.shape[1]))
    M_u = M.mean(axis=1) #means
          
    for i in range(M.shape[1]):
        for j in range(M.shape[1]):
            if i == j:
                
                sim_matrix[i][j] = 1
            else:                
                if i<j:
                    
                    sum_num = sum_den1 = sum_den2 = 0
                    for k,row in M.loc[:,[i,j]].iterrows(): 

                        if ((M.loc[k,i] != 0) & (M.loc[k,j] != 0)):
                            num = (M[i][k]-M_u[k])*(M[j][k]-M_u[k])
                            den1= (M[i][k]-M_u[k])**2
                            den2= (M[j][k]-M_u[k])**2
                            
                            sum_num = sum_num + num
                            sum_den1 = sum_den1 + den1
                            sum_den2 = sum_den2 + den2
                        
                        else:
                            continue                          
                                       
                    den=(sum_den1**0.5)*(sum_den2**0.5)
                    if den!=0:
                        sim_matrix[i][j] = sum_num/den
                    else:
                        sim_matrix[i][j] = 0


                else:
                    sim_matrix[i][j] = sim_matrix[j][i]           
            
    return pd.DataFrame(sim_matrix)

#This function finds k similar items given the item_id and ratings
matrix M

def findksimilaritems_adjcos(item_id, ratings, k=k):
    
    sim_matrix = computeAdjCosSim(ratings)
    similarities = sim_matrix[item_id-1].sort_values(ascending=False)
    [:k].values
    indices = sim_matrix[item_id-1].sort_values(ascending=False)[:k].
    index
    
    print '{0} most similar items for item {1}:\n'.format(k-1,item_id)
    for i in range(0, len(indices)):
            if indices[i]+1 == item_id:
                continue;

            else:
                print '{0}: Item {1} :, with similarity of {2}'
.format(i,indices[i]+1, similarities[i])
        
    return similarities ,indices

#This function predicts the rating for specified user-item combination 
for adjusted cosine item-based approach
#As the adjusted cosine similarities range from -1,+1, sometimes the 
predicted rating can be negative or greater than max value
#Hack to deal with this: Rating is set to min if prediction is negative, 
Rating is set to max if prediction is above max
def predict_itembased_adjcos(user_id, item_id, ratings):
    prediction=0

    similarities, indices=findksimilaritems_adjcos(item_id, ratings) 
    #similar users based on correlation coefficients
    sum_wt = np.sum(similarities)-1

    product=1
    wtd_sum = 0 
    for i in range(0, len(indices)):
        if indices[i]+1 == item_id:
            continue;
        else:
            product = ratings.iloc[user_id-1,indices[i]] * 
            (similarities[i])
            wtd_sum = wtd_sum + product                              
    prediction = int(round(wtd_sum/sum_wt))
    if prediction < 0:
        prediction = 1
    elif prediction >10:
        prediction = 10
    print '\nPredicted rating for user {0} -> item {1}: {2}'
.format(user_id,item_id,prediction)      
        
    return prediction

#This function utilizes above function to recommend items for selected 
approach. Recommendations are made if the predicted
#rating for an item is greater than or equal to 6, and the items has not 
been rated already
def recommendItem(user_id, item_id, ratings):
    
    if user_id<1 or user_id>6 or type(user_id) is not int:
        print 'Userid does not exist. Enter numbers from 1-6'
    else:    
        ids = ['User-based CF (cosine)','User-based CF (correlation)',
'Item-based CF (cosine)', 'Item-based CF (adjusted cosine)']

        approach = widgets.Dropdown(options=ids, value=ids[0],
               description='Select Approach', width='500px')
        
        def on_change(change):
            prediction = 0
            clear_output(wait=True)
            if change['type'] == 'change' and change['name'] == 'value':            
                if (approach.value == 'User-based CF (cosine)'):
                    metric = 'cosine'
                    prediction = predict_userbased(user_id, 
item_id, ratings, metric)
                elif (approach.value == 'User-based CF (correlation)') :                       
                    metric = 'correlation'               
                    prediction = predict_userbased(user_id,
item_id, ratings, metric)
                elif (approach.value == 'Item-based CF (cosine)'):
                    prediction = predict_itembased(user_id, item_id, 
ratings)
                else:
                    prediction = predict_itembased_adjcos(user_id,
item_id,ratings)

                if ratings[item_id-1][user_id-1] != 0: 
                    print 'Item already rated'
                else:
                    if prediction>=6:
                        print '\nItem recommended'
                    else:
                        print 'Item not recommended'

        approach.observe(on_change)
        display(approach)

相似性度量的选择

在选择相似性度量时，可根据以下几点进行选择：

• 当您的数据受用户偏好/用户的不同评分尺度影响时，请使用皮尔逊相似度

• 如果数据稀疏，则使用余弦（许多额定值未定义）

• 如果您的数据不稀疏并且属性值的大小很重要，请使用欧几里得（Euclidean）。

• 建议使用调整后的余弦（Adjusted Cosine Similarity）进行基于商品的方法来调整用户偏好。

评估推荐系统

评估推荐系统有很多评估指标。然而，最常用的是RMSE（均方根误差）。函数evaluateRS使用sklearn的mean_squared_error函数计算预测评级与实际评级之间的RMSE，并显示所选方法的RMSE值。（为了简化说明，使用了小数据集，因此尚未将其分为训练集和测试集;本文中也未考虑交叉验证）。

代码如下:

#This is final function to evaluate the performance of selected 
recommendation approach and the metric used here is RMSE
#suppress_stdout function is used to suppress the print outputs of all 
the functions inside this function. It will only print 
#RMSE values
def evaluateRS(ratings):
    ids = ['User-based CF (cosine)','User-based CF (correlation)',
'Item-based CF (cosine)','Item-based CF (adjusted cosine)']
    approach = widgets.Dropdown(options=ids, value=ids[0],
description='Select Approach', width='500px')
    n_users = ratings.shape[0]
    n_items = ratings.shape[1]
    prediction = np.zeros((n_users, n_items))
    prediction= pd.DataFrame(prediction)
    def on_change(change):
        clear_output(wait=True)
        with suppress_stdout():
            if change['type'] == 'change' and change['name'] == 'value':            
                if (approach.value == 'User-based CF (cosine)'):
                    metric = 'cosine'
                    for i in range(n_users):
                        for j in range(n_items):
                            prediction[i][j] = predict_userbased(i+1, 
j+1, ratings, metric)
                elif (approach.value == 'User-based CF (correlation)') :                       
                    metric = 'correlation'               
                    for i in range(n_users):
                        for j in range(n_items):
                            prediction[i][j] = predict_userbased(i+1, 
j+1, ratings, metric)
                elif (approach.value == 'Item-based CF (cosine)'):
                    for i in range(n_users):
                        for j in range(n_items):
                            prediction[i][j] = predict_userbased(i+1, 
j+1, ratings)
                else:
                    for i in range(n_users):
                        for j in range(n_items):
                            prediction[i][j] = predict_userbased(i+1, 
j+1, ratings)
              
        MSE = mean_squared_error(prediction, ratings)
        RMSE = round(sqrt(MSE),3)
        print "RMSE using {0} approach is: {1}".format(approach.value,
RMSE)
              
    approach.observe(on_change)
    display(approach)