深度学习即将非法？欧盟《一般数据保护条例》五月生效

2018 年 1 月 31 日 深度学习世界

选自Analytics India

作者：Richa Bhatia

机器之心编译

《欧盟一般数据保护条例》（General Data Protection Regulation，GDPR）是 20 年来数据隐私条例的最重要变化，它将取代《欧盟个人资料保护指令》95/46/EC，并将协调全欧洲的数据隐私法律，为所有欧盟民众保护和授权数据隐私，并将重塑整个地区的数据隐私保护形式。在 GDPR 中，有关「算法公平性」的条款要求所有公司必须对其算法的自动决策进行解释，这意味着目前大量 AI 应用依赖的深度学习算法不再符合法规。

GDPR 的重点内容，以及它对商业的影响，可在其官方网站上找到：https://www.eugdpr.org/

几个月后，《一般数据保护条例》（GDPR）将生效，这被认为是对人工智能应用于商业的方式的一次彻底整改。2018 年 5 月 25 日，GDPR 将在欧盟全面实施。

113 天后就要到来的 Deadline 引起了 AI 社区和技术巨头的争论，他们现在正在努力满足欧盟的数据隐私和算法公平性原则。而对于欧盟公民来说，GDPR 统一数据保护法规，增加技术公司在收集用户数据时的责任，从而保护了公民权利。

在 GDPR 的网站上有一个时钟：再过 113 天该条例就将在全欧盟生效了。

GDPR 即将实施引起了很多人工智能学界人士的关注，《终极算法》作者，华盛顿大学教授 Pedro Domingos 在社交网络中说道：「自 5 月 25 日起，欧盟将会要求所有算法解释其输出原理，这意味着深度学习成为非法的方式。」

即将到来的规定将欧洲分成两大阵营：拥抱数据隐私和算法公平性原则的社会公民；对此不满的技术巨头，因为它们将面临新的挑战，如需要征求用户同意、处理 AI 的黑箱问题，这些问题可能最终导致 AI 相关应用不再合法，违者将接受全球营业额 4% 的罚款。

GDPR 要点概述

规定针对从欧盟公民处收集数据的企业：该规定不限于总部在欧盟地区的企业，而是覆盖到从欧盟公民处收集数据的所有组织。GDPR 要求此类企业反思其条款和条件（解释该公司如何使用个人数据来销售广告）中的内容，强制企业遵循 Privacy by Design 原则。

数据转移权：该规定声明，用户可要求自己的个人数据畅通无阻地直接迁移至新的提供商，数据以机器可读的格式迁移。这类似于在不丢失任何数据的情况下更改移动运营商或社交网络。对于谷歌、Facebook 等名副其实的数据挖掘公司和较小的数据科学创业公司而言，这就像是敲响了丧钟，当用户不再使用该公司产品时，它们将会丢失大量数据。

被遗忘权：GDPR 第 17 条强调，每个数据主体有权要求数据控制者删除个人数据，并且不能过分延长数据留存时间，控制者有义务遵循该规定。这对以 cookie 形式收集数据、从定向投放广告中获取收益的技术巨头而言是一项巨大损失。

算法公平性：自动决策的可解释权（The Right to Explanation of Automated Decision）指出数据主体有权要求算法自动决策给出解释，有权在对算法决策不满意时选择退出。例如，如果贷款申请人被自动决策拒绝时，有权寻求解释。对于技术公司而言，这是对人工智能的严重限制，将大幅减缓 AI 技术的发展。

AI 的高性能 vs 难解释性难题

在这里，我们不想深入研究欧盟指导方针的本质，但有必要指出目前被广泛应用的人工智能技术所面临的最大批评——深度学习及其不可解释性（即黑箱状态）。这可能会导致任何 AI 公司无法开展已有业务，甚至会被认为非法。目前，人工智能专家和科技公司从数据中获益，但又不断声称这些算法因为架构的复杂性而难以解释其输出的生成原理。

著名学者 Dr. PK Viswanathan 曾对人工神经网络的黑箱问题进行过研究。根据他的介绍，人们普遍认为神经网络是一个黑箱，但其机制并非完全不可解释，仍有一些分析其原理的方法。

例如，对于预测和分类问题，与 logistic 回归、随机森林等其他基于统计的有监督技术不同，神经网络是非参数、非线性的复杂关系模型，被认为具备泛逼近性。神经网络被用于所有分类和预测问题。神经网络的一些常见应用甚至包括：决定是否购买金融市场的产品，以及对风险进行判断。

人工神经网络的拓扑学

我们讨论两个隐藏层的多层感知机（一种前馈人工神经网络）。两个隐藏层的多层感知机因其预测准确率而知名。在两个隐藏层的多层感知机中，有两个输入神经元、两个隐藏层和四个节点，然后给出输出。网络初始化权重、偏置项、数值，激活函数可设定为 sigmoid 函数（或 logistic 函数），你可以用前馈方法改变权重的值。

在其架构中，隐藏层和黑箱点以及神经网络学习训练数据的方式密切相关，这正是对其主要批判的来源。

神经网络的推理方法是通过迭代地最小化损失函数不断改变权重的值。这被称为黑箱难题，它可以逼近任何函数，但对预测变量和输出之间的关系不能给出任何解释，PK Viswanathan 说。在监督学习问题中，人们可以解释 x 和 y 之间的准确关系，但无法捕捉神经网络生成这些关系的运作方式。

人们对于神经网络的最大批判是：

它缺乏可解释力，我们无法确定隐藏层内部发生了什么。但是神经网络在近似值和精确度上普遍得分较高。
在现实世界中很难解释摘要权重（synoptic weight），但是在传统技术中却不是，这进一步加深了黑箱难题。

解决深度学习的黑箱难题

现在，许多研究者已经致力于解释神经网络如何做出决策。其中一些方法如下：

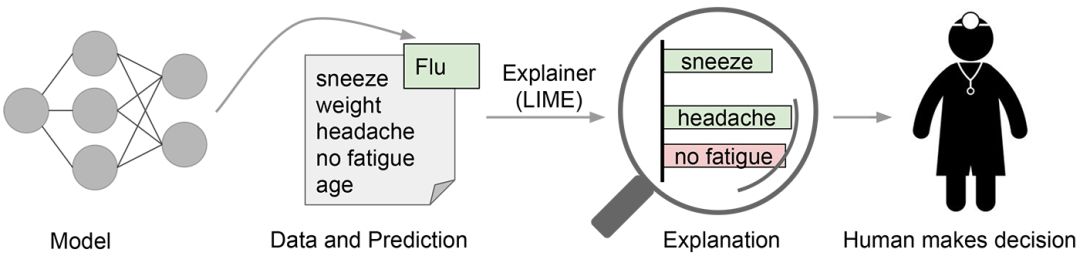
LIME：Local Interpretable Model-Agnostic Explanations 更广为所知的名称是 LIME，它是一个涉及以多种方式操作数据变量以查看什么把分值提高的最多的技术。在 LIME 中，局部指的是局部保真度，即解释应该反映分类器在被预测实例「周围」的行为。这一解释是无用的除非它是可阐释的——也就是说，除非人可以理解它。Lime 可以解释任何模型而无需深入它，因此它是模型不可知论的。

DARPA 的可解释性 AI（Explainable AI）：现在，DARPA 创建了一套机器学习技术来产生更可解释的模型，同时维持一个高水平的学习表现。可解释性 AI 可以使人类用户理解和管理即将到来的 AI 伙伴，其核心优势是新技术可以潜在地回避掉对额外层的需求。另一个解释组件可以从训练神经网络关联带有隐藏层节点的语义属性——这可以促进对可解释功能的学习。