会员服务

AI科学家带你从零开始学习：循环神经网络 ！

2017 年 11 月 29 日 全球人工智能


——免费加入AI技术专家社群>>

——免费加入AI高管投资者群>>

——日薪5k-10k招兼职AI讲师>>

－－全国招募1000名AI推广大使>>

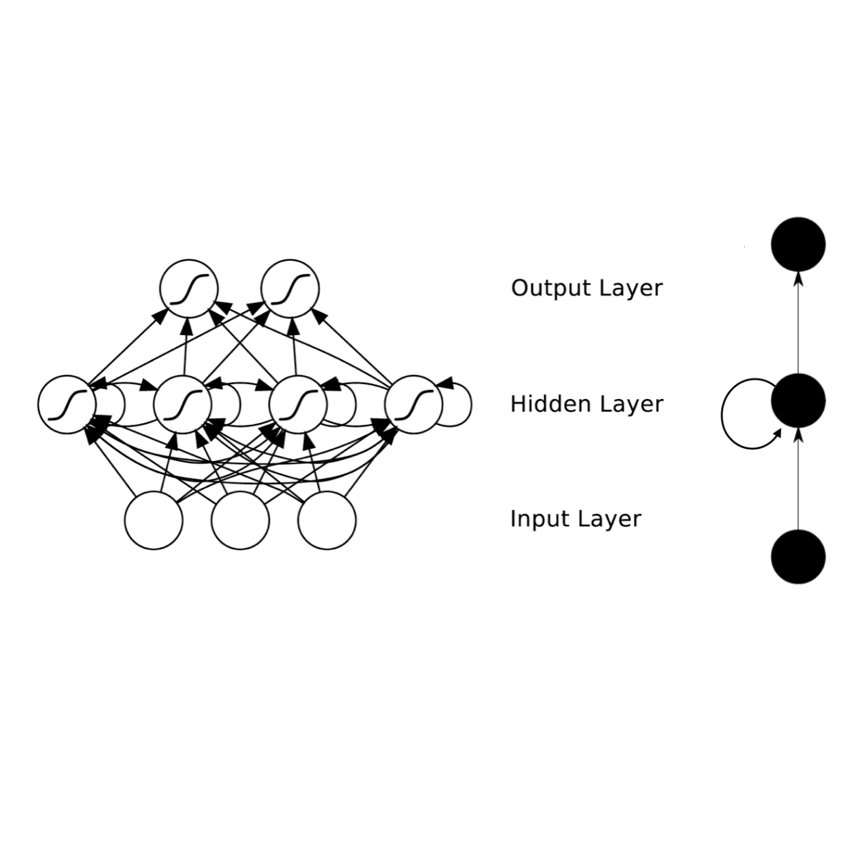
前面的教程里我们使用的网络都属于前馈神经网络。为什么叫前馈是整个网络是一条链（回想下gluon.nn.Sequential），每一层的结果都是反馈给下一层。这一节我们介绍循环神经网络，这里每一层不仅输出给下一层，同时还输出一个隐藏状态，给当前层在处理下一个样本时使用。下图展示这两种网络的区别。

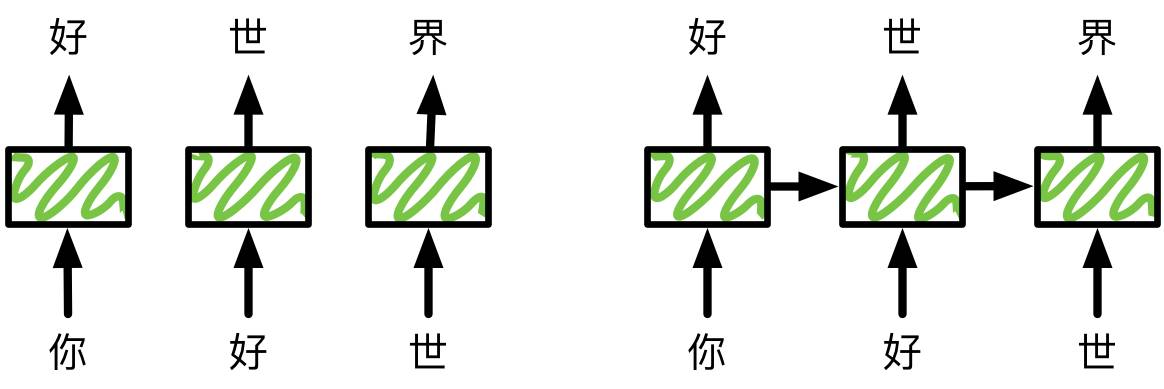
循环神经网络的这种结构使得它适合处理前后有依赖关系的样本。我们拿语言模型举个例子来解释这个是怎么工作的。语言模型的任务是给定句子的前T个字符，然后预测第T+1个字符。假设我们的句子是“你好世界”，使用前馈神经网络来预测的一个做法是，在时间1输入“你”，预测”好“，时间2向同一个网络输入“好”预测“世”。下图左边展示了这个过程。

注意到一个问题是，当我们预测“世”的时候只给了“好”这个输入，而完全忽略了“你”。直觉上“你”这个词应该对这次的预测比较重要。虽然这个问题通常可以通过n-gram来缓解，就是说预测第T+1个字符的时候，我们输入前n个字符。如果n=1，那就是我们这里用的。我们可以增大n来使得输入含有更多信息。但我们不能任意增大n，因为这样通常带来模型复杂度的增加从而导致需要大量数据和计算来训练模型。

循环神经网络使用一个隐藏状态来记录前面看到的数据来帮助当前预测。上图右边展示了这个过程。在预测“好”的时候，我们输出一个隐藏状态。我们用这个状态和新的输入“好”来一起预测“世”，然后同时输出一个更新过的隐藏状态。我们希望前面的信息能够保存在这个隐藏状态里，从而提升预测效果。

在更加正式的介绍这个模型前，我们先去弄一个比“你好世界“稍微复杂点的数据。

《时间机器》数据集

我们用《时间机器》这本书做数据集主要是因为古登堡计划计划使得可以免费下载，而且我们看了太多用莎士比亚作为例子的教程。下面我们读取这个数据并看看前面500个字符（char）是什么样的：

In [1]:
with open("../data/timemachine.txt") as f:
    time_machine = f.read()print(time_machine[0:500])
The Time Machine, by H. G. Wells [1898]




I


The Time Traveller (for so it will be convenient to speak of him)
was expounding a recondite matter to us. His grey eyes shone and
twinkled, and his usually pale face was flushed and animated. The
fire burned brightly, and the soft radiance of the incandescent
lights in the lilies of silver caught the bubbles that flashed and
passed in our glasses. Our chairs, being his patents, embraced and
caressed us rather than submitted to be sat upon, and the

接着我们稍微处理下数据集。包括全部改为小写，去除换行符，然后截去后面一段使得接下来的训练会快一点。

In [2]:
time_machine = time_machine.lower().replace('\n', '').replace('\r', '')
time_machine = time_machine[0:10000]

字符的数值表示

先把数据里面所有不同的字符拿出来做成一个字典：

In [3]:
character_list = list(set(time_machine))
character_dict = dict([(char,i) for i,char in enumerate(character_list)])

vocab_size = len(character_dict)

print('vocab size:', vocab_size)
print(character_dict)
vocab size: 43
{'x': 0, 'm': 1, 'o': 2, ')': 3, 'j': 4, 'h': 5, 'w': 6, 'l': 7, ':': 8, '-': 9, 'q': 10, 'k': 11, '!': 12, 'c': 13, '[': 14, "'": 15, 'p': 16, '9': 17, 'n': 18, '1': 19, 's': 20, 'a': 21, 'e': 22, '.': 23, ']': 24, '?': 25, ';': 26, 'd': 27, 'i': 28, '8': 29, 'f': 30, 'u': 31, ',': 32, ' ': 33, 'y': 34, 'z': 35, 'g': 36, '(': 37, 't': 38, '_': 39, 'r': 40, 'v': 41, 'b': 42}

然后可以把每个字符转成从0开始的指数(index)来方便之后的使用。

In [4]:
time_numerical = [character_dict[char] for char in time_machine]

sample = time_numerical[:40]

print('chars: \n', ''.join([character_list[idx] for idx in sample]))
print('\nindices: \n', sample)
chars:
 the time machine, by h. g. wells [1898]i

indices:
 [38, 5, 22, 33, 38, 28, 1, 22, 33, 1, 21, 13, 5, 28, 18, 22, 32, 33, 42, 34, 33, 5, 23, 33, 36, 23, 33, 6, 22, 7, 7, 20, 33, 14, 19, 29, 17, 29, 24, 28]

数据读取

同前一样我们需要每次随机读取一些（batch_size个）样本和其对用的标号。这里的样本跟前面有点不一样，这里一个样本通常包含一系列连续的字符（前馈神经网络里可能每个字符作为一个样本）。

如果我们把序列长度（seq_len）设成10，那么一个可能的样本是The Time T。其对应的标号仍然是长为10的序列，每个字符是对应的样本里字符的后面那个。例如前面样本的标号就是he Time Tr。

下面代码每次从数据里随机采样一个批量：

In [5]:
import random
from mxnet import nd
def data_iter(batch_size, seq_len, ctx=None):
    num_examples = (len(time_numerical)-1) // seq_len
    num_batches = num_examples // batch_size
    # 随机化样本
    idx = list(range(num_examples))
    random.shuffle(idx)
    # 返回seq_len个数据
    def _data(pos):
        return time_numerical[pos:pos+seq_len]
    for i in range(num_batches):
        # 每次读取batch_size个随机样本
        i = i * batch_size
        examples = idx[i:i+batch_size]
        data = nd.array(
            [_data(j*seq_len) for j in examples], ctx=ctx)
        label = nd.array(
            [_data(j*seq_len+1) for j in examples], ctx=ctx)
        yield data, label

看下读出来长什么样：

In [6]:
for data, label in data_iter(batch_size=3, seq_len=8):
    print('data: ', data, '\n\nlabel:', label)
    break
data:
[[ 40.   2.  18.  36.  33.  20.  28.  27.]
 [ 33.  38.  28.   1.  22.  33.  38.  40.]
 [  2.  41.  28.  18.  13.  28.  21.   7.]]
<NDArray 3x8 @cpu(0)>

label:
[[  2.  18.  36.  33.  20.  28.  27.  22.]
 [ 38.  28.   1.  22.  33.  38.  40.  21.]
 [ 41.  28.  18.  13.  28.  21.   7.  33.]]
<NDArray 3x8 @cpu(0)>

循环神经网络

在对输入输出数据有了解后，我们来正式介绍循环神经网络。首先回忆下单隐层的前馈神经网络的定义，假设隐层的激活函数是