置信学习:让样本中的"脏数据"原形毕露 ( 附开源实现 )

文章作者:娄杰 LinkDoc
内容来源:高能NLP@知乎
在实际工作中,你是否遇到过这样一个问题或痛点:无论是通过哪种方式获取的标注数据,数据标注质量可能不过关,存在一些错误?亦或者是数据标注的标准不统一、存在一些歧义?特别是badcase反馈回来,发现训练集标注的居然和badcase一样?如下图所示,QuickDraw、MNIST和Amazon Reviews数据集中就存在错误标注。

为了快速迭代,大家是不是常常直接人工去清洗这些“脏数据”?(笔者也经常这么干~)。但数据规模上来了咋整?有没有一种方法能够自动找出哪些错误标注的样本呢?基于此,本文尝试提供一种可能的解决方案——置信学习。

01
置信学习的定义
那什么是置信学习呢?这个概念来自一篇由MIT和Google联合提出的paper:《Confident Learning: Estimating Uncertainty in Dataset Labels[1] 》。论文提出的置信学习(confident learning,CL)是一种新兴的、具有原则性的框架,以识别标签错误、表征标签噪声并应用于带噪学习(noisy label learning)。
笔者注:笔者乍一听置信学习挺陌生的,但回过头来想想,好像干过类似的事情,比如:在某些场景下,对训练集通过交叉验证来找出一些可能存在错误标注的样本,然后交给人工去纠正。此外,神经网络的成功通常建立在大量、干净的数据上,标注错误过多必然会影响性能表现,带噪学习可是一个大的topic,有兴趣可参考这些文献: github.com/subeeshvasu/。
废话不说,首先给出这种置信学习框架的优势:
最大的优势:可以用于发现标注错误的样本!
无需迭代,开源了相应的python包,方便快速使用!在ImageNet中查找训练集的标签错误仅仅需要3分钟!
可直接估计噪声标签与真实标签的联合分布,具有理论合理性。
不需要超参数,只需使用交叉验证来获得样本外的预测概率。
不需要做随机均匀的标签噪声的假设(这种假设在实践中通常不现实)。
与模型无关,可以使用任意模型,不像众多带噪学习与模型和训练过程强耦合。
笔者注:置信学习找出的「标注错误的样本」,不一定是真实错误的样本,这是一种基于不确定估计的选择方法。
02
置信学习开源工具:cleanlab
pip install cleanlab
使用,具体文档说明在这里cleanlab文档说明。
from cleanlab.pruning import get_noise_indices
# 输入
# s:噪声标签
# psx: n x m 的预测概率概率,通过交叉验证获得
ordered_label_errors = get_noise_indices(
s=numpy_array_of_noisy_labels,
psx=numpy_array_of_predicted_probabilities,
sorted_index_method='normalized_margin', # Orders label errors
)我们来看看cleanlab在MINIST数据集中找出的错误样本吧,是不是感觉很牛~

如果你不只是想找到错误标注的样本,还想把这些标注噪音clean掉之后重新继续学习,那3行codes也可以搞定,这时候连交叉验证都省了~:
from cleanlab.classification import LearningWithNoisyLabels
from sklearn.linear_model import LogisticRegression
# 其实可以封装任意一个你自定义的模型.
lnl = LearningWithNoisyLabels(clf=LogisticRegression())
lnl.fit(X=X_train_data, s=train_noisy_labels)
# 对真实世界进行验证.
predicted_test_labels = lnl.predict(X_test)笔者注:上面虽然只给出了CV领域的例子,但置信学习也适用于NLP啊~此外, cleanlab可以封装任意一个你自定义的模型,以下机器学习框架都适用:scikit-learn, PyTorch, TensorFlow, FastText。
03
置信学习的3个步骤
cleanlab
操作起来比较容易,但置信学习背后也是有着充分的理论支持的。事实上,一个完整的置信学习框架,需要完成以下三个步骤 ( 如图1所示 ):
Count:估计噪声标签和真实标签的联合分布;
Clean:找出并过滤掉错误样本;
Re-Training:过滤错误样本后,重新调整样本类别权重,重新训练;
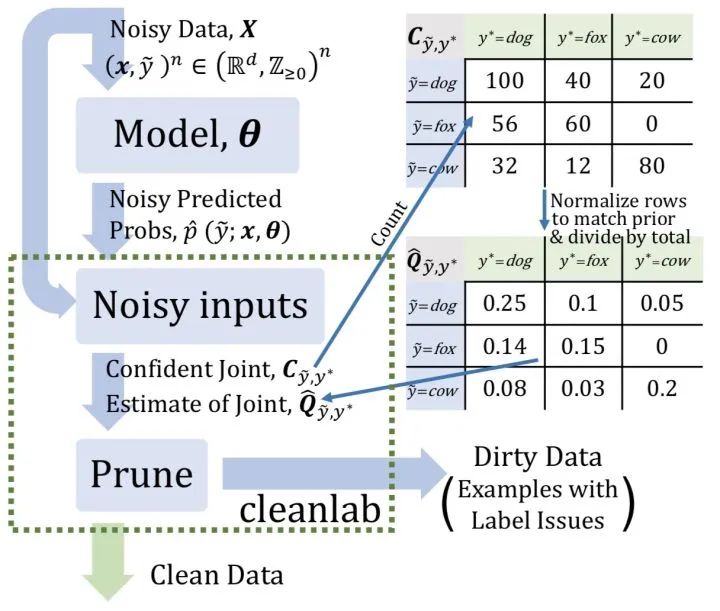
下面对上述3个步骤进行详细阐述:
1. Count:估计噪声标签和真实标签的联合分布
我们定义噪声标签为 



为了估计联合分布,共需要4步:
step 1 : 交叉验证
首先需要通过对数据集集进行交叉验证计算第
样本在第
个类别下的概率
;
然后计算每个人工标定类别
下的平均概率
作为置信度阈值;
最后对于样本
,其真实标签
为
个类别中的最大概率
,并且
;
step 2:
计算计数矩阵 

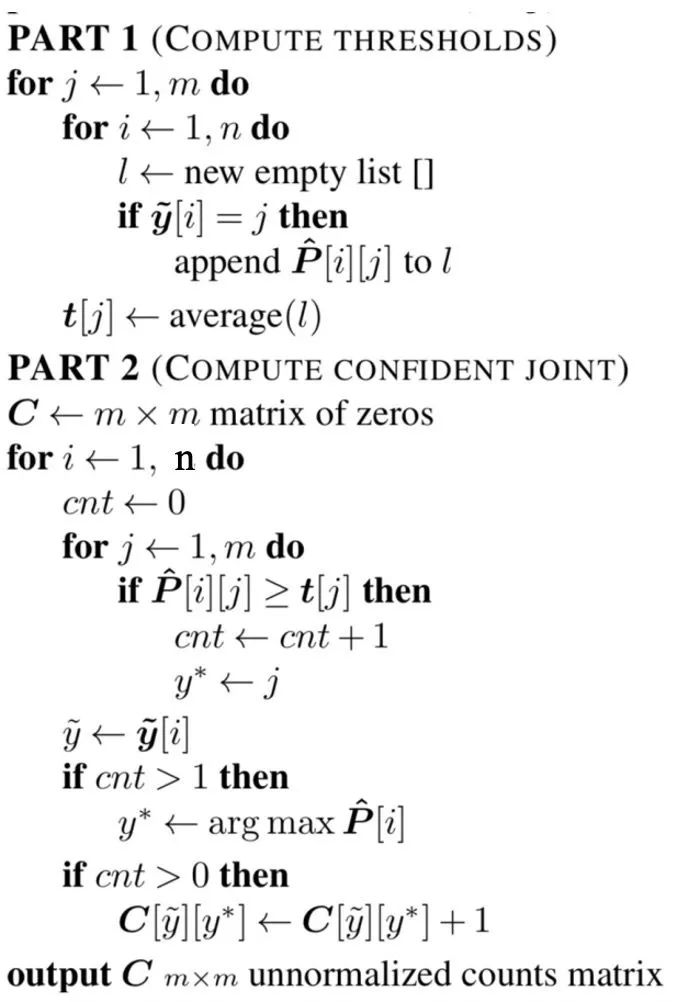
图2 计数矩阵C计算流程
step 3 : 标定计数矩阵
目的就是为了让计数总和与人工标记的样本总数相同。计算公式如下面所示,其中 


step 4 :
估计噪声标签



看到这里,也许你会问为什么要估计这个联合分布呢?其实这主要是为了下一步方便我们去clean噪声数据。此外,这个联合分布其实能充分反映真实世界中噪声 ( 错误 ) 标签和真实标签的分布,随着数据规模的扩大,这种估计方法与真实分布越接近 ( 原论文中有着严谨的证明,由于公式推导繁杂这里不再赘述,有兴趣的同学可以详细阅读原文~,后文的图7也有相关实验进行证明 )。
看到这里,也许你还感觉公式好麻烦,那下面我们通过一个具体的例子来展示上述计算过程:
step 1 : 通过交叉验证获取第 





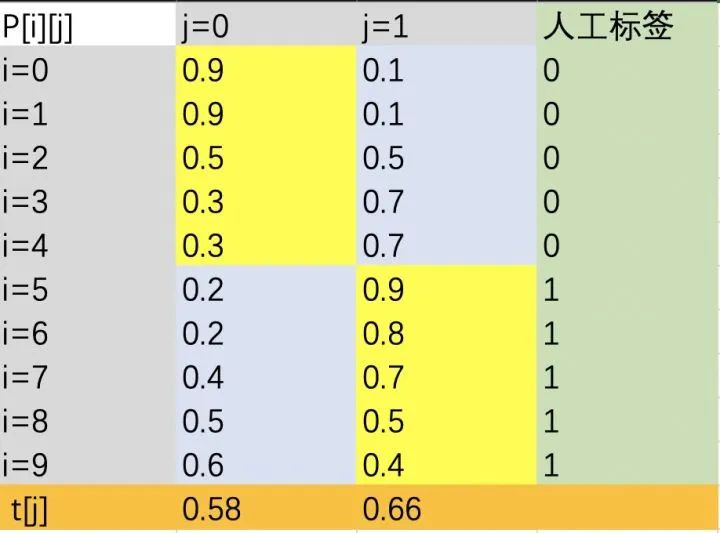
图3 P[i][j]和t[j]计算
step2:根据图2的计算流程,我们得到计数矩阵 

step3:标定后的计数矩阵 



step4:联合分布 
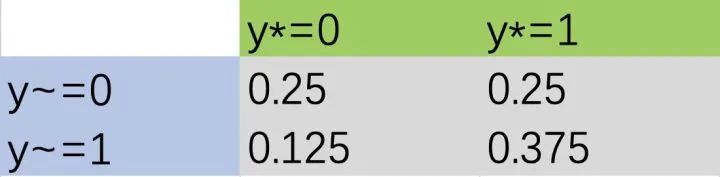
图5 联合分布Q计算
2. Clean:找出并过滤掉错误样本
在得到噪声标签和真实标签的联合分布 
Method 1:



Method 2:

Method 3:Prune by Class ( PBC ),即对于人工标记的每一个类别 


Method 4:Prune by Noise Rate ( PBNR ),对于计数矩阵 


Method 5:C+NR,同时采用Method 3和Method 4。
我们仍然以图3给出的示例进行说明:
Method 1:过滤掉i=2,3,4,8,9共5个样本;
Method 2:进入到计数矩阵非对角单元的样本分别为i=3,4,9,将这3个样本过滤;
Method 3:对于类别0,选取 

Method 4:对于非对角单元 

cleanlab
也有提供,我们只要提供2个输入、1行code即可clean错误样本:
import cleanlab
# 输入
# s:噪声标签
# psx: n x m 的预测概率概率,通过交叉验证获得
# Method 3:Prune by Class (PBC)
baseline_cl_pbc = cleanlab.pruning.get_noise_indices(s, psx, prune_method='prune_by_class',n_jobs=1)
# Method 4:Prune by Noise Rate (PBNR)
baseline_cl_pbnr = cleanlab.pruning.get_noise_indices(s, psx, prune_method='prune_by_noise_rate',n_jobs=1)
# Method 5:C+NR
baseline_cl_both = cleanlab.pruning.get_noise_indices(s, psx, prune_method='both',n_jobs=1)3. Re-Training:过滤错误样本后,重新训练
在过滤掉错误样本后,根据联合分布 


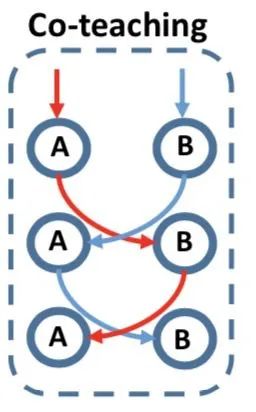
图6 Co-teaching
如图6所示,Co-teaching的基本假设是认为noisy label的loss要比clean label的要大,于是它并行地训练了两个神经网络A和B,在每一个Mini-batch训练的过程中,每一个神经网络把它认为loss比较小的样本,送给它其另外一个网络,这样不断进行迭代训练。
04
实验结果
上面我们介绍完成置信学习的3个步骤,本小节我们来看看这种置信学习框架在实践中效果如何?在正式介绍之前,我们首先对稀疏率进行定义:稀疏率为联合分布矩阵、非对角单元中0所占的比率,这意味着真实世界中,总有一些样本不会被轻易错标为某些类别,如老虎图片不会被轻易错标为汽车。
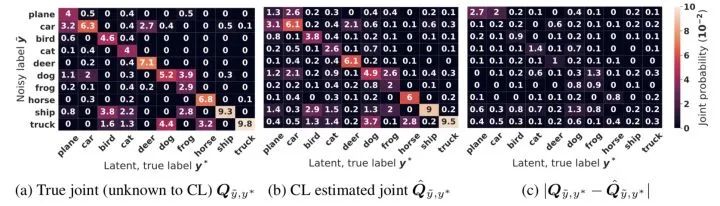
图7 真实联合分布和估计联合分布
图7给出了CIFAR-10中,噪声率为40%和稀疏率为60%情况下,真实联合分布和估计联合分布之间的比较,可以看出二者之间很接近,可见论文提出的置信学习框架用来估计联合分布的有效性。
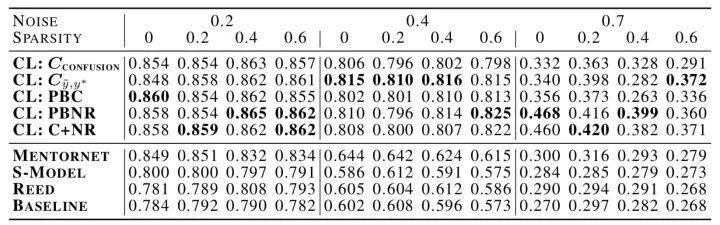
图8 不同置信学习方法的比较
上图给出了CIFAR-10中不同噪声情况和稀疏性情况下,置信学习与其他SOTA方法的比较。例如在40%的噪声率下,置信学习比之前SOTA方法Mentornet的准确率平均提高34%。
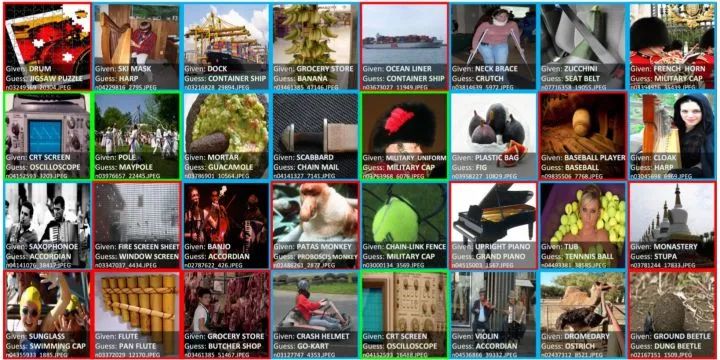
论文还将提出置信学习框架应用于真实世界的ImageNet数据集,利用CL:PBNR找出的TOP32标签问题如图9所示,置信学习除了可以找出标注错误的样本 ( 红色部分 ),也可以发现多标签问题 ( 蓝色部分,图像可以有多个标签 ),以及本体论问题:绿色部分,包括"是" ( 比如:将浴缸标记为桶 ) 或"有" ( 比如:示波器标记为CRT屏幕 ) 两种关系。
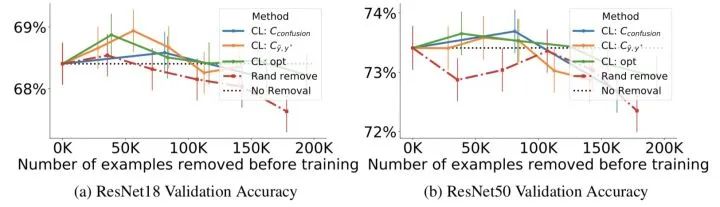
图10给出了分别去除20%,40%…,100%估计错误标注的样本后训练的准确性,最多移除200K个样本。可以看出,当移除小于100K个训练样本时,置信学习框架使得准确率明显提升,并优于随机去除。
05
总结
本文介绍了一种用来刻画noisy label、找出错误标注样本的方法——置信学习,是弱监督学习和带噪学习的一个分支。
置信学习直接估计噪声标签和真实标签的联合分布,而不是修复噪声标签或者修改损失权重。
cleanlab
可以很快速的帮你找出那些错误样本!可在分钟级别之内找出错误标注的样本。
接下来,让我们尝试将置信学习应用于自己的项目,找出那些“可恶”的数据噪声吧~
今天的分享就到这里,谢谢大家。
[1] Confident Learning: Estimating Uncertainty in Dataset Labels
[2] Co-teaching: Robust Training of Deep Neural Networks with Extremely Noisy Labels
原文链接:
https://zhuanlan.zhihu.com/p/146557232
作者介绍:
娄杰,毕业于北京理工大学,现就职于零氪智能科技 ( LinkDoc ),研究方向为:信息抽取、知识图谱与自然语言处理。
在文末分享、点赞、在看,给个三连击呗~~
社群推荐:

关于我们:
🧐分享、点赞、在看,给个三连击呗!👇