ICLR 2020 | reformer高效处理长序列,单机能跑,计算资源贫困人士的福音
背景
机构:Google Research 、U.C. Berkeley
作者:Nikita Kitaev、Łukasz Kaiser、Anselm Levskaya
论文地址:
https://www.aminer.cn/pub/5e5e189993d709897ce1ddbc
收录会议:ICLR2020
论文代码:
https://github.com/google/trax/tree/master/trax/models/reformer
基于 Transformer 的各种巨型模型在各种自然语言处理任务中常常能够取得最优结果,但这些模型的训练成本往往过高,在针对长序列文本上尤甚。为此,本文提出两种技术以改善基于 Transformer 的这类模型,名为 Reformer。第一,使用局部敏感 hash,替换原始的点乘方式的 attention,从而将其空间复杂度从 O(L^2)降低到O(Llog L),其中L表示文本序列的长度。第二,使用逆残差层代替标准的残差,这使得训练过程中只需存储一次激活值,而无需 N 次,其中 N 表示网络层数。最终的结果表明 Reformer 性能与 Transformer 相当,同时在长序列上具有更高的内存效率和更快的速度。
那训练 Transformer 模型是否真需要很多资源且很低效?以现有的最大 Transformer 层为例,该 Transformer 层中参数量是 0.5B,这需要 2GB 的内存。(1M=1024KB,1KB=1024Byte。所以1GB=1024M=1024x1024KB=1024x1024x1024Byte=1073741824Byte。float 占用 4 个 Byte。0.5B 即 5 亿参数,需要的内存量为 5 亿 *4 字节=20 亿字节。这差不多是 1.86GB 即约为 2GB)对于由 64Ktokens 组成的序列,如果嵌入层的尺寸是 1024,batch size 是 8,那么激活值需要 64K * 1K * 8=0.5B 个浮点数来存储,这又需要 2GB 的内存。如果每层的内存占用只有上述提到的这些的话,那么在单加速器上使用Transformer 处理 64K长度的序列也是轻而易举。此外,如此前提下训练 BERT 的整个语料库也只需 17GB 的内存。然而,现实并非如此,真实环境下为何甚至不能在单台机器上对这些模型进行微调呢?
这是因为上述仅仅考虑单层参数的内存占用和输入激活值的内存消耗,而忽略了 Transformer 在内存占用上的主要问题:
- 需要存储激活值用于反向传播,那么 N 层模型内存占用是单层的 N 倍;
- 由于中间全连接层的深度 d_{ff} 通常远大于注意力激活层的深度 d_{model},而这需要占用很大的内存;
- 长度为 L 的序列的 attention 的时间和空间复杂度是 O(L^2),那么对于 64K tokens 的序列就会耗尽内存。
为此,本文提出 Reformer 模型以解决上述问题,具体采用如下方案:
- 可逆层(Reversible layer),在整个模型中只使用单个副本,可以消除层数因子 N。
- 前馈层(feed-forward layer)分开激活和分块处理,从而消除 d_{ff} 因子的影响,降低前馈层的内存占用。
- 采用基于局部敏感哈希(locality-sensitive hashing,LSH)的近似注意力计算,让注意力层的 O(L^2) 因子变为 O(L log L) ,这使得在长序列上的处理成为可能。
局部敏感哈希 ATTENTION
点乘 attention:
标准的 Transformer 使用点乘的 attention,queries 和 keys 的维度都是 d_k,values 的维度是 d_v。query 先与 key 做点乘,再除以根号 d_k,再输入到 softmax 中得到 value 的权重,最后权重再与 value 相乘,得到最终的结果。在实际操作过程中是以矩阵方式进行批量操作,queries 组成矩阵 Q,keys 组成矩阵 K,values 组成矩阵 V,上述流程概况如下:
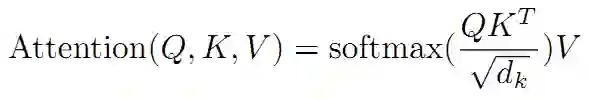
多头 attention:
上述的 attention 操作并行地进行 h 次,再输出维度为 d_v 的输出结果。再将这些结果拼接,再做一次投射操作得到最终的结果。即所谓的多头 attention。
高效内存 attention:
先来算下上述 attention 机制消耗的内存。假设 Q,K,V 的尺寸为 [batch_size,length,d_model]。QK^T 的尺寸为 [batch_size,length,length]。当 length=64k,即使 batch_size=1,那么 64k*64k 大小的矩阵,如果用 32 位浮点数来存储的话,需要 16GB 内存。鉴于此,在长序列上使用 Transformer 显得不切实际。但是需要注意的是,QK^T 矩阵可以不必全部放在内存中,可以对每个 query 分别计算 attention。反向传播计算梯度时再重新计算一次。这种方式计算 attention 虽然低效,但是所占用的内存与 length 成正比。这种方法在本文这里作为一种全 attention 的 baseline。
Q,K,V 从何处来?
上述讨论了 Q、K、V,但是一般我们只会得到大小为 [batch_size,length,d_model] 的激活值 A,这些值是 token 的嵌入所组成的句向量。那么为了从 A 中得到Q、K、V,Transformer 使用了 3 个不同的线性层(参数不同)将 A 投射为 Q、K、V。对于使用局部敏感哈希 attention 的模型,我们希望 queries 和 keys(即 Q 和 K)相同。只需要 A 投射到 Q 和 A 投射到 K 时采用相同线性变换参数即可,而 A 投射到 V 时采用不同参数。这种方式成为共享 QK-Transformer。实验表明共享 QK 并不会影响 Transformer 的性能,即使添加一项 d_k 的归一化项。
Hashing attention:
在 LSH attention 中,假设 Q、K、V 的尺寸为 [batch_size,length,d_model],同时仍然使用此前介绍的多头 attention 机制。那么 QK^T 的尺寸为 [batch_size,length,length]。由于 softmax(QK^T) 的计算结果主要取决于值最大的部分,对于每个 query 只需关注 K 中与 query 最接近的点。当 K 的长度是 64k,那么对个每个 query,本文仅仅考虑其最近的的 32 或 64 个 keys。如此会更加高效,那么如何找寻最近的那些 keys 呢?
局部敏感哈希(LSH):
在高纬空间中找寻最近邻可以使用局部敏感哈希(LSH)。将每个向量 x 通过 hash 函数h(x) 进行映射,如果近处的向量获得相同的 hash,且具有高概率,而远处的向量没有,那么这样的 hash 称为位置敏感型 hash。在此处例子中,我们实际上只要求近邻的向量以高概率具有相同的 hash 值,并且 hash 桶也以高概率具有相同的大小。
具体是使用如 Figure 1 所示的随机投射方法:
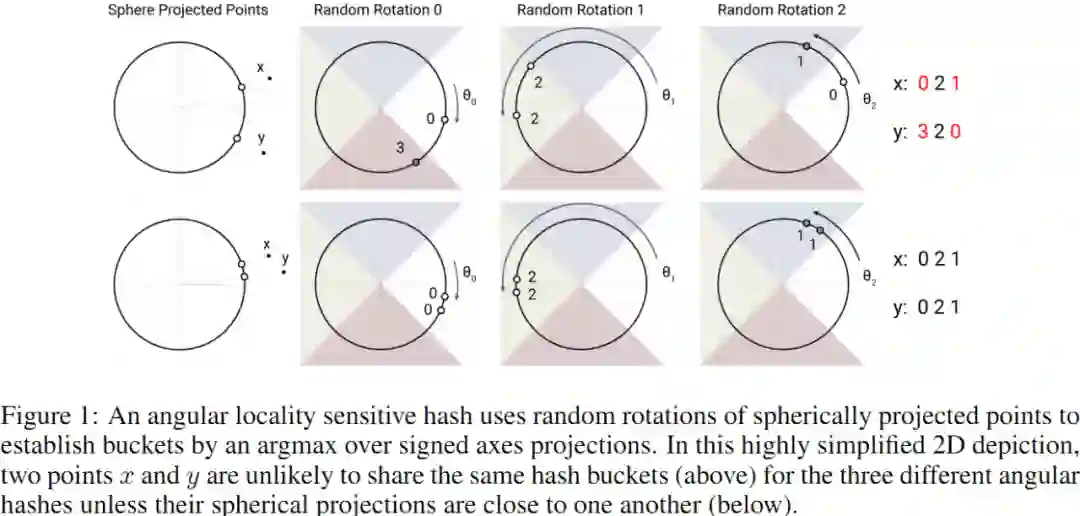
图片来源:https://towardsdatascience.com/illustrating-the-reformer-393575ac6ba0
这里有两个点,它们投影到一个单位圆上,并以不同的角度随机旋转 3 次。可以观察到,它们不太可能共享同一个 hash 桶。在后续例子中,可以看到两个非常接近的点在3 次随机旋转后会位于相同的 hash 桶:
https://miro.medium.com/max/1052/1*aArg6a26KqbIlEkT43fxlw.gifAngular LSH 最近邻搜索的的一个简化动画:两个点很接近的情况。
图片来源:https://towardsdatascience.com/illustrating-the-reformer-393575ac6ba0
LSH attention:
综合考虑上述的 LSH 策略和 hashing attention,先重写单个 query 在位置 i 的常规 attention:

其中 P_i 表示 query 在位置 i 所需要 attend 的集合,z 表示配分函数(partition function)比如 softmax 中的归一化项。为了书写清楚,这里省略了缩放项根号 d_k。
对于批量操作,当遮蔽掉不在 P_i 中的元素,此时常规 attention 定义如下:

即对于不能 attend 到的位置,m(j, P_i) 为正无穷,那么 q_i* k_j 减去正无穷再去 exp 操作,其结果为 0。这样就不需要对于每个位置i都有单独的 P_i。
在 LSH attention 中,query 中位置 i 所能够 attend 的限制集合 P_i 被限制到一个 hash 桶中。Figure 2(a-b)展示的是全 attention 和 hash attention 的对比。
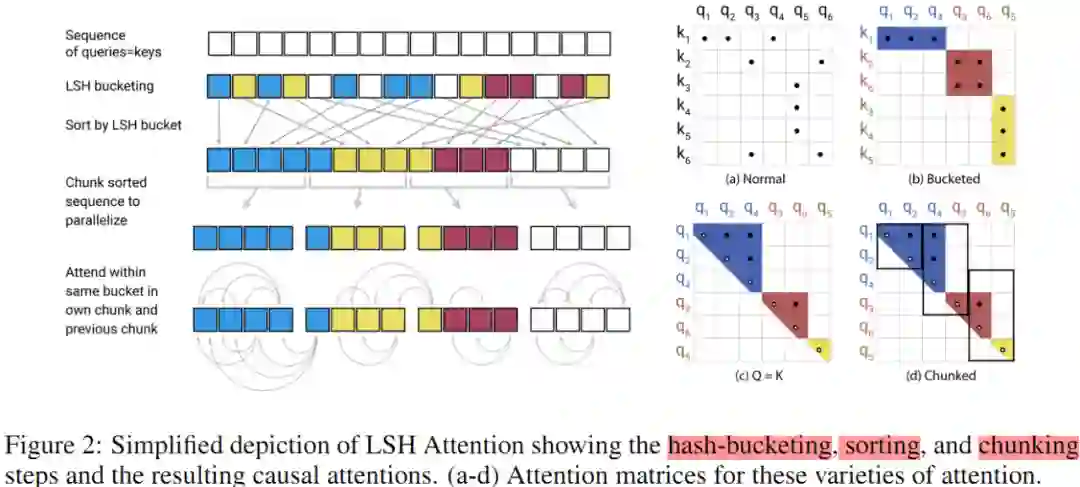
图 b:计算 query 和 key 所归属的 hash 桶。再按照桶进行排序,同一个桶又按照原本的位置进行排序得到图 b。可以看到,同一个桶,可以出现多个 query 但 keys 很少的情况,例如图中蓝色的桶 query 有 3 个,都 attend 到同一个 key 中。由于相似的 item 很有可能落在同一个桶里,所以只在每个桶内部进行 attention 就可以近似全 attention。
图 c:为了缓解桶中 q 和 k 不均衡问题,本文通过令 $k_{j}=\frac{q_{j}}{\left\|q_{j}\right\|}$ 使得 h(k_j)=h(q_j),即使用了 share-QK attention。然后先按照桶序号对 queries 排序,每个桶中,仍按照原本的 position 位置大小排序。得到图 c。对比 b 图和 c 图可以看出,纵轴的 k 已经变成了 q。这时就能保证对角线都是 attend 到的而且 q 和 k 在桶中的个数一样(因为 Q=K)。排序后的 attention 矩阵,相同桶的值会在对角线附近聚集。注意到图中对角线的点为空心,这是因为虽然在正常情况下,q 会 attend to 本身位置的 value,但是在 share-QK 的实现下,如果 attend to 本身,会导致其值特别大,其他的值特别小,经过 softmax 之后,其他都是 0,就自己本身是 1。所以为了避免这种情况,q 不会去 attend 自身位置的值,除非只有自己本身可以 attend。
图 d:即使 Q=K,还是会出现一个问题:有的桶中个数多,有的桶中个数少。比如一个极端情况,2 个桶,其中一个桶占据了所有的 keys,另一个桶为空,那么 LSH attention 就没有起作用。于是在图 c 的基础上,增加了 chunk 的操作。对输入进行排序之后(即图 c 中先桶排序,同个桶内按照 token 的 position 排序)得到新的序列顺序 s_i,比如图中原来的序列顺序是 [q_1,q_2,q_3,q_4,q_5,q_6],新的序列顺序是[q_1,q_2,q_4,q_3,q_6,q_5] 。每个 chunk 内 query 的上限个数为 $m=\frac{2 l}{n_{\text {buckets}}}$, (l 为输入 query 的长度) ,每个桶平均大小为 $m=\frac{l}{n_{\text {buckets}}}$,这里假设桶中数量增加到均值两倍的概率足够低。对于桶中的每个 query,都可以 attend to 自己以及前一个桶中相同 hash 值的 key。
小结下,LSH attention 做了以下两个事情:
第一,找到 Q、K 矩阵的 LSH hashes。
第二,在同一个 hash 桶内计算 k 和 q 向量的标准 attention。
更具体来说可分为以下 5 个步骤:
第一,令输入序列 queries=keys
第二,做 LSH bucketing,即进行 hash 计算,得到每个 query 和 key 所归属的桶(不同颜色表示不同的桶)。
第三,根据桶编号对 query 进行排序,同个桶中,按照 query 原本的位置进行排序。
第四,对于排序后的新序列,进行 chunk 拆分
第五,对于每个 query 只 attend 自己以及自己之前的 chunk,对于这些候选集中相同桶的 key 进行 attend。
多轮 LSH attention:
LSH 有近似性,即不能保证相似的输入能在同一个桶中。为了减轻这个问题,采用了 multi-round LSH attention。即重复上述过程多次,以使类似的 item 以尽可能高的概率落入相同的桶中,尽量避免相似 item 落入不同桶。更多的细节参考附件 A。
可逆层
如上所述,attention 的复杂度可以被减少为与序列长度成线性正比,但是,参数量占的复杂度依旧很高,如何进一步减少呢?这里就开始尝试解决前文介绍部分所提到的第二和第三个问题,即大量的 encoder 和 decoder 层、全连接层 FFN 的深度问题。
Reversible residual Network (RevNet)
RevNet 的思想是每一层的 activations 可以根据下一层的 activations 推导获得,从而不需要在内存中储存 activations。在原本的 residual layer 中,由公式 y=x+F(x) 输出得到 activations。其中 F 是 residual 函数。在 RevNet 中,先将输入x分为两个部分 x_1 和 x_2,然后通过不同 residual functions:F() 和 G() 得到输出 y_1 和 y_2:


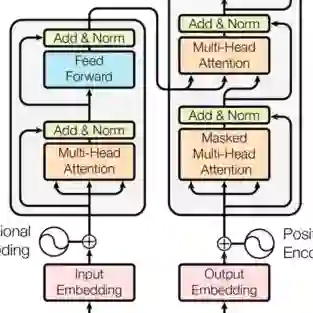
那么如何在 Transformer 中引入 RevNet?将 attention layer 和 FFN layer 通过 ResNet 连接,从而减少内存的消耗。具体是令F函数为 attention 层,G 函数作为 FFN 层。需要注意的一点是 layer normalization 是包含在 residual blocks 中的。

Chunking
上述消除了 n_l 项的影响,深层的网络仍然占有大量内存。在 FFN 中中间隐藏层的纬度通常非常大,比如 d_{ff}=4k 或者更大。由于 FFN 的计算与序列中的位置完全无关,因此计算可以被分割成 c 个块,以降低内存的使用。虽然该操作其实可并行处理,但是每次只计算一个 chunk,通过时间换取内存空间。

可逆层和共享 query-key 的影响:
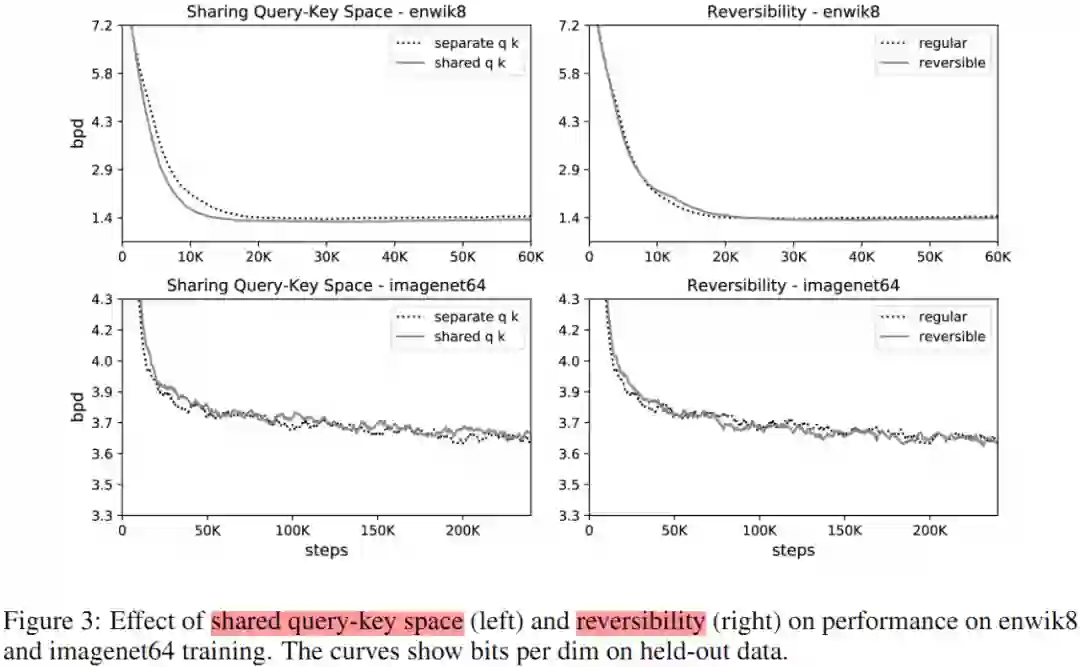
Figure 3 中的右部分验证的是可逆层的影响。实验中对比的可逆层和常规 Transformer 参数量相同,且学习曲线看起来也几乎相同。这些结果表明,可逆 Transformer 在节省内存的同时并不会牺牲精度。
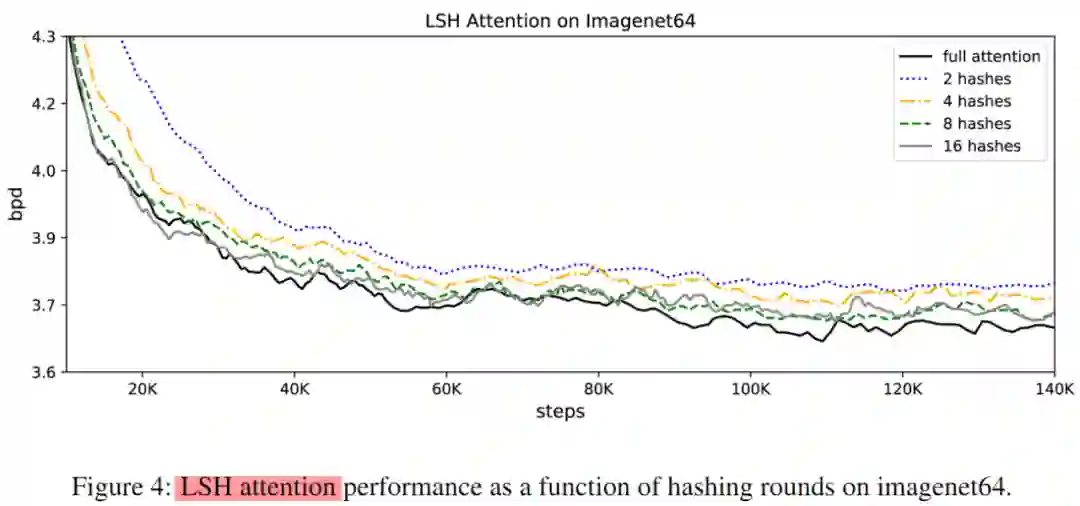
LSH attention 的影响:
如 Figure 4 所示,可以看出随着 hash 数的增多精度也提升了。
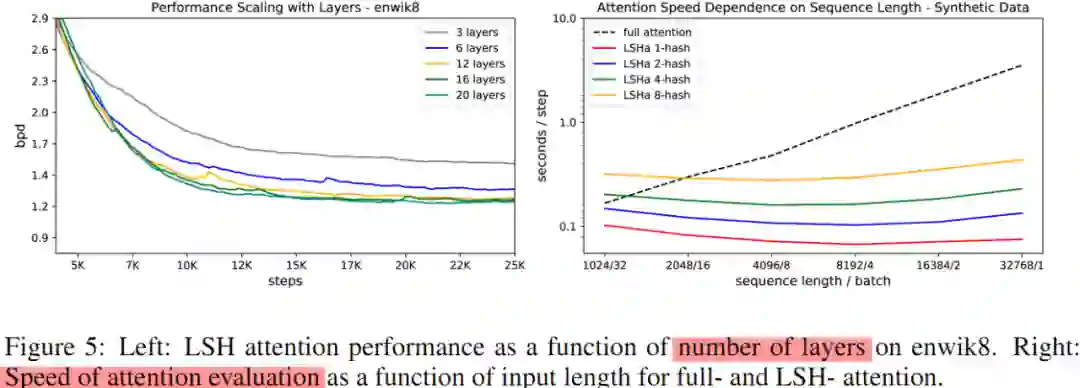
更大的 Reformer 模型:
Figure 5 展示了不同层数的 Reformer 在 envik8 和 imagenet64 上的表现。下图(左)是 Big Reformer 随层数变化指标结果,20 层依然无压力。而下图(右)是普通 attention 和 LSH attention 在不同序列长度的速度比较,当序列很长的时候,LSH 具有显著的优势。
作者:刘杰鹏(微信号:onepieceand)
毕业院校:华中科技大学
研究方向:机器阅读理解、文本生成等。
近期精彩集锦(点击蓝色字体跳转阅读):

点击阅读原文,查看更多精彩!