为什么要考虑函数的可微性? - 简单微积分

让我们放松下来，

轻松地去探索

微积分的本质吧！

下文节选自《简单微积分》, 已获人邮图灵授权许可, [遇见数学] 特此表示感谢! 

微积分的真身

     微分的可能性

对于高中或者大学教材中的一些内容，一些学习者会产生这样的疑问：“这种理所当然的事情，为何还有学习的必要？”

这类内容其实比较难理解其意义，“可微性”就是其中一例。可微性在高中显露头角，到大学则会频繁出现。例如下面这个，

在原点不可微分。

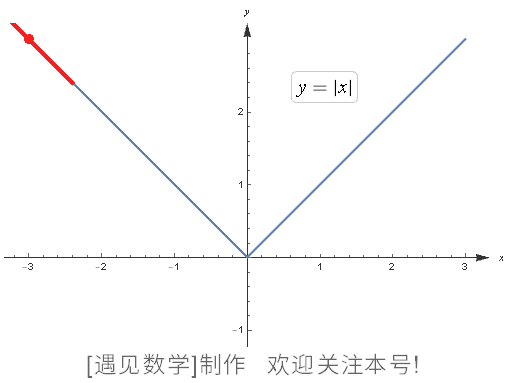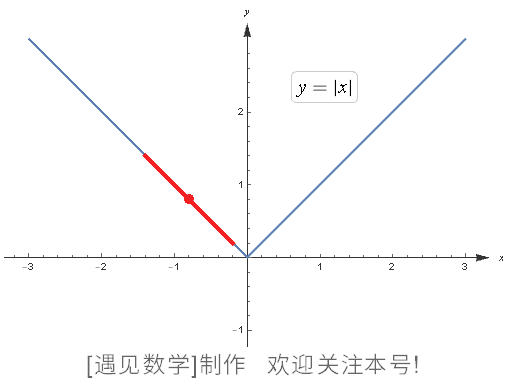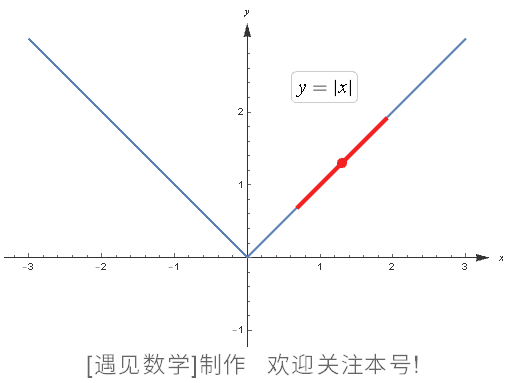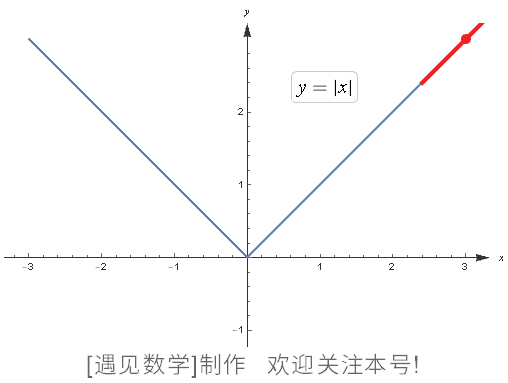
图124　不可微函数的例子

或许有些读者并不了解，曲线顺滑（可以微分的）函数，它的极限也不一定可以微分。

这是比较专业的内容了，在这里简单地解释下。

图 125 表示的是“把顺滑的波按照一定规则，分别以 2 个（ n = 2 ）、3 个（ n = 3 ）、4 个（ n = 4 ）的形式合并出的图像”。右下方的函数是无限合并的波，叫作魏尔斯特拉斯函数。

合并的波在有限数量范围内是顺滑的，但是无限合并顺滑的波形成的魏尔斯特拉斯函数却在所有的点上都无法微分。

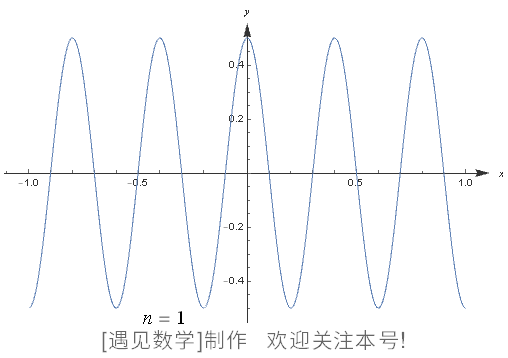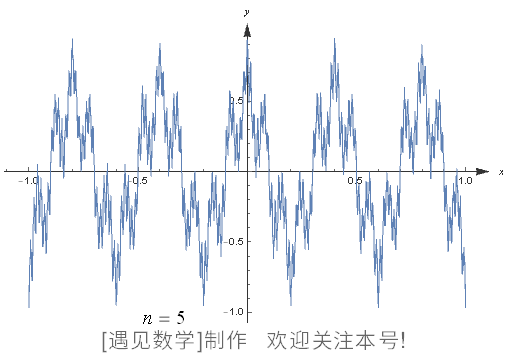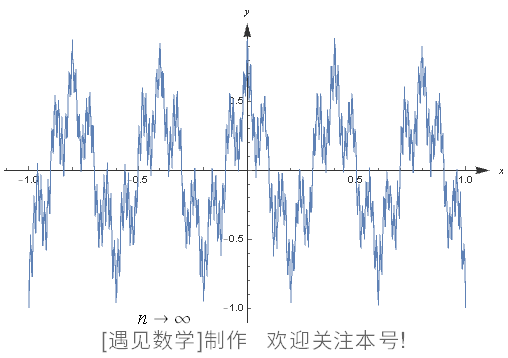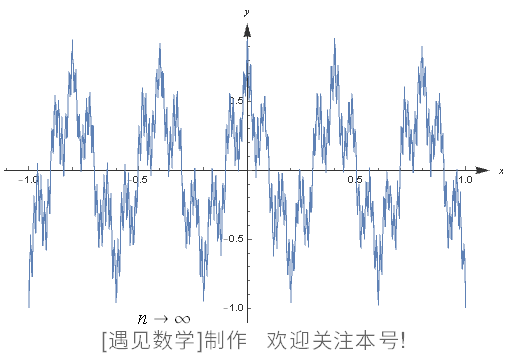
图125　直到形成魏尔斯特拉斯函数

因为存在这种例子，所以数学家每次说“可不可以微分” 时，都会让人神经敏感。比如说不可微函数，一般也很难计算其最大值。

这是因为，如果不可微分，就无法使用

微分 = 0

这个方程式，即任何位置都不可微的函数的图像都无限复杂。

即使从局部来看，不可微函数的图像也并不单纯，这一点和可微函数存在本质上的不同。

可能有人会认为，这种病态函数难道不是罕见的例子吗？但是，事实并非如此。像海岸线那种锯齿状且无法微分的例子，真是一点儿也不罕见。