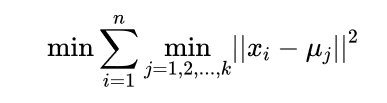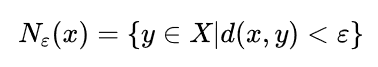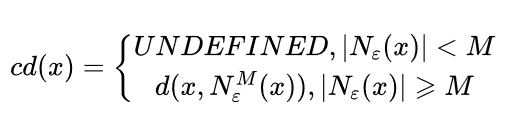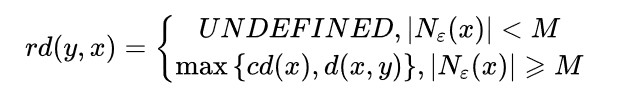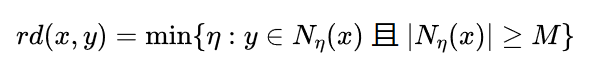为什么聚类技术依然是数据挖掘届的泰山北斗?
一、什么是聚类
1.1 聚类的定义
聚类(Clustering)是按照某个特定标准(如距离)把一个数据集分割成不同的类或簇,使得同一个簇内的数据对象的相似性尽可能大,同时不在同一个簇中的数据对象的差异性也尽可能地大。也即聚类后同一类的数据尽可能聚集到一起,不同类数据尽量分离。
1.2 聚类和分类的区别
-
聚类(Clustering):是指把相似的数据划分到一起,具体划分的时候并不关心这一类的标签,目标就是把相似的数据聚合到一起,聚类是一种无监督学习(Unsupervised Learning)方法。 -
分类(Classification):是把不同的数据划分开,其过程是通过训练数据集获得一个分类器,再通过分类器去预测未知数据,分类是一种监督学习(Supervised Learning)方法。
1.3 聚类的一般过程
-
数据准备:特征标准化和降维 -
特征选择:从最初的特征中选择最有效的特征,并将其存储在向量中 -
特征提取:通过对选择的特征进行转换形成新的突出特征 -
聚类:基于某种距离函数进行相似度度量,获取簇 -
聚类结果评估:分析聚类结果,如 距离误差和(SSE)等
1.4 数据对象间的相似度度量
对于数值型数据,可以使用下表中的相似度度量方法。
Minkowski距离就是
范数(
),而 Manhattan 距离、Euclidean距离、Chebyshev距离分别对应
时的情形。
1.5 cluster之间的相似度度量
除了需要衡量对象之间的距离之外,有些聚类算法(如层次聚类)还需要衡量cluster之间的距离 ,假设
和
为两个 cluster,则前四种方法定义的
和
之间的距离如下表所示:
-
Single-link定义两个cluster之间的距离为两个cluster之间距离最近的两个点之间的距离,这种方法会在聚类的过程中产生链式效应,即有可能会出现非常大的cluster -
Complete-link定义的是两个cluster之间的距离为两个``cluster之间距离最远的两个点之间的距离,这种方法可以避免链式效应`,对异常样本点(不符合数据集的整体分布的噪声点)却非常敏感,容易产生不合理的聚类 -
UPGMA正好是Single-link和Complete-link方法的折中,他定义两个cluster之间的距离为两个cluster之间所有点距离的平均值 -
最后一种 WPGMA方法计算的是两个cluster之间两个对象之间的距离的加权平均值,加权的目的是为了使两个cluster对距离的计算的影响在同一层次上,而不受cluster大小的影响,具体公式和采用的权重方案有关。
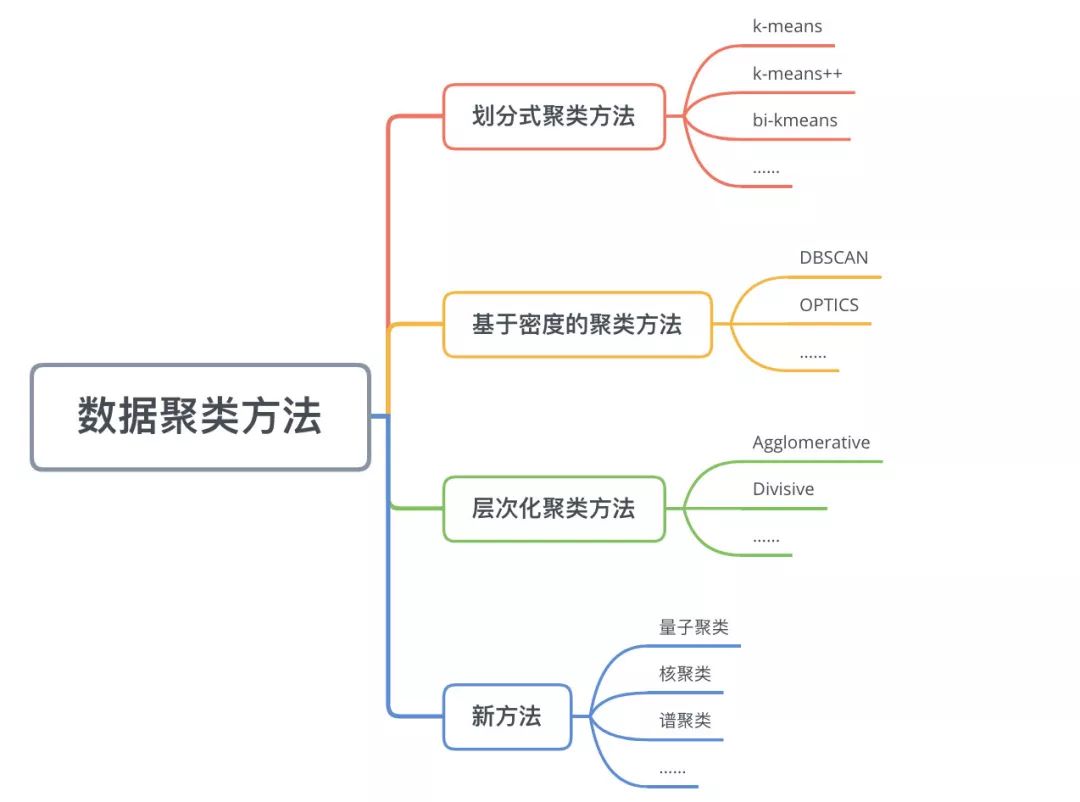
二、数据聚类方法
数据聚类方法主要可以分为划分式聚类方法(Partition-based Methods)、基于密度的聚类方法(Density-based methods)、层次化聚类方法(Hierarchical Methods)等。
2.1 划分式聚类方法
划分式聚类方法需要事先指定簇类的数目或者聚类中心,通过反复迭代,直至最后达到"簇内的点足够近,簇间的点足够远"的目标。经典的划分式聚类方法有k-means及其变体k-means++、bi-kmeans、kernel k-means等。
2.1.2 k-means算法
经典的k-means算法的流程如下:
创建 个点作为初始质心(通常是随机选择) 当任意一个点的簇分配结果发生改变时
对每个质心 将数据点分配到距其最近的簇 计算质心与数据点之间的距离 对数据集中的每个数据点 对每个簇,计算簇中所有点的均值并将均值作为质心
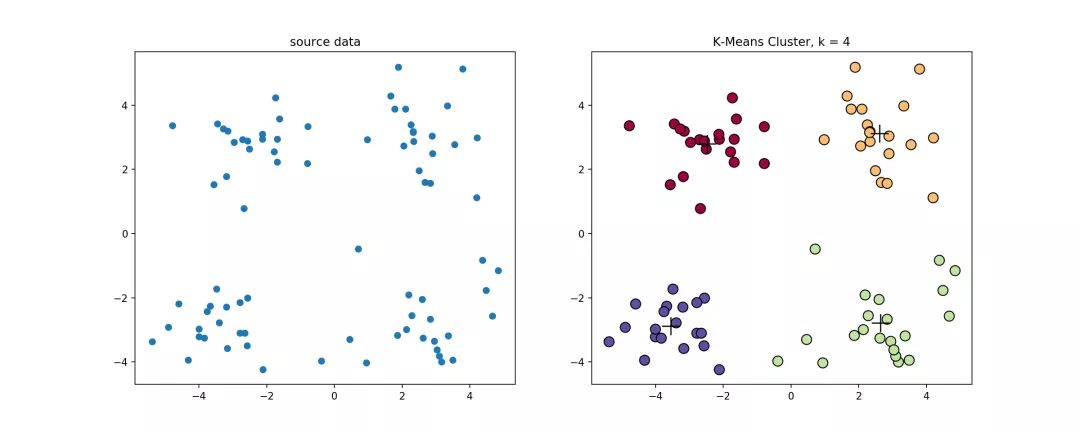
经典k-means源代码,下左图是原始数据集,通过观察发现大致可以分为4类,所以取
,测试数据效果如下右图所示。
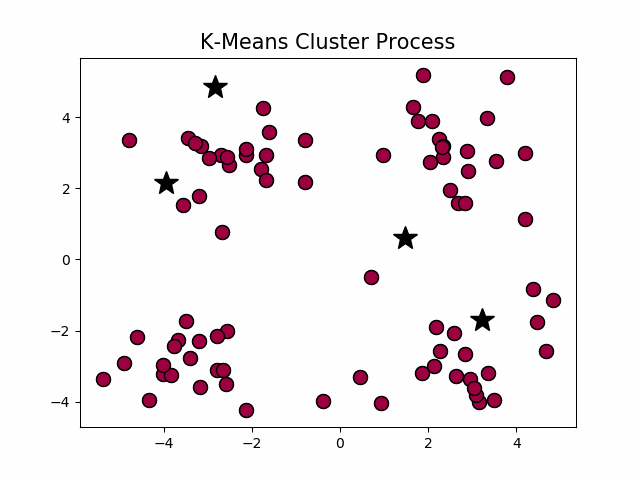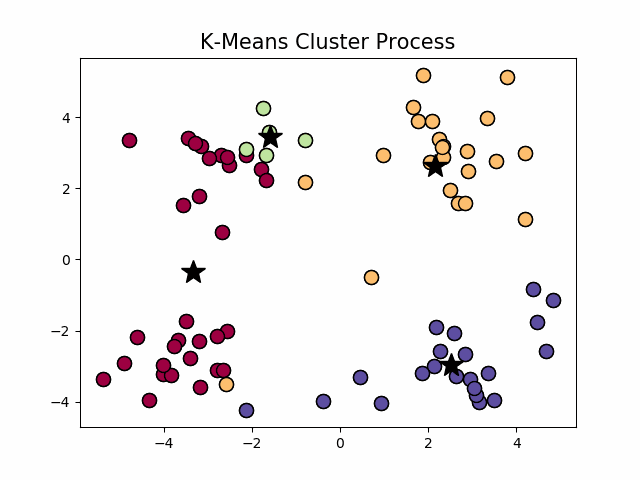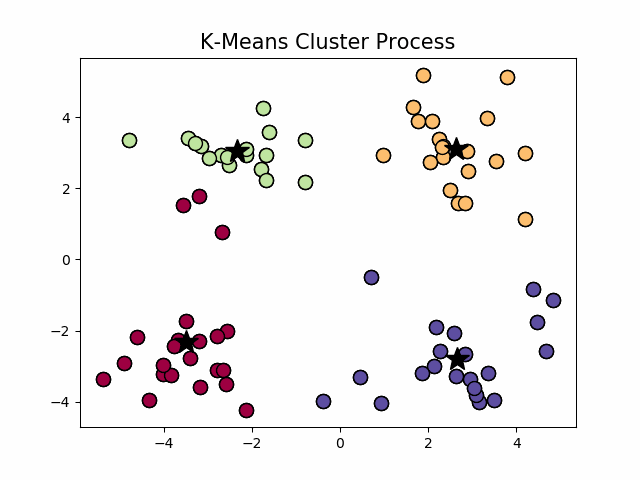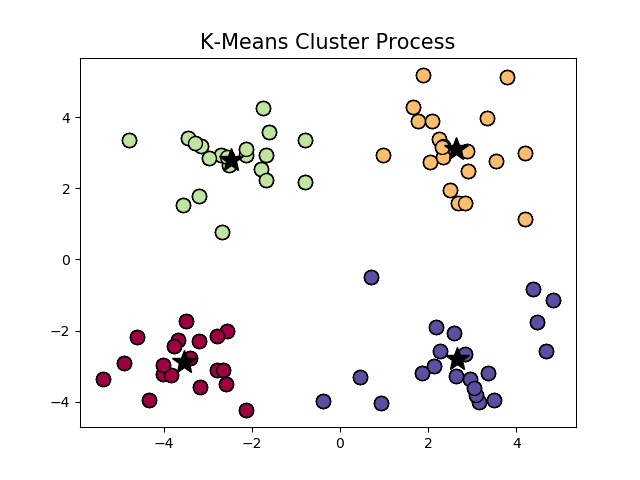
看起来很顺利,但事情并非如此,我们考虑k-means算法中最核心的部分,假设
是数据点,
是初始化的数据中心,那么我们的目标函数可以写成
这个函数是非凸优化函数,会收敛于局部最优解,可以参考证明过程。举个🌰, ,则
该函数的曲线如下图所示
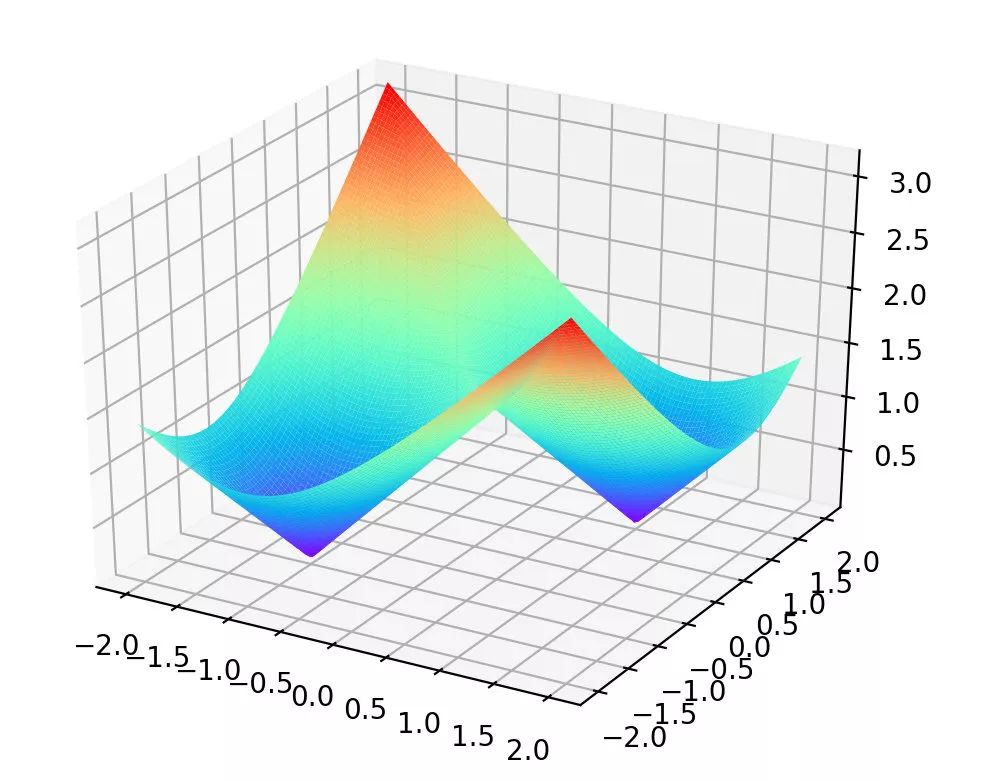
可以发现该函数有两个局部最优点,当时初始质心点取值不同的时候,最终的聚类效果也不一样,接下来我们看一个具体的实例。
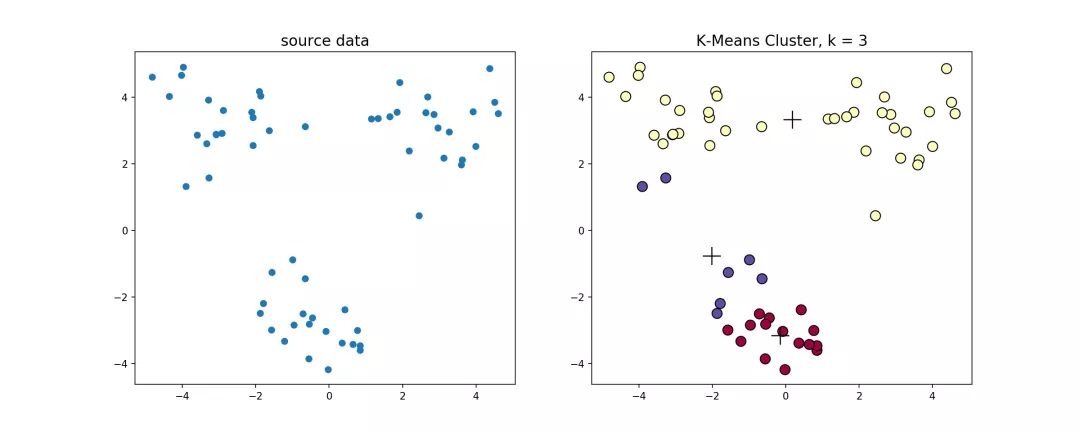
在这个例子当中,下方的数据应该归为一类,而上方的数据应该归为两类,这是由于初始质心点选取的不合理造成的误分。而 值的选取对结果的影响也非常大,同样取上图中数据集,取 ,可以得到下面的聚类结果:
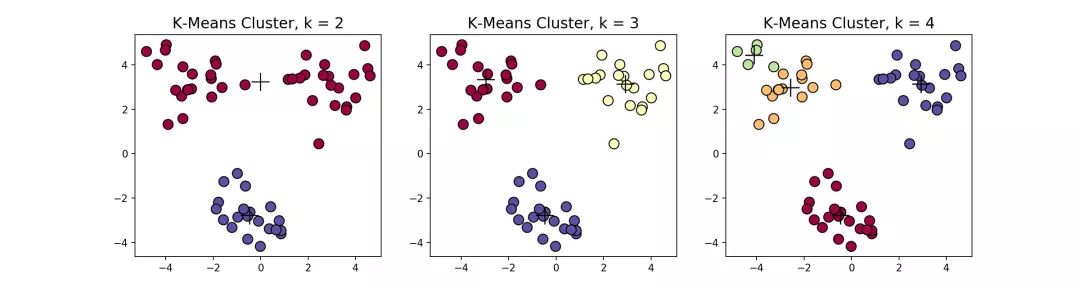
一般来说,经典k-means算法有以下几个特点:
-
需要提前确定 值 -
对初始质心点敏感 -
对异常数据敏感
2.1.2 k-means++算法
k-means++是针对k-means中初始质心点选取的优化算法。该算法的流程和k-means类似,改变的地方只有初始质心的选取,该部分的算法流程如下
随机选取一个数据点作为初始的聚类中心 当聚类中心数量小于
计算每个数据点与当前已有聚类中心的最短距离,用 表示,这个值越大,表示被选取为下一个聚类中心的概率越大,最后使用轮盘法选取下一个聚类中心
k-means++源代码,使用k-means++对上述数据做聚类处理,得到的结果如下
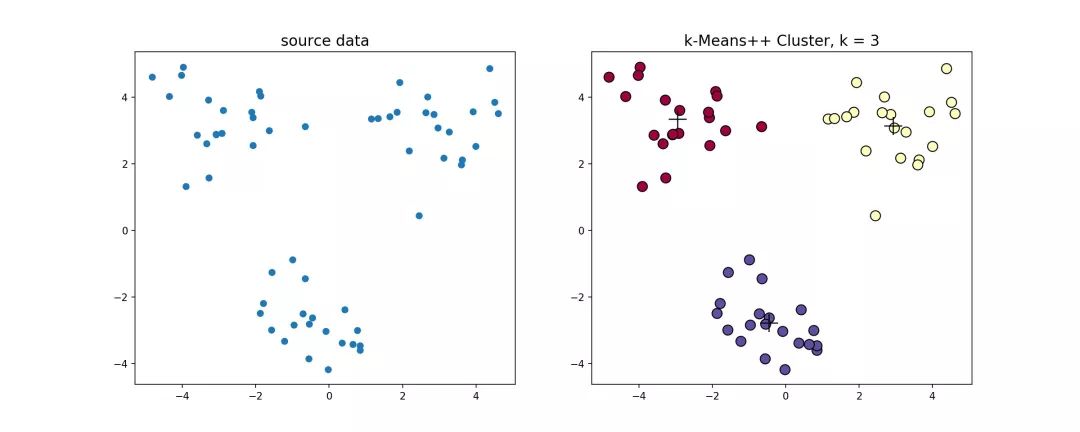
2.1.3 bi-kmeans算法
一种度量聚类效果的指标是SSE(Sum of Squared Error),他表示聚类后的簇离该簇的聚类中心的平方和,SSE越小,表示聚类效果越好。bi-kmeans是针对kmeans算法会陷入局部最优的缺陷进行的改进算法。该算法基于SSE最小化的原理,首先将所有的数据点视为一个簇,然后将该簇一分为二,之后选择其中一个簇继续进行划分,选择哪一个簇进行划分取决于对其划分是否能最大程度的降低SSE的值。
该算法的流程如下:
将所有点视为一个簇 当簇的个数小于 时
计算总误差 在给定的簇上面进行 k-means聚类( )计算将该簇一分为二之后的总误差 对每一个簇 选取使得误差最小的那个簇进行划分操作
bi-kmeans算法源代码,利用bi-kmeans算法处理上节中的数据得到的结果如下图所示。
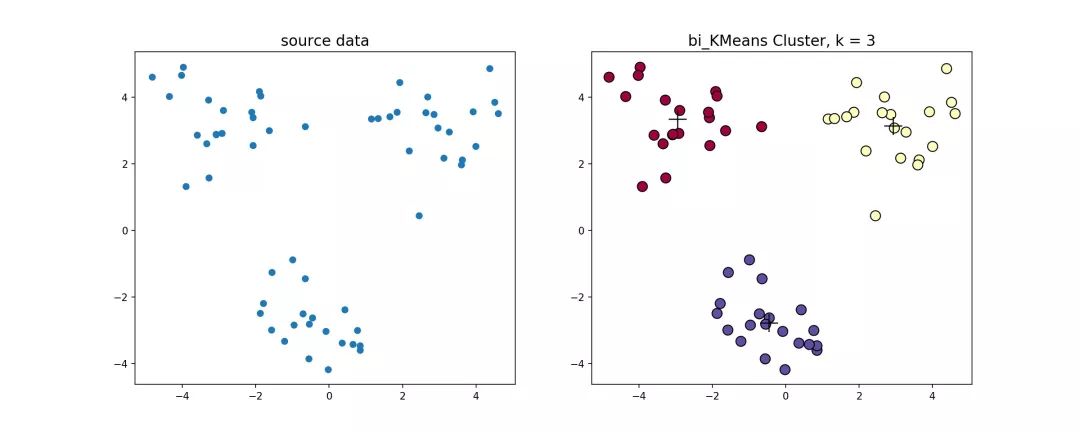
这是一个全局最优的方法,所以每次计算出来的SSE值肯定也是一样的,我们和前面的k-means、k-means++比较一下计算出来的SSE值
| 序号 | k-means | k-means++ | bi-kmeans |
|---|---|---|---|
| 1 | 2112 | 120 | 106 |
| 2 | 388 | 125 | 106 |
| 3 | 824 | 127 | 106 |
| agv | 1108 | 124 | 106 |
可以看到,k-means每次计算出来的SSE都较大且不太稳定,k-means++计算出来的SSE较稳定并且数值较小,而bi-kmeans每次计算出来的SSE都一样(因为是全局最优解)并且计算的SSE都较小,说明聚类的效果也最好。
2.2 基于密度的方法
k-means算法对于凸性数据具有良好的效果,能够根据距离来讲数据分为球状类的簇,但对于非凸形状的数据点,就无能为力了,当k-means算法在环形数据的聚类时,我们看看会发生什么情况。
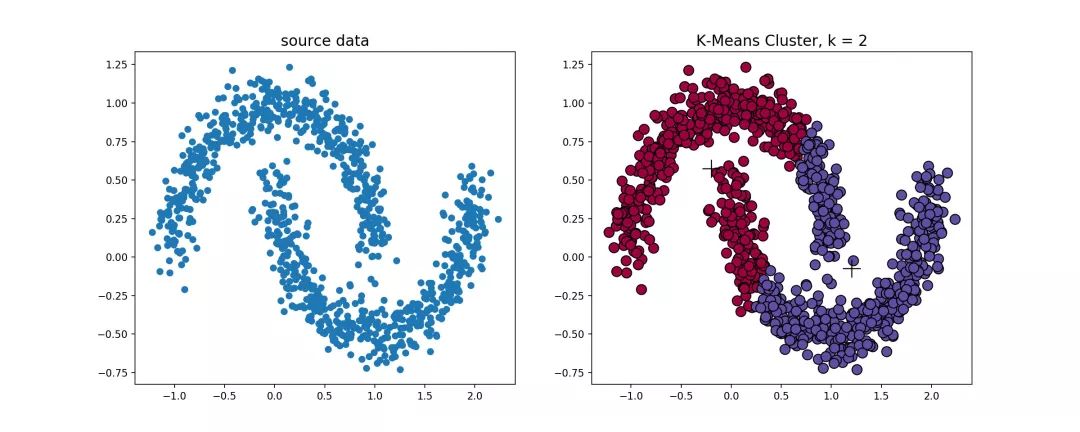
从上图可以看到,kmeans聚类产生了错误的结果,这个时候就需要用到基于密度的聚类方法了,该方法需要定义两个参数
和
,分别表示密度的邻域半径和邻域密度阈值。DBSCAN就是其中的典型。
2.2.1 DBSCAN算法
首先介绍几个概念,考虑集合 , 表示定义密度的邻域半径,设聚类的邻域密度阈值为 ,有以下定义:
-
邻域( -neighborhood)
-
密度(desity) 的密度为
-
核心点(core-point)
设 ,若 ,则称 为 的核心点,记 中所有核心点构成的集合为 ,记所有非核心点构成的集合为 。
-
边界点(border-point)
若 ,且 ,满足
即 的 邻域中存在核心点,则称 为 的边界点,记 中所有的边界点构成的集合为 。
此外,边界点也可以这么定义:若 ,且 落在某个核心点的 邻域内,则称 为 的一个边界点,一个边界点可能同时落入一个或多个核心点的 邻域。
-
噪声点(noise-point)
若 满足
则称 为噪声点。
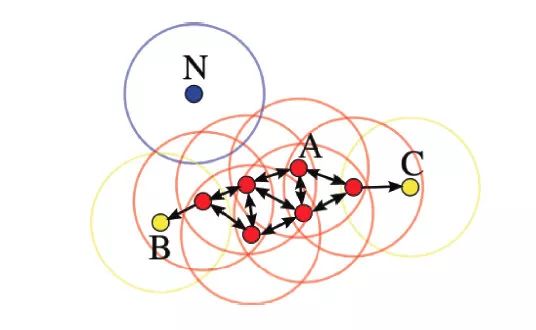
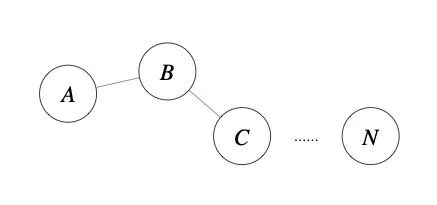
如下图所示,设 ,则A为核心点,B、C是边界点,而N是噪声点。
该算法的流程如下:
标记所有对象为unvisited 当有标记对象时
创建一个新的簇 ,并把 放入 中 设 是 的 邻域内的集合,对 中的每个点 保存 标记 为visited 如果 的 邻域至少有 个对象,则把这些点添加到 如果 还不是任何簇的成员,则把 添加到 如果点 是unvisited 随机选取一个unvisited对象 标记 为visited 如果 的 邻域内至少有 个对象,则 否则标记 为噪声
构建
邻域的过程可以使用kd-tree进行优化,循环过程可以使用Numba、Cython、C进行优化,DBSCAN的源代码,使用该节一开始提到的数据集,聚类效果如下
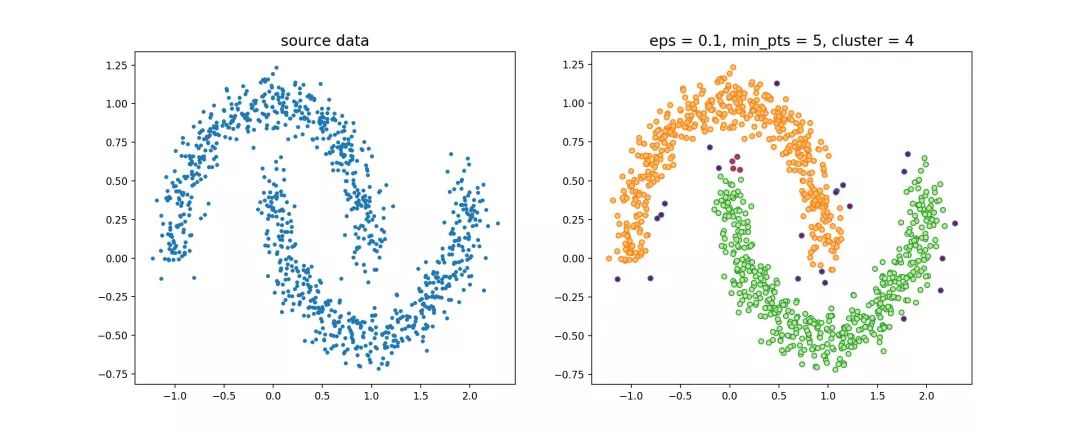
聚类的过程示意图
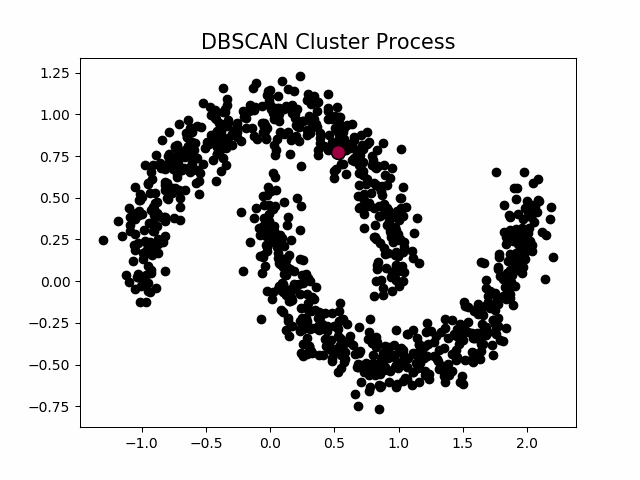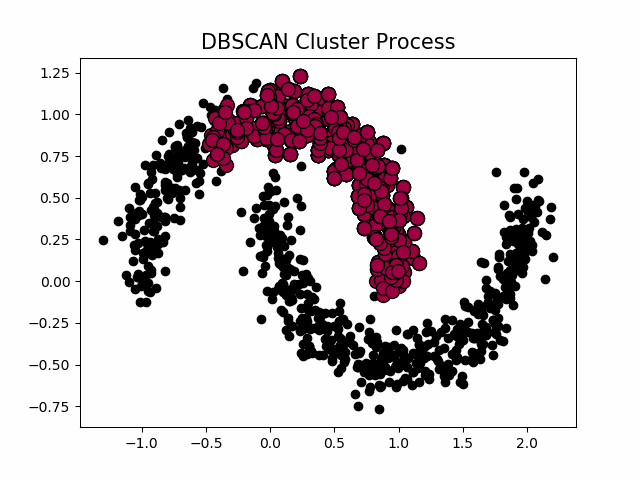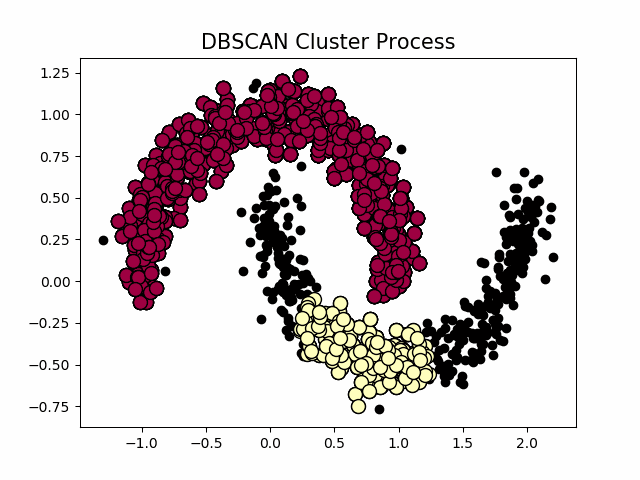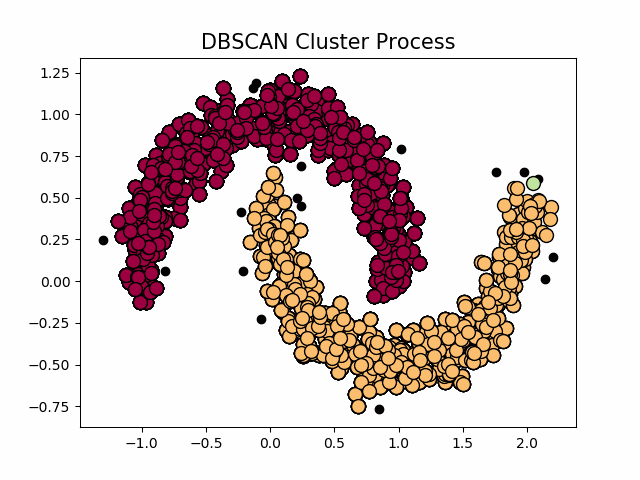
当设置不同的 时,会产生不同的结果,如下图所示
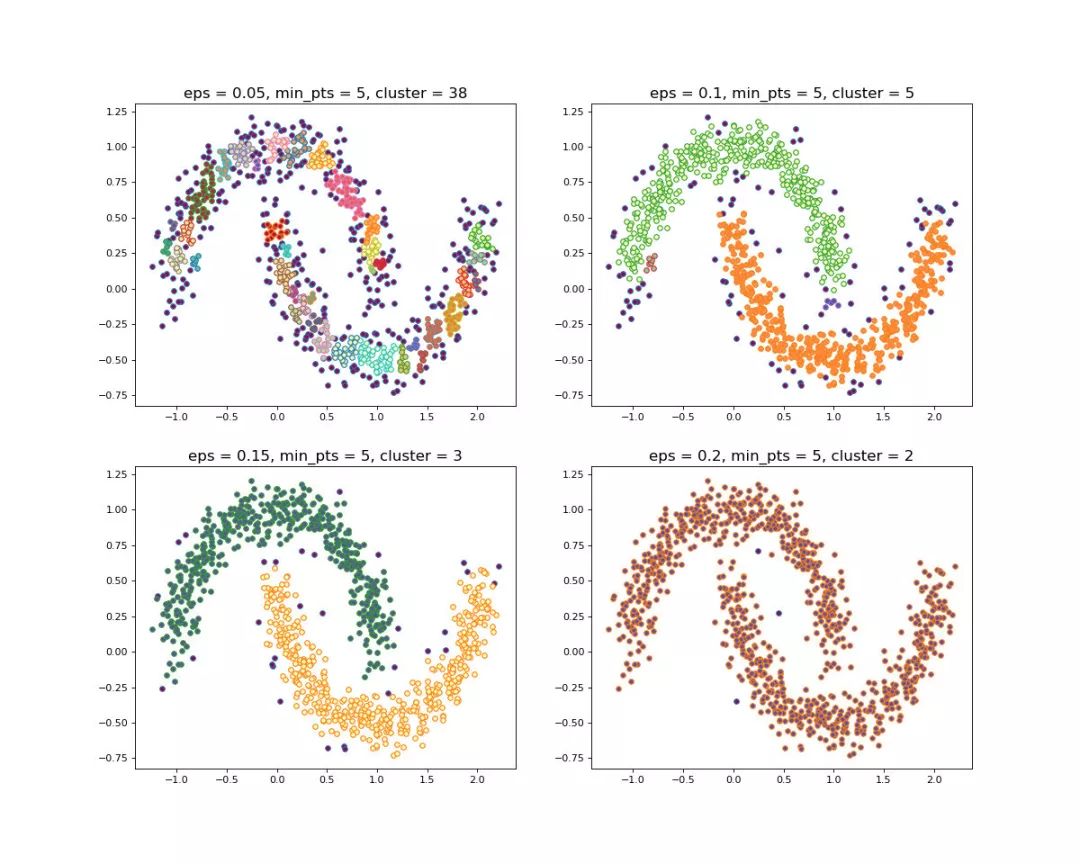
当设置不同的 时,会产生不同的结果,如下图所示
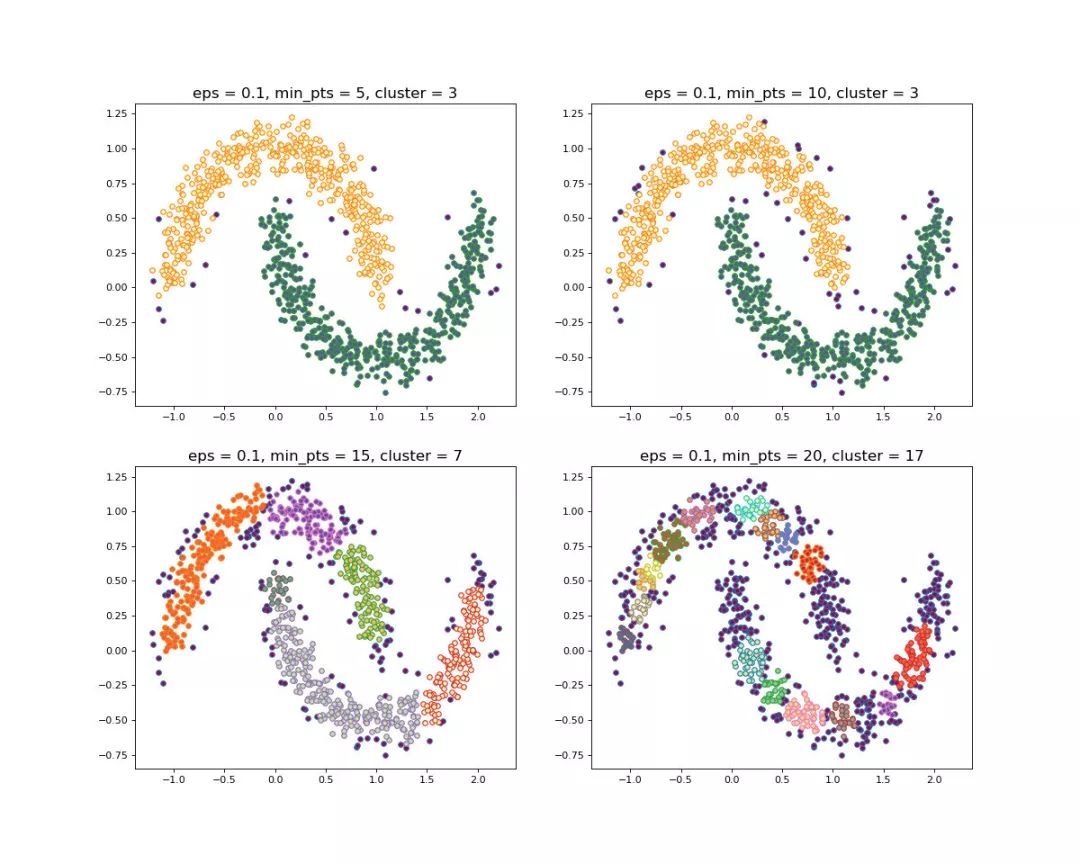
一般来说,DBSCAN算法有以下几个特点:
-
需要提前确定 和 值 -
不需要提前设置聚类的个数 -
对初值选取敏感,对噪声不敏感 -
对密度不均的数据聚合效果不好
2.2.2 OPTICS算法
在DBSCAN算法中,使用了统一的
值,当数据密度不均匀的时候,如果设置了较小的
值,则较稀疏的cluster中的节点密度会小于
,会被认为是边界点而不被用于进一步的扩展;如果设置了较大的
值,则密度较大且离的比较近的cluster容易被划分为同一个cluster,如下图所示。
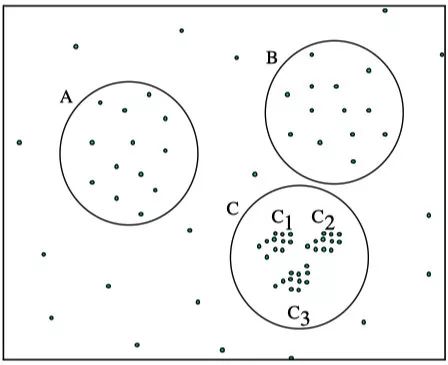
-
如果设置的 较大,将会获得A,B,C这3个 cluster -
如果设置的 较小,将会只获得C1、C2、C3这3个 cluster
对于密度不均的数据选取一个合适的 是很困难的,对于高维数据,由于维度灾难(Curse of dimensionality), 的选取将变得更加困难。
怎样解决DBSCAN遗留下的问题呢?
The basic idea to overcome these problems is to run an algorithm which produces a special order of the database with respect to its density-based clustering structure containing the information about every clustering level of the data set (up to a "generating distance" ), and is very easy to analyze.
即能够提出一种算法,使得基于密度的聚类结构能够呈现出一种特殊的顺序,该顺序所对应的聚类结构包含了每个层级的聚类的信息,并且便于分析。
OPTICS(Ordering Points To Identify the Clustering Structure, OPTICS)实际上是DBSCAN算法的一种有效扩展,主要解决对输入参数敏感的问题。即选取有限个邻域参数
进行聚类,这样就能得到不同邻域参数下的聚类结果。
在介绍OPTICS算法之前,再扩展几个概念。
-
核心距离(core-distance)
样本 ,对于给定的 和 ,使得 成为核心点的最小邻域半径称为 的核心距离,其数学表达如下
其中,
表示在集合
中与节点
第
近邻的节点,如
表示
中与
最近的节点,如果
为核心点,则必然会有
。
-
可达距离(reachability-distance)
设 ,对于给定的参数 和 , 关于 的可达距离定义为
特别地,当 为核心点时,可以按照下式来理解 的含义
可达距离的意义在于衡量 所在的密度,密度越大,他从相邻节点直接密度可达的距离越小,如果聚类时想要朝着数据尽量稠密的空间进行扩张,那么可达距离最小是最佳的选择。
举个🌰,下图中假设 ,半径是 。那么 点的核心距离是 ,点2的可达距离是 ,点3的可达距离也是 ,点4的可达距离则是 的距离。
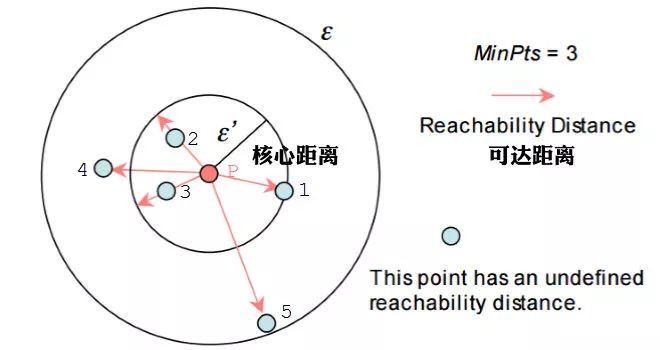
OPTICS源代码,算法流程如下:
标记所有对象为unvisited,初始化order_list为空 当有标记对象时
初始化seed_list种子列表 调用insert_list(),将邻域对象中未被访问的节点按照可达距离插入队列seeld_list中 当seed_list列表不为空 调用insert_list(),将邻域对象中未被访问的节点按照可达距离插入队列seeld_list中 按照可达距离升序取出seed_list中第一个元素 标记 为visited,插入结果序列order_list中 如果 的 邻域内至少有 个对象,则 随机选取一个unvisited对象 标记 为visited,插入结果序列order_list中 如果 的 邻域内至少有 个对象,则
算法中有一个很重要的insert_list()函数,这个函数如下:
对 中所有的邻域点 如果 未被访问过
如果 $rd(k,i) 更新 的值,并按照可达距离重新插入seed_list中 将节点 按照可达距离插入seed_list中 计算 如果 否则
OPTICS算法输出序列的过程:
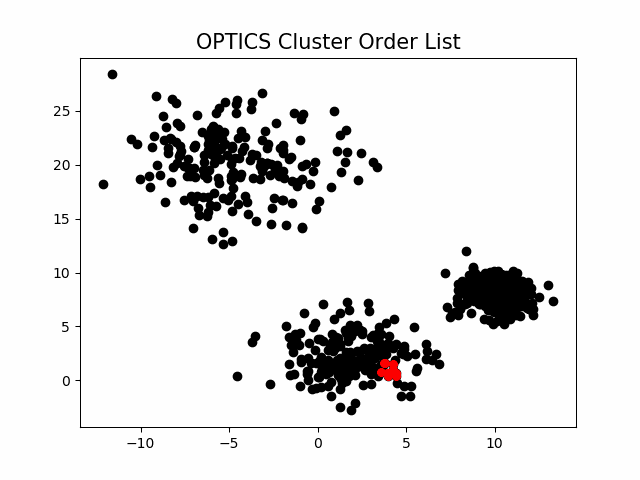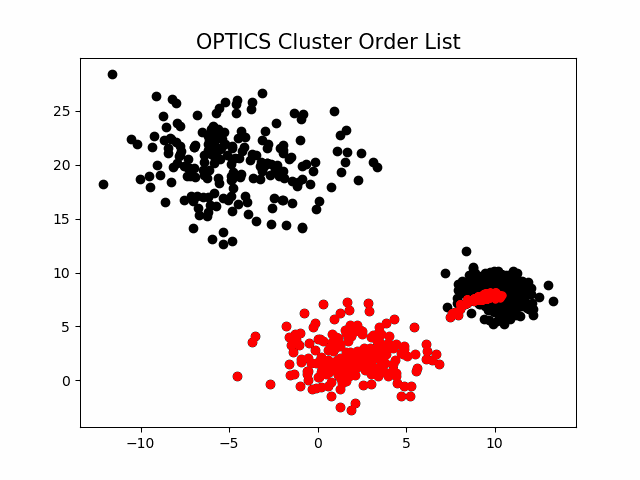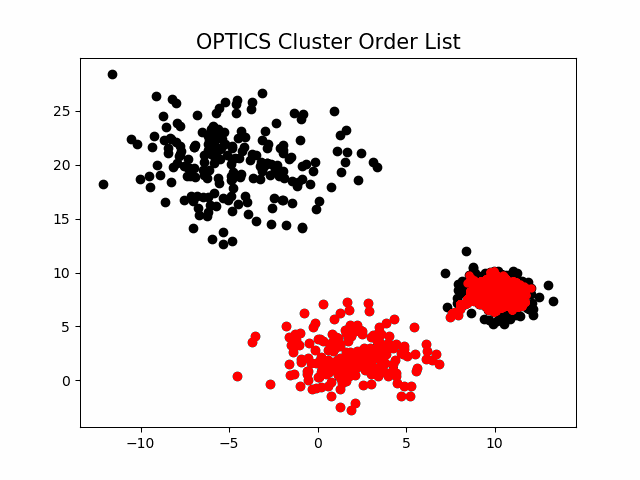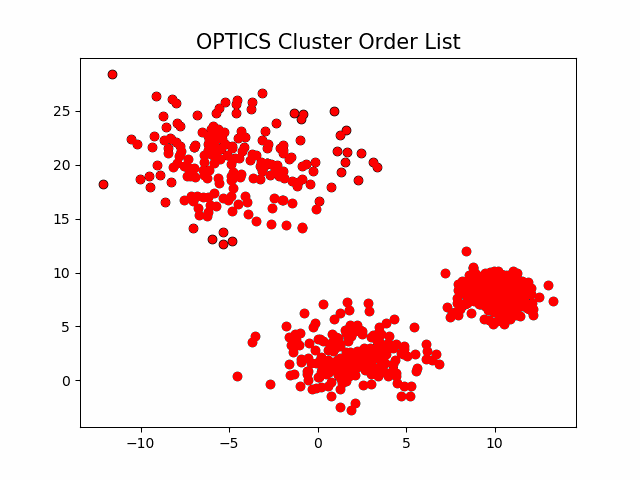
该算法最终获取知识是一个输出序列,该序列按照密度不同将相近密度的点聚合在一起,而不是输出该点所属的具体类别,如果要获取该点所属的类型,需要再设置一个参数 提取出具体的类别。这里我们举一个例子就知道是怎么回事了。
随机生成三组密度不均的数据,我们使用DBSCAN和OPTICS来看一下效果。
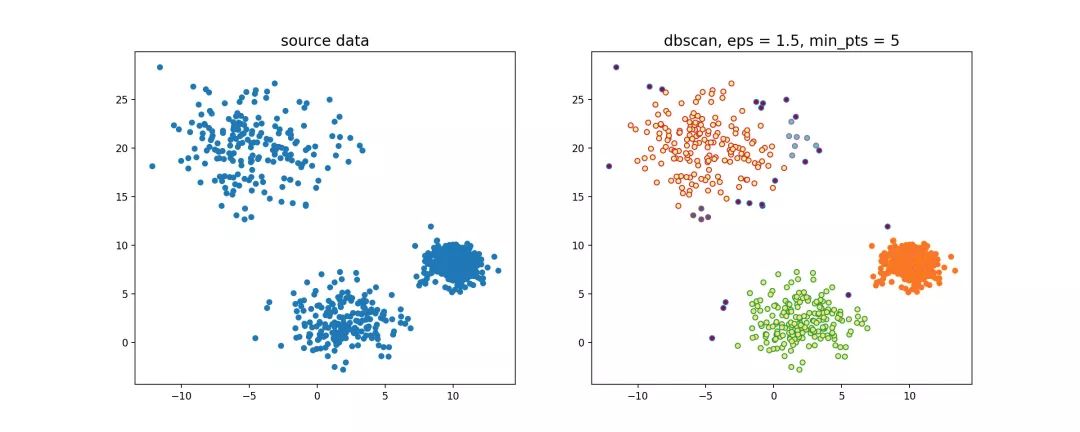
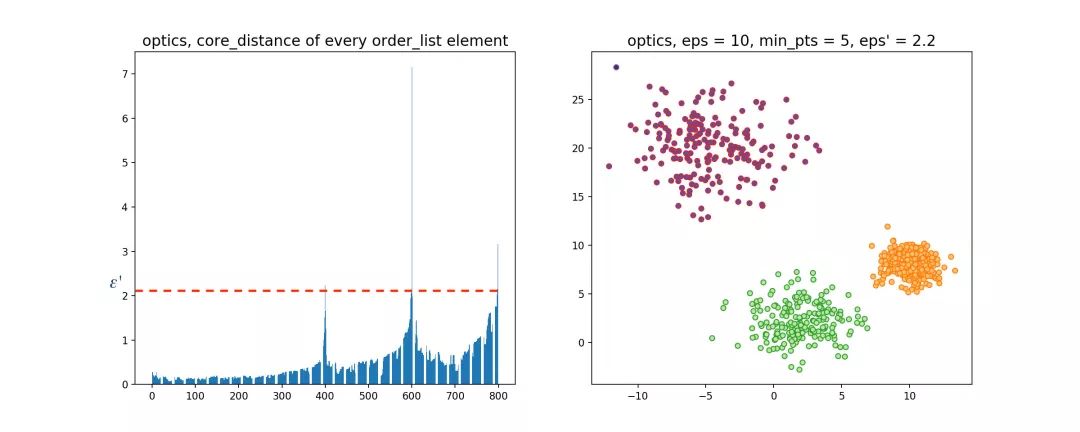
可见,OPTICS第一步生成的输出序列较好的保留了各个不同密度的簇的特征,根据输出序列的可达距离图,再设定一个合理的
,便可以获得较好的聚类效果。
2.3 层次化聚类方法
前面介绍的几种算法确实可以在较小的复杂度内获取较好的结果,但是这几种算法却存在一个链式效应的现象,比如:A与B相似,B与C相似,那么在聚类的时候便会将A、B、C聚合到一起,但是如果A与C不相似,就会造成聚类误差,严重的时候这个误差可以一直传递下去。为了降低链式效应,这时候层次聚类就该发挥作用了。
层次聚类算法 (hierarchical clustering) 将数据集划分为一层一层的 clusters,后面一层生成的 clusters 基于前面一层的结果。层次聚类算法一般分为两类:
-
Agglomerative 层次聚类:又称自底向上(bottom-up)的层次聚类,每一个对象最开始都是一个 cluster,每次按一定的准则将最相近的两个cluster合并生成一个新的cluster,如此往复,直至最终所有的对象都属于一个cluster。这里主要关注此类算法。 -
Divisive 层次聚类:又称自顶向下(top-down)的层次聚类,最开始所有的对象均属于一个 cluster,每次按一定的准则将某个cluster划分为多个cluster,如此往复,直至每个对象均是一个cluster。
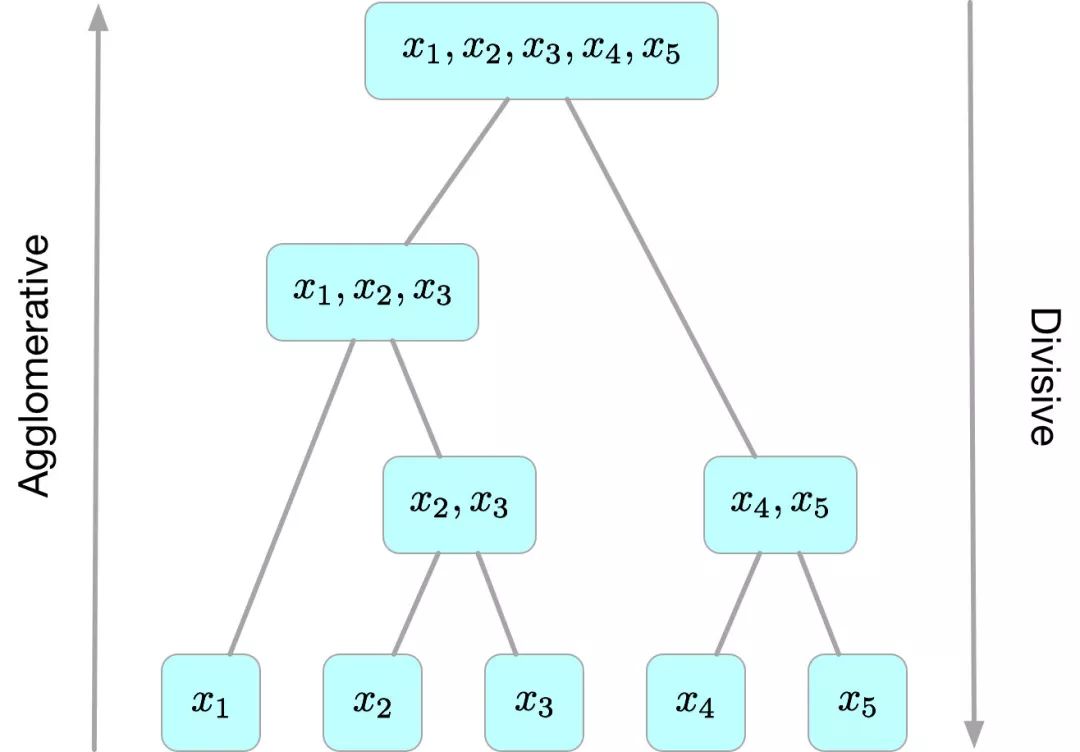
另外,需指出的是,层次聚类算法是一种贪心算法(greedy algorithm),因其每一次合并或划分都是基于某种局部最优的选择。
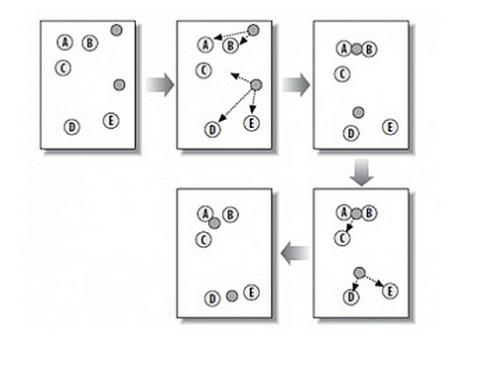
2.3.1 Agglomerative算法
给定数据集
,Agglomerative层次聚类最简单的实现方法分为以下几步:
初始时每个样本为一个 cluster,计算距离矩阵 ,其中元素 为样本点 和 之间的距离;遍历距离矩阵 ,找出其中的最小距离(对角线上的除外),并由此得到拥有最小距离的两个 cluster的编号,将这两个cluster合并为一个新的cluster并依据cluster距离度量方法更新距离矩阵 (删除这两个cluster对应的行和列,并把由新cluster所算出来的距离向量插入 中),存储本次合并的相关信息;重复 2 的过程,直至最终只剩下一个 cluster。
Agglomerative算法源代码,可以看到,该 算法的时间复杂度为
(由于每次合并两个 cluster 时都要遍历大小为
的距离矩阵来搜索最小距离,而这样的操作需要进行
次),空间复杂度为
(由于要存储距离矩阵)。

上图中分别使用了层次聚类中4个不同的cluster度量方法,可以看到,使用single-link确实会造成一定的链式效应,而使用complete-link则完全不会产生这种现象,使用average-link和ward-link则介于两者之间。
2.4 聚类方法比较
算法类型 |
适合的数据类型 |
抗噪点性能 |
聚类形状 |
算法效率 |
|---|---|---|---|---|
| kmeans | 混合型 | 较差 | 球形 | 很高 |
| k-means++ | 混合型 | 一般 | 球形 | 较高 |
| bi-kmeans | 混合型 | 一般 | 球形 | 较高 |
| DBSCAN | 数值型 | 较好 | 任意形状 | 一般 |
| OPTICS | 数值型 | 较好 | 任意形状 | 一般 |
| Agglomerative | 混合型 | 较好 | 任意形状 | 较差 |
三、小区融合项目应用
3.1 小区融合的目的
贝壳找房的楼盘字典目前已成为全国最大的真实房源数据库,该数据库不仅存储了房源的信息,也存储了大量的小区数据,小区融合的目的是通过设置融合策略,将楼盘字典的多份小区数据进行整合,最终形成一个不包含重复小区的数据库。
3.2 聚类方法选择与效果
小区融合项目中,比较两个小区的相似度一般可以通过以下三种途径:
-
比较两个小区的小区名 -
比较两个小区的经纬度 -
比较两个小区的地址
在实际融合中,结合三种途径,设定合理的融合策略,将楼盘字典中的非主小区数据表挂靠到楼盘字典的主小区表中,不能够挂靠到主小区表的数据,使用聚类算法对这些小区进行融合,获取非主小区表中的独有小区。为什么在这里使用聚类呢?因为可以减少不必要的比较次数,在spark程序中,是以城市中的一个城区作为最小的处理单元,该单元中的小区都需要一一比较的话耗时太长,并且容易产生**"链式效应"**。那么聚类算法应该选择什么呢?
根据前面各种聚类算法的比较,我们选择的是DBSCAN和层次聚类算法。具体的融合策略如下图所示。
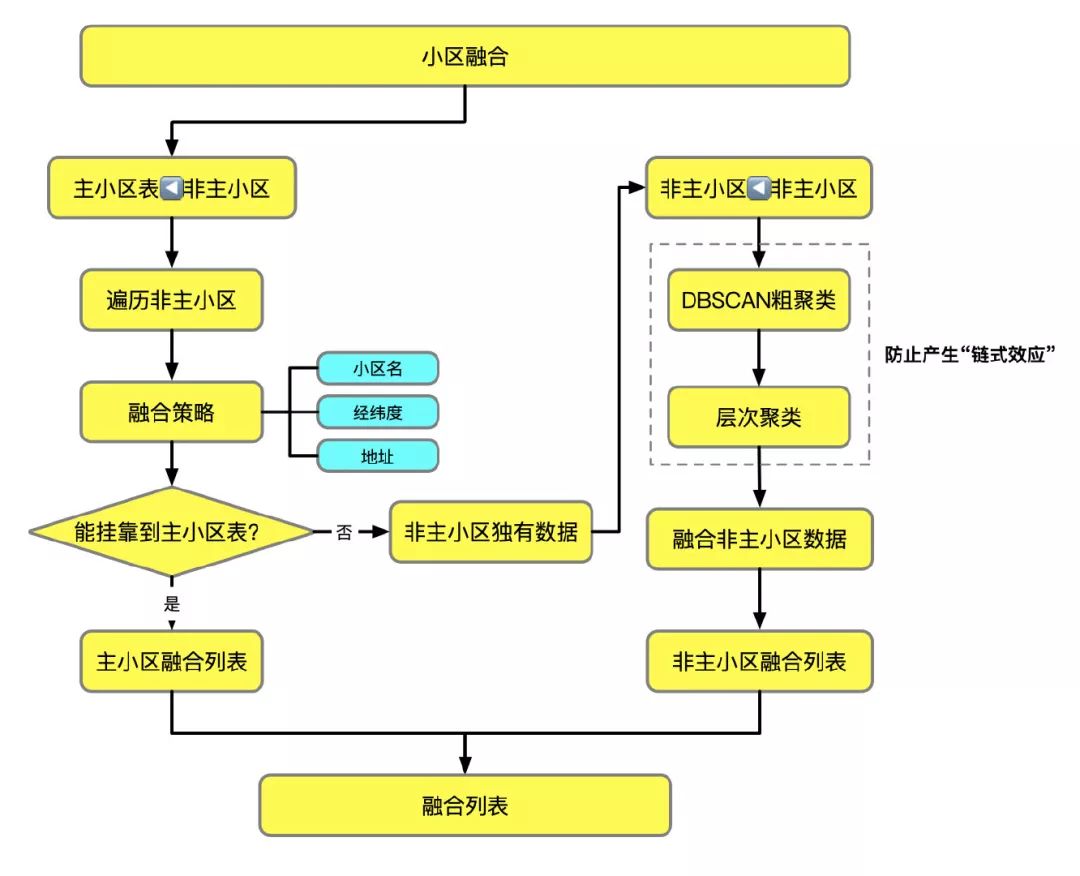
以北京市朝阳区的小区为例,融合之前所有小区的数据量9400,经过融合之后非主小区的独有数据量1345,设置DBSCAN融合阈值eps=500,min_pts=5,得到的融合结果如下图所示
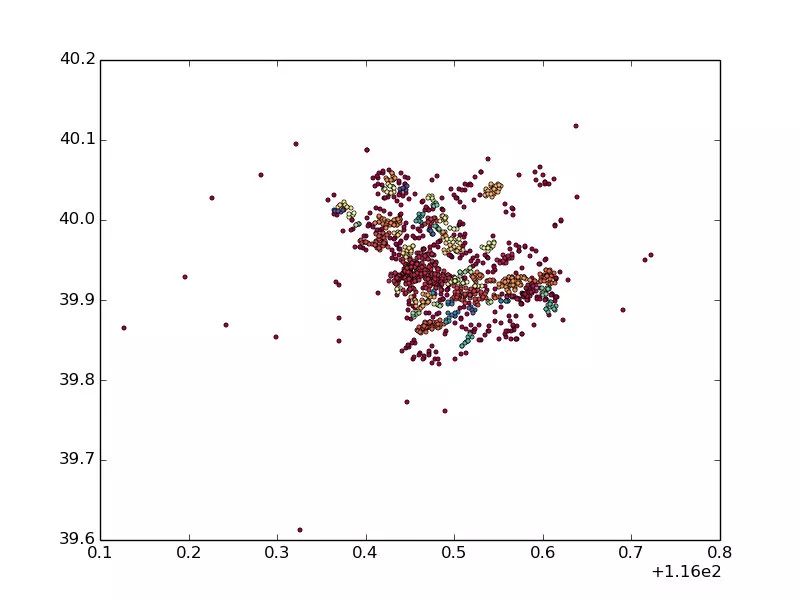
四、参考文献
[1] 李航.统计学习方法
[2] Peter Harrington.Machine Learning in Action/李锐.机器学习实战
[3] https://www.zhihu.com/question/34554321
[4] T. Soni Madhulatha.AN OVERVIEW ON CLUSTERING METHODS
[5] https://zhuanlan.zhihu.com/p/32375430
[6] http://heathcliff.me/聚类分析(一):层次聚类算法
[7] https://www.cnblogs.com/tiaozistudy/p/dbscan_algorithm.html
[8] https://blog.csdn.net/itplus/article/details/10089323
[9] Mihael Ankerst.OPTICS: ordering points to identify the clustering structure
作者介绍
胡著,2019年6月毕业于华中科技大学,现任贝壳找房知识图谱工程师,负责贝壳找房房产知识图谱的研发及落地应用。
推荐阅读
百度PaddleHub NLP模型全面升级,推理性能提升50%以上
斯坦福大学NLP组Python深度学习自然语言处理工具Stanza试用
数学之美中盛赞的 Michael Collins 教授,他的NLP课程要不要收藏?
From Word Embeddings To Document Distances 阅读笔记
模型压缩实践系列之——bert-of-theseus,一个非常亲民的bert压缩方法
可解释性论文阅读笔记1-Tree Regularization
关于AINLP
AINLP 是一个有趣有AI的自然语言处理社区,专注于 AI、NLP、机器学习、深度学习、推荐算法等相关技术的分享,主题包括文本摘要、智能问答、聊天机器人、机器翻译、自动生成、知识图谱、预训练模型、推荐系统、计算广告、招聘信息、求职经验分享等,欢迎关注!加技术交流群请添加AINLPer(id:ainlper),备注工作/研究方向+加群目的。