从一维到十一维（上）

2018 年 2 月 20 日 科研圈

撰文 Margaret Wertheim

翻译卓思琪

审校阿金谭坤金庄维

我正准备伏案疾书，抬手打开桌上的灯，拉开桌下的抽屉，拿出笔。在我面前有妹妹送我的幸运物——一个古怪的小雕像，背后有酣睡的猫主子。右边放着文章的参考资料，左边则是成堆的账单和要回复的信件。上、下，前、后，左、右：我在我的私人三维宇宙内翱翔。大部分西方建筑物由三个相连的直角构成垂线型结构，我的办公室也不例外，这个世界的以三维轴线的方式，无形地包围着我。

我们身边的建筑、学校的教科书以及各类字典都告诉我们：空间是三维的。《牛津英语词典》将“空间”定义为：“一个连续的区域或广阔的场所，空旷不被物质占据……其维度包含高度、深度和宽度，所有物体都在此间存在和运动。”

18世纪的哲学家康德（Immanuel Kant）认为三维欧氏空间（Euclidean space）具有先验（a priori）必然性，就好像我们生活在计算机成像和电子游戏中，依赖笛卡尔坐标系来描述空间。这在今天看来，似乎是不证自明的。

我们所处的空间可以有一定的的数学结构（mathematical structure）——这个理论是西方文化的颠覆性创新之举，意在推翻长久以来对现实世界的本性的认识。虽然人们常把现代科学的诞生描述为向“机械论自然观”的转变，但更重要、当然也更持久的是它为我们带来了“空间是种几何结构”的观念。

在上个世纪，描述空间的几何结构是理论物理学的重大课题，阿尔伯特·爱因斯坦（Albert Einstein）和他的追随者试图将自然中的所有基本作用力视为空间本身的形状的副产品。一般情况下，我们接受的教育告诉我们：空间有三个维度；但广义相对论则描绘了一个四维宇宙图景，而弦论表示有 10 个维度存在——它的扩展理论 M 理论甚至认为有 11 个维度。弦论中有几种模型存在于 26 维，最近还出现了让数学家兴奋不已的 24 维版本。但是，这些“维度”是什么？10 维空间又意味着什么？

为了理解现代数学如何考虑空间，我们首先需要将空间视作一个可以被物体占据的场所。至少，“空间”必须是可以延伸的。虽然看上去是显而易见的概念，但这却是对亚里士多德（Aristotle）的“诅咒”。从古希腊晚期到中世纪，亚里士多德关于物理世界的种种理念一直主导着西方世界的思想。

其实严格来讲，亚里士多德的物理学并不包括空间理论，他仅是提出了空间（place）的概念。想象桌上有一只杯子：亚里士多德认为，杯子本身是一个实体，被空气所包围。在他的世界图景里，不存在“空无一物的空间”，有的只是不同实体之间的间隙：比如，那只杯子和围绕它的空气，或者和桌子之间的边界。他认为，“空间”（如果你想称呼它为空间的话）只是杯子和它周围物质相接处极其狭小的一丝缝儿。如果空间不延展，那么里面什么也装不下。

早在亚里士多德前几个世纪，留基伯（Leucippus）和德谟克利特（Democritus）就已提出一个关于自然世界的理论：他们认为空间是自然世界内部固有的，并建立原子论（atomism）——物质世界由虚空（void）中运动的微小粒子（原子）组成。而亚里士多德不接受原子论，坚称虚空的概念逻辑上就说不通。他从定义上讨论说，“虚无”是不可能存在的。从驳斥亚里士多德对虚空的否定，到接受可扩展的空间这个概念又经历了几个世纪。直到17世纪前叶，伽利略（Galileo）和笛卡尔（Descartes）将空间扩展学说作为现代物理学的基石，“假定物理空间完全等同于几何空间”（——Edwin Burtt），这种革命性的概念才盛行起来。

早在物理学家接受欧氏空间之前，画家才是探寻空间几何概念的先锋人物，也多亏了他们，人类的思想框架才会有这样巨大的飞跃。在中世纪晚期，从柏拉图（Plato）和毕达哥拉斯（Pythagoras）学说——这两位也是亚里士多德学说的主要竞争对手——衍生出一个新的思潮，“上帝根据欧氏几何创造世界”的观点开始在欧洲广为流传。因此，如果画家想要真实地描绘出现实世界，他们就得模仿造物主的表现技巧。14 世纪到 16 世纪间，乔托（Giotto）、保罗·尤切洛（Paolo Uccello）和皮耶罗·德拉·弗朗西斯卡（Piero della Francesca）等艺术家开创出透视法—— 一种最初称为“几何图形”的风格。通过对几何原理的探索，画家们逐渐学会在三维空间内描图绘物。也就是这样，画家们刷新了欧洲人的思维模式，让大家用欧几里德的方式来看空间。

乔托《哀悼基督》

站在透视法前沿的先锋仿佛以上帝视角透视着这个三维世界，发自肺腑地抛弃了亚里士多德的“空间学说”。其中最神奇的一点是，当科学家和哲学家谨慎地挑战亚里士多德对空间的认知时，艺术家则通过感性认识，在知识领域中大胆地闯出一条大道来。他们的透视法类似于现在十分流行的“虚拟现实”（VR）技术，让观看者身临其境地探索其他世界。

“现实世界”的结构由神学和哲学问题演变成了几何命题。

用透视法表现虚拟的欧氏空间深深印刻入欧洲人的意识中，伽利略和笛卡尔则将其运用到真实世界中。值得一提的是，伽利略本人学过透视法，他开创性地描绘月亮主要特征时就展现出本人表现纵深的能力：他描绘的月亮上有高山有深谷，暗示月亮也像地球一样，由坚硬的物质组成。

伽利略能利用空间透视法，按照数学规律描述物体的运动。空间本身是抽象的，它没有特点，稳定存在又不可感知触摸，唯一可知的属性只有欧式几何属性。到了17世纪末，艾萨克·牛顿（Isaac Newton）将伽利略的空间观念扩大到宇宙尺度，宇宙被定义为一个无限的三维空间，它广阔无垠、没有质量，可向四面八方无限延伸。就此，关于“现实世界”的结构，已经从哲学和神学问题转化为几何命题。

当画家已经使用数学工具发展绘画的新方法时，“科学革命”也迎来了曙光，笛卡尔发明出一种新方法，用数学关系来描述图形。在这个过程中，他将维度概念形式化，并将它们根植于我们脑海中。这不仅是观察世界的新方法，更是研究科学的新工具。

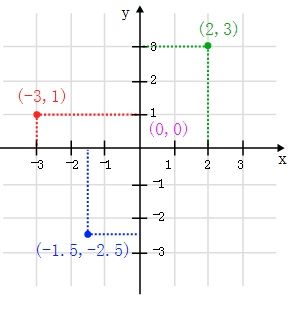
今天，我们几乎每个人都认识笛卡尔这一天才成果——笛卡尔平面（Cartesian plane）。其上的坐标系（coordinate system）是由两条互相垂直的 x 轴和 y 轴形成的直角坐标系统。

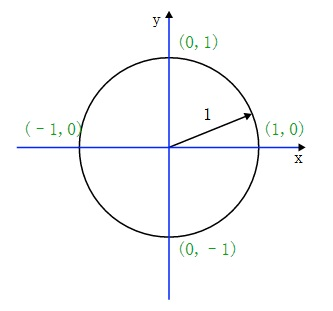
根据定义，笛卡尔平面是一个二维空间，因为我们需要两个坐标值来描述其中的任意一点。笛卡尔发现，他能够在这个框架内将几何图形和代数公式联系起来。例如，半径为 1 的圆就可以用 x² + y² = 1 来描述。

在这个平面内，我们绘出的大部分图形都能用公式来表示。而这种“解析几何”，或者“笛卡尔几何”，很快就成为微积分的基础。微积分是由牛顿和莱布尼茨（G W Leibniz）发展而来，并且很快成为物理学家分析运动的工具。了解微积分的方式之一就是研究曲线。微积分能帮助我们确定曲线在哪里最陡，某一段曲线的极值点等等。在研究运动时，微积分能预测物体抛出后达到最高点的位置，或者斜面上滚动的小球达到某一具体速度的时间等。微积分应用广泛，自诞生以来几乎成了所有分支学科的重要工具。

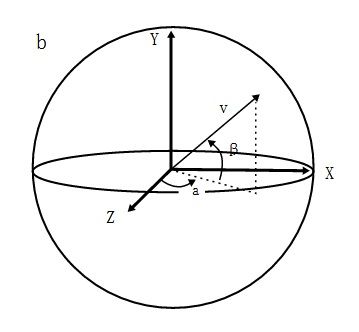
由二维坐标出发，我们很容易想到添加第三个坐标轴。因此，我们可以用 x、y 和 z 轴来描述一个球面，比如半径为 1 的球面就可以用公式 x²+ y² + z² = 1 来表示。

这三个轴能够用来描述三维空间的形式。同样地，每个点需要由三个坐标共同确定。

我们不要停下脚步，尝试一下添加第四个维度会怎样。比如说再加个 p 轴。现在，我写下一个公式 x² + y² + z² + p² = 1，这代表一个四维球。虽然我画不出来这个物体，但是从数学上讲，再增加一个维度是合理的。“合理”意味着没有任何逻辑上的错误，因此理论上讲我没有理由不能增加这个额外的维度。

维度成为了纯粹的概念符号，它不再需要和物质世界联系在一起。

我们还可以继续添加更多的维度。那么我就可以在五维空间定义一个五维球（五维坐标 x, y, z, p, q）：x²+ y² + z²+ p² + q²= 1。再加一个维度变成六维：x² + y² + z² + p² + q²+ r² = 1，以此类推。

尽管我可能无法画出更高维的球面，但是我能够把它们用符号表示出来。这也是理解数学史的一种方式——逐渐超越看似合理的事物。就像刘易斯·卡罗尔（Lewis Carroll）在《爱丽丝镜中奇遇记》（Through the Looking Glass, and What Alice Found There）借白皇后之口宣称：“我有能力在早餐之前相信六件不可能的事情。”

在数学上，我可以在任何维度下描述球面。而我需要做的，就是不断增加坐标轴——数学家称之为“自由度”（degrees of freedom）。传统上它们被命名为 x1, x2, x3, x4,x5, x6 等。如同笛卡尔平面上的点可以用两个坐标点（x, y）来描述，17 维空间中的点就可以用 17 个坐标点（x1, x2, x3, x4,x5, x6 ...x15, x16, x17）来表示。上面那些多维空间中的球面通常被称为流形（manifolds）。

从数学的角度来看，一个“维度”只不过是一个坐标轴（或者是一个自由度）。它最终成为一个纯粹的符号，没有必要和物质世界联系在一起。19世纪60年代，逻辑学家奥古斯都·德·摩根（Augustus De Morgan）总结出“数学领域愈渐抽象”的观点，指出数学是纯粹的“符号科学”，数学只需要它自身，不需要再指涉任何其他事物。从某种意义上说，数学就是让逻辑在想象力领域内为所欲为。

和在思想领域毫无拘束的数学家不同，物理学必须要和自然界联系在一起，至少原则上，它要和物质联系在一起。然而，这一切也都有摆脱限制的可能性：如果数学上允许超过三维，并且我们承认数学可用来描述世界，那么我们怎么知道物理空间仅限于三维呢？尽管伽利略、牛顿和康德都将长度、宽度和高度这三个维度视作不言自明的，但这个世界上就没有更多的维度了吗？

历史再次重演，艺术媒介在多维宇宙的思想传播上又一次发挥了重要的作用，而这次是通过文学作品。著名数学家艾德温·阿尔伯特（EdwinA Abbott）在社会讽刺小说《平面国》（Flatland）（1884）中描写到：生活在平面国的谦卑正方形受到来自三维空间国的球王的激励，造访壮观的三维立体世界。在空间国，正方形见到了他的三维版本——立方体。接下来，他开始梦想有四维、五维、六维世界。为什么不是超立方体呢？他想知道，是不是还有超超立方体？

但是悲剧的是，当正方形回到平面国后，他被当做一个疯子，关进精神病院。这个故事告诉我们的道理之一就是承认炫耀社会习俗的危险性。当正方形在为其他空间维度的存在辩护时，他也在努力地寻找着相关例证——他就是个数学怪人。

在十九世纪末二十世纪初，一批作家、艺术家和思想家对多维思想的传播做出了贡献。其中包括数学家、科幻小说家查尔斯·汉顿（Charles Hinto）为四维立方体创造了“tesseract”一词，艺术家萨尔瓦多·达利（SalvadorDalí）和神秘主义思想家邬斯宾斯基（P D Ouspensky），他们探讨了四维的思想及其对人类的影响。

1905 年，一位叫阿尔伯特·爱因斯坦（AlbertEinstein）的“无名”物理学家发表了一篇论文，将现实世界描述为一个四维环境。在他的“狭义相对论”中，时间作为新的维度，添加在经典的三维空间上。在相对论的数学形式中，四个维度被绑定在一起，而“时空”这个词也被载入字典——这两个字的组合可不是随意而为的。爱因斯坦发现，沿着这个思路继续下去，一个强大的数学工具应运而生——它超越了牛顿的物理学，能用于预测带电粒子的行为。只有在四维世界中，才能完全、精确地描述电磁学。

相对文学作品而言，相对论要深刻得多。特别是后来爱因斯坦将“狭义相对论”扩展到“广义相对论”。现在，多维空间已经不再虚空，它饱含深刻的物理意义。

在牛顿的世界图景中，物体在自然力（特别是引力）的作用下，在一定时间、空间内运动。空间、时间、物质和力是不同的现实范畴。在狭义相对论中，爱因斯坦证明时间和空间是统一的，从而将基本物理范畴从四个缩减为三个：时空、物质和力。广义相对论在此基础上又迈出一步——它将引力加入时空的结构中。从四维角度来看，引力只是空间形变的产物。

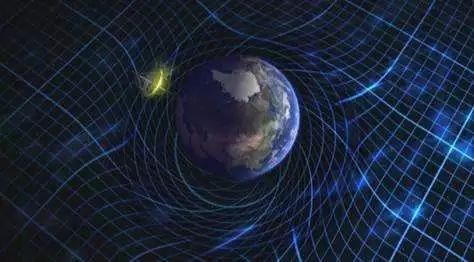
为了理解这一点，我们先考虑二维世界中的情形。我们在一张蹦床上画上笛卡尔网格，然后将一个保龄球放在网格上。这样，球周围的表面会变形，一些点之间的距离变得比之前更远。这是因为我们打乱了空间内距离的固有尺度，使它变得不均衡。广义相对论认为，类似这样的变形就是重物体（例如太阳）对时空的作用，产生了我们熟悉的引力现象。

相比牛顿物理中来历不明的引力，爱因斯坦的理论认为引力来自四维流形的固有几何属性。流形中拉伸最厉害的地方，或者偏离笛卡尔规范最远的地方，引力就越强。我们有时把它称为“橡胶弹性物理学”（rubber-sheet physics）。这里，巨大的宇宙力量只不过是空间弯曲的副产物，它使行星围绕恒星旋转、恒星围绕星系中心旋转。引力就表现为时空的几何。

如果四维时空有助于解释引力，那么五维有什么科学优势呢？为什么不继续研究下去呢？一位年轻的波兰数学家西奥多·卡卢扎（Theodor Kaluza）曾在 1919 年思考：爱因斯坦将引力吸收进时空中，或许在下一个维度中，我们同样可以将电磁力看做是时空几何的副产物？于是，卡卢扎就在爱因斯坦方程中添加了一个维度，然后他欣喜地发现，在五维中，两种力都能在几何模型中完美出现。

从一维到十一维（下）预告：

· 你是一只蚂蚁，爬行在细长的软管上，却从未注意脚下是一个环形维度。

· 我们身处的可能只是众多宇宙中的一个。在五维空间的更广阔舞台上，每个宇宙都是独立的四维泡泡

原文链接

https://aeon.co/essays/how-many-dimensions-are-there-and-what-do-they-do-to-reality

阅读更多

▽ 故事

· 狗年来啦：那些“活跃”在科研界的狗狗们

· 世上最浪漫的事，是和你一起拿诺奖

· 这一年值得一读再读的学术圈好文，就在这里 | 科研圈推荐

· 担心研究成果被抢发？这家近10分的期刊决定接受“第二名”论文投稿

· 压力大了想睡觉？因为这可能修复DNA | Genetics 论文推荐