科学家发现自旋阻挫重费米子体系中的量子临界相
当一个二级相变通过非温度控制的外参量被连续压制到绝对零度附近时,体系会发生量子相变。发生量子相变的临界点,即量子临界点,是绝对零度条件下位于外参量轴上的一个点,通常可以通过调控压力、磁场等手段来获得。量子相变和有限温度下由热涨落控制的相变不同,其物理本质是基于海森堡不确定原理的量子涨落行为。量子相变在重费米子、非常规超导、量子自旋以及冷原子等不同系统中均得到了广泛深入的研究,是产生奇异集体激发模式和新物性的一个重要途径。尤其重要的是,量子临界点虽然产生于绝对零度附近,但是其相关的量子涨落却可以深刻地影响有限温度下的物理行为。很多非常规物理性质,包括高温超导,都可能和量子临界涨落有密切的关系。
重费米子材料是量子临界行为研究的理想体系。这类材料中,传导电子和局域f/d电子间能带杂化产生近藤效应,进而屏蔽局域磁矩。与此同时,局域磁矩间具有RKKY间接交换相互作用,导致磁矩安定化并趋于磁有序。这两个矛盾的物理过程在重费米子材料中相互竞争,产生量子临界现象,甚至非常规超导。另一方面,对于自旋阻挫效应的研究主要集中在绝缘的量子自旋体系,是凝聚态物理的另一个重要研究方向。在该类体系中,自旋阻挫引起的量子涨落会破坏长程磁有序,并可能导致绝对零度下的自旋液体等新奇物态。在具有金属行为的重费米子体系中引入自旋阻挫,将增强低温下的量子涨落,并和传导电子媒介的长程RKKY交换相互作用形成竞争。这时体系的量子临界行为会如何演变,是一个重要的基础物理问题。
近日,《自然-物理》(Nature Physics)杂志发表了中国科学院物理研究所/北京凝聚态物理国家研究中心极端条件物理重点实验室EX9组研究员孙培杰团队博士生赵恒灿、张佳浩等人和莱斯大学教授Q. Si以及马普所教授F. Steglich的合作研究成果。他们发现当重费米子体系的近藤晶格位于阻挫kagome格子时,通过磁场和压力调控,体系会产生一个在压力磁场相图上很宽的、安定的量子临界相。压力下的电阻率、磁化率和比热等测量表明,自旋阻挫导致的量子涨落是产生该量子临界相的主要原因。和其他各类材料中常见的量子临界点不同,相图空间上广域的量子临界相的发现预示着一个由量子涨落导致的稳定新物态的产生。同时,研究团队还发现该量子临界相具有非费米液体等奇异的物理性质。
该研究关注的重费米子材料CePdAl具有变形的kagome阻挫结构。自旋阻挫在很大程度上降低了该材料的反铁磁有序温度,并在磁有序温度以上形成很强的短程自旋关联,表现为磁化率的宽峰。通过构建该材料在极低温下的磁场、压力和温度的三维相图,研究团队发现该材料在反铁磁有序被磁场或压力压制以后,并没有进入非磁性的重费米子态,而是形成了一个在很宽压力和磁场范围内的量子顺磁态。该物态具有局域磁矩,但是在绝对零度附近也没有形成长程磁有序,具有金属自旋液体的特征。区别于常规的量子临界点,绝对零度下这一由量子涨落导致的区域被称为量子临界相。继续增加压力或磁场,该量子临界相可以被压制,体系发生局域巡游转变,进入重费米子态。这一发现对于探索和理解量子涨落导致的非常规金属行为具有重要的意义。
《自然-物理》还同期发表了德国马普复杂系统物理研究所博士Aline Ramires应邀撰写的题为Frustration can be critical 的评述文章,对该研究工作的物理意义进行了详细的评述。
上述研究得到科技部(2017YFA0303100,2015CB921303,2018YFA0305702)、国家自然科学基金委(11774404,11474332,11574377,11874400)以及中科院(XDB07020200)的支持。参与该工作合作研究的还包括德国奥格斯堡大学教授P. Gegenwart团队,日本富山大学教授Y.Isikawa,物理所研究员杨义峰、陈根富、程金光和副研究员张帅等。
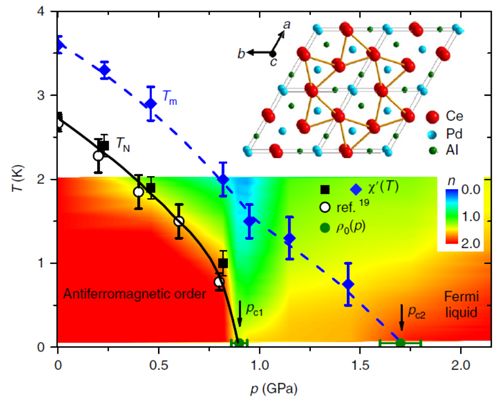
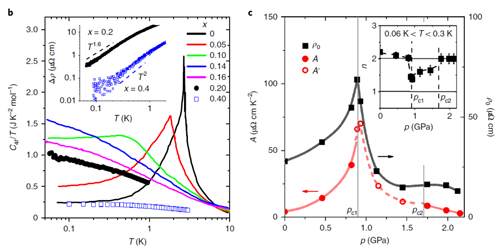
图1:CePdAl中压力诱导量子临界相的产生。(a) 温度-压力相图和电阻率的温度指数。(b) 通过掺杂产生的化学压力表现出和静水压同样的结果,在量子临界相中具有发散的电子比热系数。(c) 电阻率的A系数和残留电阻对应两个临界压力,中间区域代表量子临界相。
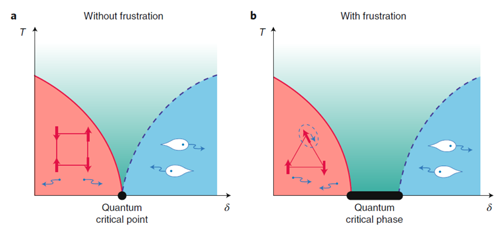
图2:非自旋阻挫体系中的量子临界点和自旋阻挫体系中的量子临界相的对比。
来源:中国科学院物理研究所
温馨提示:近期,微信公众号信息流改版。每个用户可以设置 常读订阅号,这些订阅号将以大卡片的形式展示。因此,如果不想错过“中科院之声”的文章,你一定要进行以下操作:进入“中科院之声”公众号 → 点击右上角的 ··· 菜单 → 选择「设为星标」