CVPR 2020 | GraphTER：通过逐点变换实现无监督图神经网络共变特征学习

2020 年 5 月 9 日 CVer

点击上方“CVer”，选择加"星标"或“置顶”

重磅干货，第一时间送达

本文作者： 齐国君

https://zhuanlan.zhihu.com/p/138368096

本文已由原作者授权，不得擅自二次转载

GraphTER: Unsupervised Learning of Graph Transformation Equivariant Representations via Auto-Encoding Node-wise Transformations

Xiang Gao, Wei Hu, and Guo-Jun Qi

论文：https://arxiv.org/abs/1911.08142

代码：https://github.com/gyshgx868/graph-ter

本论文已被CVPR2020收录，是我们Auto-Encoding Transformations (AET)模型在图计算神经网络上的扩展，并被应用于3D点云数据的分类和分割问题中。

关于更多 AET在不同问题(无监督图像训练、GAN 模型的训练）上的应用，欢迎点击下面的回答。

https://www.zhihu.com/question/372070853/answer/1036736647

一、引言

图（Graph）是不规则数据/非欧几里得数据（例如3D点云、社交网络、引文网络、脑网络等）的一种自然而有效的表征。由于图的强大表现力，图数据的机器学习越来越受到重视，如近年来提出的图卷积神经网络（Graph Convolutional Neural Network, GCNN）。不过，现有的GCNN模型大多以监督或半监督的方式进行训练，这需要大量的标记样本才能学习到有效的特征表示。由于标记成本较高（特别是在大规模的图上），现有方法难以进行广泛应用。因此，我们需要以无监督的方式来学习图特征表示，以便适应更多图的学习任务。

代表性的无监督学习方法包括自动编码器（Auto-Encoders，AEs）和生成对抗网络（Generative Adversarial Networks，GANs）。基于AE和GAN，许多方法通过学习“变换共变表征”（Transformation Equivariant Representations，TERs）来进一步提高无监督特征学习的质量。在TER学习中，通常假定在数据上施加变换会引起数据特征空间的共变，因此能够从变换前的和变换后的数据的特征表示中重构施加在数据上的变换，以此来学习数据的特征表示，如Zhang等人提出的AET [1]。然而，AET着重于对图像进行变换共变表征进行学习，难以直接拓展到非欧几里得空间的图数据。

因此，在本文中我们提出在自动编码器框架下，以无监督的方式编码图中节点的变换方式来实现“图变换共变表征”（Graph Transformation Equivariant Representations，GraphTER）学习，如图1所示。我们的方法的创新性体现在两个方面：1）我们定义图信号变换，并提出了一种基于图的自动编码器网络。该网络对原始图和变换后的图进行编码，以便可以从这两种特征表示中重建出图信号上的变换；2）相比于将全局空间变换应用于整个图像的AET，我们对图上的节点进行逐点变换，使得每个节点可以具有不同的变换。因此，通过借助节点邻居信息来解码这些节点的变换能够揭示节点所在邻域的图结构，进而学习各个节点的特征表示。这些特征表示不仅能够捕获节点周围的局部图结构，而且通过在每个训练迭代中随机采样部分节点进行变换来揭示图的全局信息。该论文的arxiv链接是arxiv.org/abs/1911.0814，代码已经开源在：github.com/gyshgx868/gr

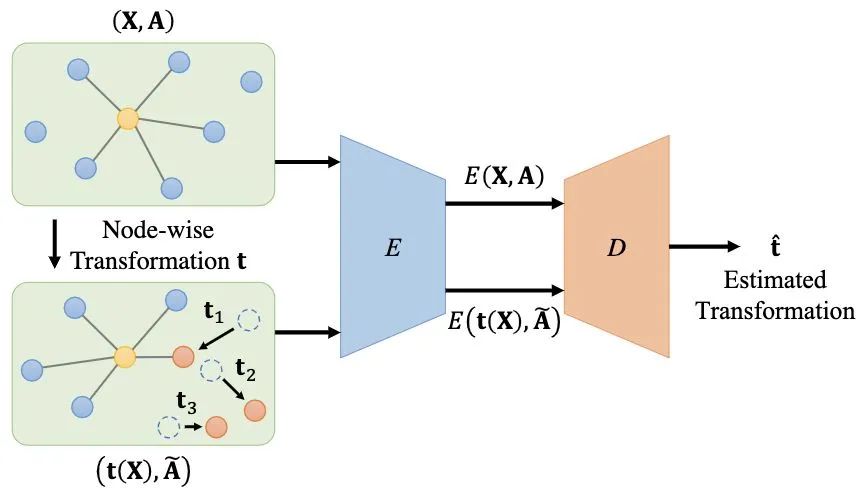
图1：我们提出的无监督图特征学习方法GraphTER。编码器E分别对原始图信号X和邻接矩阵A，以及变换之后的图信号 X ̃ 和邻接矩阵A ̃进行特征学习。解码器D从这两种特征表示预测节点变换，从而使得自动编码器能够学习到图的本质特征。

二、图信号变换

与传统的欧几里得数据（例如图像等）不同，图信号是不规则的，因此难以定义其变换。我们将图信号变换定义为对节点上信号的滤波，如对每个节点独立滤波（平移、旋转等），或考虑邻域信息对节点进行低通/高通滤波。

假设我们从整个变换分布中采样图信号变换。将该变换应用于从数据分布中采样的图信号上，我们便得到了变换后的图信号：

变换t将应用于每个节点，与t相关联的每个节点信号的变换可以彼此不同。例如，对于平移变换，我们可以将不同的平移量应用于不同的节点。如果每个节点的变换是相同（不同）的，我们将该变换称为各向同性（各向异性）的。与变换后的图信号关联的的邻接矩阵为

其中是线性或非线性函数，应用于每对节点以获得其相似性。例如，一种广泛采用的是根据节点特征构建近邻（k-nearest-neighbor，-NN）图。这样我们得到了变换后的图，因为中边的权重也间接地通过t进行变换。

在本文中，我们专注于逐节点图信号变换，即每个节点各向同性或各向异性地具有自己的变换。这种做法有两个优点：

（1）通过对逐节点应用变换，我们可以在图中采样部分节点来研究在各种变换下图的不同部分的特征；

（2）通过解码节点的变换，我们能够学习单个节点的特征表示。此外，这些节点的特征表示不仅能够捕获局部图结构信息，而且在每个训练迭代中随机地采样部分节点施加变换，随着训练迭代的增加还能够学习到全局的图结构信息。

三、方法

给定一组包含个节点的图信号，在每个训练迭代中, 我们遵循样本分布，随机地从图中的所有节点全局或局部地采样节点子集S，即。全局采样是指在全局范围内对整个图的所有节点进行随机采样，而局部采样则仅限于图中的一组局部节点。

图2：在3D点云上展示不同的采样方法（全局或局部）和逐节点平移方法（各向同性或各向异性），红色和蓝色点分别表示经过变换的点和原始点。为了能够清晰地展示，我们将整个机翼作为局部采样的点集。

然后，我们对S中的每个节点施加节点变换（各向同性或各向异性），如图2所示。与此同时，与变换后的图信号关联的邻接矩阵也在变换t下与A共变。如图3所示，我们构造了一个k-NN图，在对采样的节点进行变换之后，邻接矩阵A中表示的连通信息也会随之改变。

图3：进行逐节点变换前后的-NN图示例。我们首先以黄色节点为中心构建k-NN（ k=5 ）图（其他连接略去）。然后，我们在部分蓝色节点上进行平移变换，从而改变了黄色节点周围的图拓扑结构。

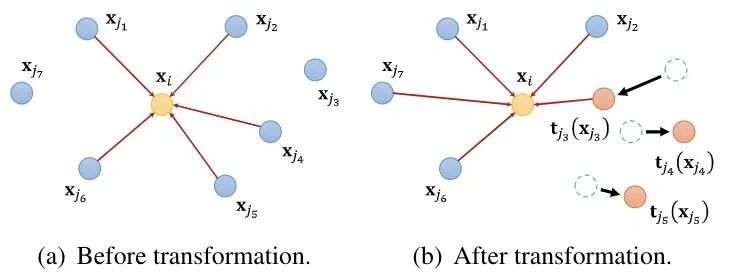
具体来说，给定图信号和与其对应的邻接矩阵，以及经过t变换的图信号和邻接矩阵，如果函数满足下述等式，那么我们称则函数是满足“变换共变性”的：

其中表示在特征空间中的同态变换。

我们设计了自动编码器网络来学习变换共变表征：编码器对图中节点的特征表示进行编码，而解码器从编码器学习到的原始和变换后的图信号的特征表示中估算逐节点变换。

为了估计逐节点变换，我们应用损失函数来最小化逐节点变换和估计的变换之间的差异。这时，整个自动编码器网络便可以通过最小化下面的损失函数进行训练：

在上述公式中，从解码器估计的逐节点变换表示为：

因此，我们通过反向传播该损失来迭代地更新编码器E和解码器D中的参数。

为了估计这些逐节点变换，我们设计了图卷积自动编码器网络，如图4所示。我们选择一种图卷积方法EdgeConv [2]作为自动编码器网络的基本构建模块，该图卷积通过聚合每个节点和其周围邻居的特征来学习节点的特征表示。

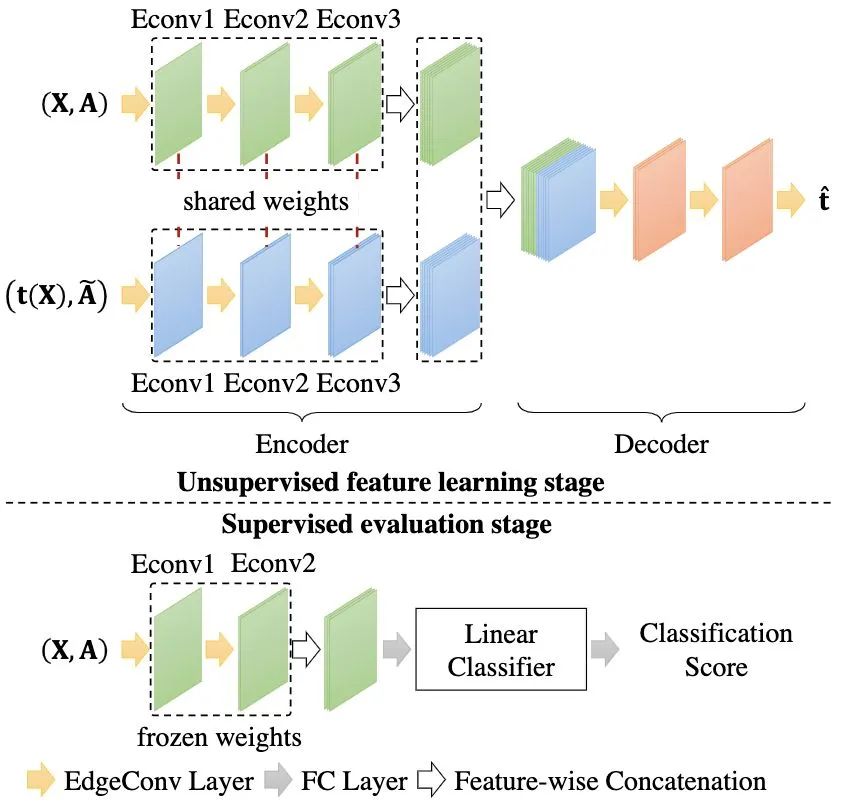
图4：GraphTER自动编码器网络结构。在无监督特征学习阶段，特征编码器和变换解码器将在无标签的样本上进行训练。在评估阶段，我们提取编码器的前几个EdgeConv模块，冻结其权重作为特征提取器，并使用标记的样本训练线性分类器完成特征的分类。

三、实验结果

我们以3D点云分类任务和分割任务为例来验证我们提出的GraphTER模型。

1. 3D点云分类

我们在ModelNet40数据集上来验证GraphTER模型。在该数据集中，我们将3D点云中的点视为图上的节点，3D点坐标视为图信号，并通过点坐标间的欧氏距离在点云上建立k-NN图（）。

表1展示了3D点云的分类结果，在实验中我们选取25%的节点应用各向同性的逐节点剪切（Shear）变换。我们与无监督方法和有监督方法进行比较。GraphTER模型在ModelNet40数据集上达到了92.0％的分类准确率，这优于最新的无监督方法。大多数的无监督模型都结合了GAN和AED的思想，例如FoldingNet，MAP-VAE和L2G-AE。结果表明，GraphTER模型相比于这些方法都有显著的提高，表明了GraphTER模型优于GAN和AED。此外，无监督的GraphTER模型还可以达到与全监督模型结果相当的分类准确率，这极大地缩小了无监督方法与全监督方法之间的差距。

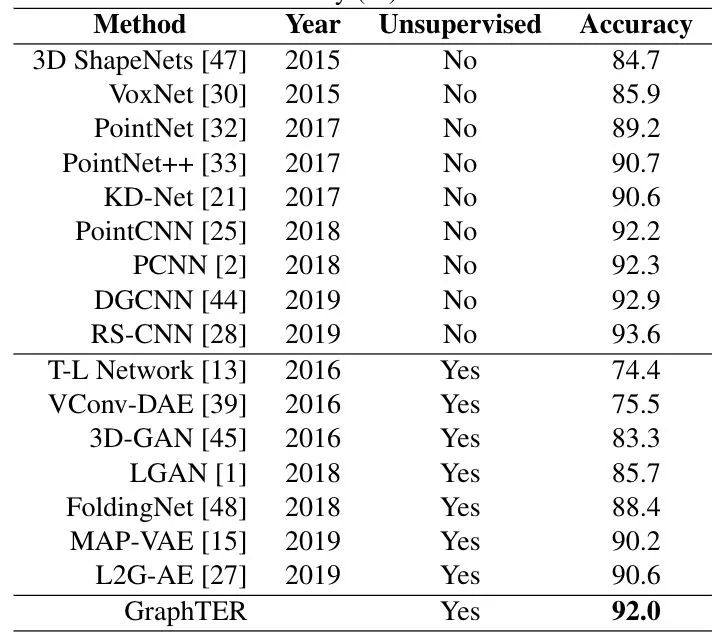
2. 3D点云分割

在该任务中，我们使用ShapeNet part数据集来验证我们的模型。我们同样将GraphTER分别同无监督方法和有监督方法进行比较，如表2中所示。我们的模型达到了81.9％的mIoU，这比最先进的无监督方法MAP-VAE提升了13.9％。此外，无监督的GraphTER模型还可以达到与最新的全监督的方法相当的性能。

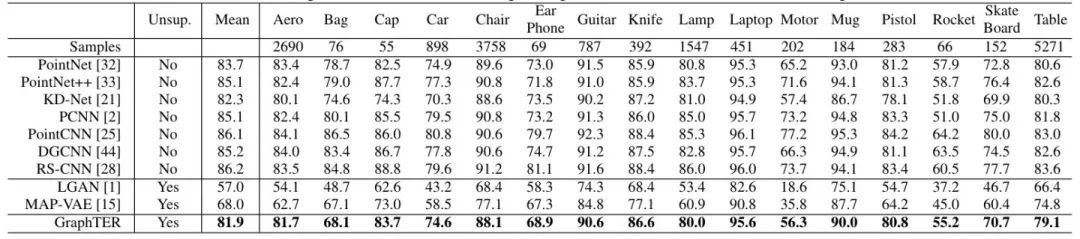
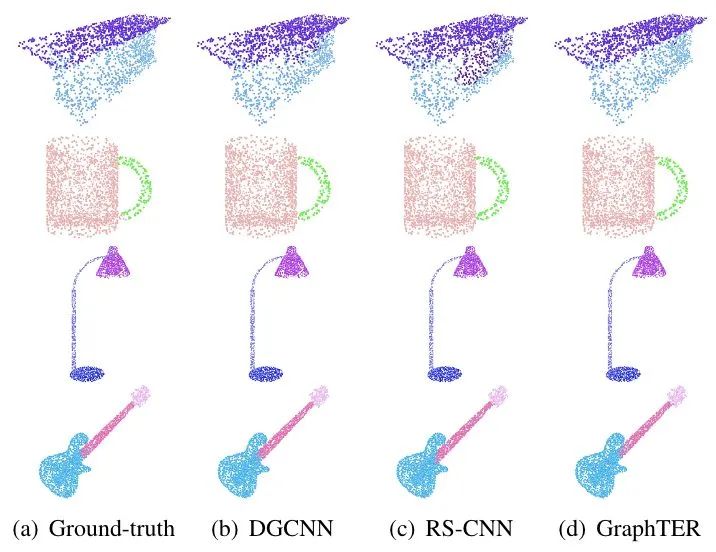
图5展示了GraphTER模型和两个全监督的方法（DGCNN和RSCNN）的3D点云分割的可视化结果。在第一行的“桌子”模型上，GraphTER模型带来了更准确的分割，并在其他模型上获得了相似的分割结果。

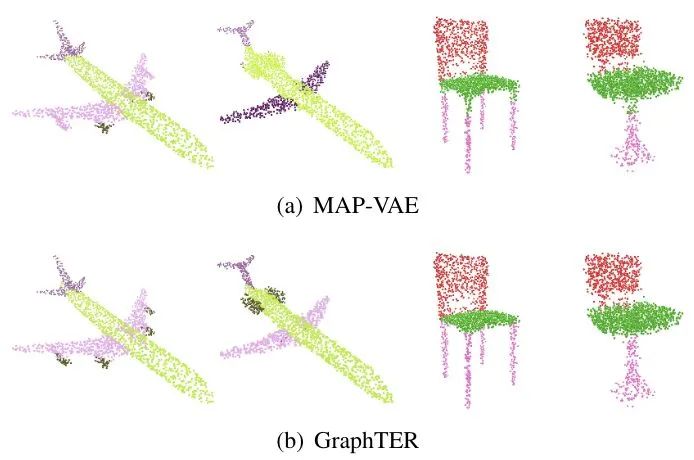
此外，我们也将GraphTER和最新的无监督方法MAP-VAE进行对别，如图6所示。与MAP-VAE相比，我们的模型能够带来更准确的分割结果，例如飞机的引擎和椅子腿的部分。

五、结论

在本文中，我们提出了一种以无监督方式自动编码节点的变换来学习图变换共变表征的方法——GraphTER。我们全局或局部地从图上采样不同的节点，然后各向同性或各向异性地进行逐节点变换，从而能够表征各种规模的图结构。通过解码这些逐节点的变换，GraphTER能够学习到图的固有表征。我们将GraphTER应用于3D点云分类和分割任务中，实验结果验证了GraphTER优于最新的无监督方法，并且大大缩小了与全监督方法性能之间的差距。我们将在未来的工作中将GraphTER模型推广到更多的应用中，例如引文网络或社交网络的节点分类。

[1] Liheng Zhang, Guo-Jun Qi, Liqiang Wang, and Jiebo Luo. AET vs. AED: Unsupervised Representation Learning by Auto-Encoding Transformations rather than Data. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), pages 2547–2555, 2019.

[2] Yue Wang, Yongbin Sun, Ziwei Liu, Sanjay E Sarma, Michael M Bronstein, and Justin M Solomon. Dynamic Graph CNN for Learning on Point Clouds. ACM Transactions on Graphics (TOG), 38(5):146, 2019.

[3] Xiang Gao, Wei Hu, and Guo-Jun Qi. GraphTER: Unsupervised Learning of Graph Transformation Equivariant Representations via Auto-Encoding Node-wise Transformations. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2020.

论文下载

在CVer公众号后台回复：GraphTER，即可下载本论文

重磅！CVer-论文写作与投稿 交流群已成立

扫码添加CVer助手，可申请加入CVer-论文写作与投稿 微信交流群，目前已满1400+人，旨在交流顶会（CVPR/ICCV/ECCV/ICML/ICLR/AAAI等）、顶刊（IJCV/TPAMI/TIP等）、SCI、EI等写作与投稿事宜。

同时也可申请加入CVer大群和细分方向技术群，细分方向已涵盖：目标检测、图像分割、目标跟踪、人脸检测&识别、OCR、姿态估计、超分辨率、SLAM、医疗影像、Re-ID、GAN、NAS、深度估计、自动驾驶、强化学习、车道线检测、模型剪枝&压缩、去噪、去雾、去雨、风格迁移、遥感图像、行为识别、视频理解、图像融合、图像检索、论文投稿&交流、PyTorch和TensorFlow等群。

一定要备注：研究方向+地点+学校/公司+昵称（如论文写作+上海+上交+卡卡），根据格式备注，可更快被通过且邀请进群