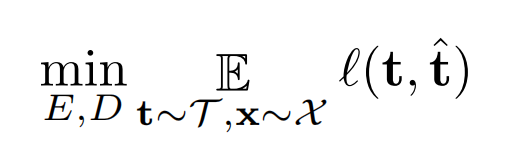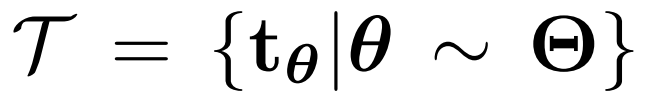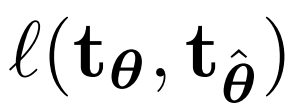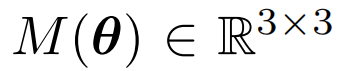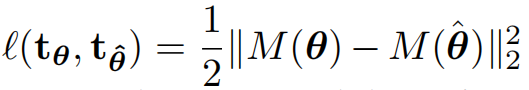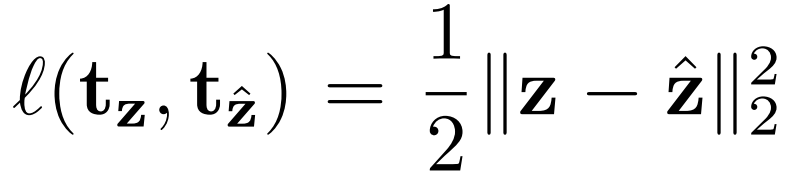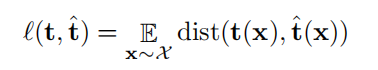华为美研所提出自动编码变换网络AET:用无监督逼近全监督效果
实验表明,与现有的无监督方法相比,AET 有了很大的改进,在 CIFAR-10、ImageNet 和 Places 数据集上取得了较好的表现。其中以 AlexNet 作为骨干网络的 Top-1 准确率(53.2%)极大地逼近了全监督方法(59.7%)。该论文已被 CVPR2019 接收。本文是 AI 前线第 69 篇论文导读,让我们一起来了解这个效果出色的无监督学习新方法。
更多干货内容请关注微信公众号“AI 前线”(ID:ai-front)
深度神经网络在图像分类、目标检测和语义分割领域取得了巨大成功,激励我们进一步探索其在各种计算机视觉任务中的全部能力。然而,训练深度神经网络通常需要大量标记数据,网络才能学习到视觉理解任务所需要的特征表示。但是许多实际场景中,只有有限数量的标记数据可用于训练网络,这极大地限制了深度神经网络的适用性。因此,越来越多的研究人员开始采用无监督的方式学习深度特征表示,以解决标签数据不足的新兴视觉理解任务。
目前最具有代表性的方法是自编码器(Auto-Encoders)和生成对抗网络(Generative Adversarial Nets)。自编码器通过训练自编码网络来输出具有足够信息的特征表示,该表示能够被对应的解码器重构成输入图像。我们将此类自编码器及其变体都归为自编码数据(Auto-Encoding Data,AED)模式。如图 1(a)所示。而 GAN 以一种无监督的方式学习特征表示,通过从输入噪声中生成图像,对抗训练生成器和判别器。生成器的输入噪声可以视为输出的特征表示,由于其包含生成对应图像的必要信息。还有一种新的方法,结合了 AED 和 GAN 的优势:为了获得每个图像的“噪声”特征表示,可以用生成器作为解码器来训练编码器,形成自动编码器体系结构。这样,在给定输入图像的情况下,编码器可以直接输出其噪声表示,通过生成器生成原始图像。
相反,我们提出通过自动编码转换(AET)而不是数据本身来学习无监督的特征表示。通过对某些图像操作算子进行采样,对图像进行变换,我们训练自编码器能从学习到的特征表示中直接重构原始图像和变换图像的操作算子。我们认为只要经过训练的特征具有足够的信息量,对图像的视觉结构进行了良好的编码。我们就可以从特征中解码出变换。与图 1 中传统的 AED 相比,AET 关注探索特征表示在不同图像变换下的动态机制,不仅揭示了静态的视觉结构,但体现了他们如何随不同的变换方式而变化。除此之外,对于 AET 框架中图像变换的形式也不受限制,因此我们探索了多种变换,从简单的图像变形到其他任何参数和非参数的变换。
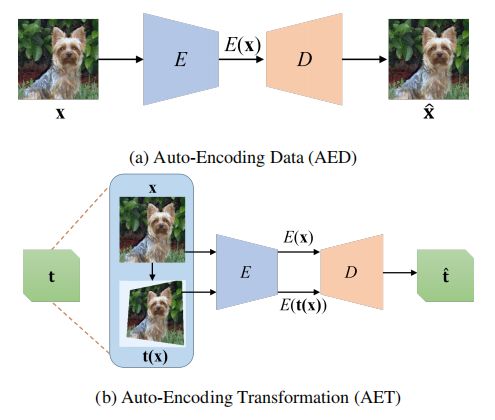
图 1:AED 与 AET 示意图。AET 尝试在输出端预测输入的变换,而 AED 在输出端预测输入的数据。AET 中,编码网络 E 提取出含有视觉结构丰富信息的特征,以解码得到输入的变换。
假设我们在分布τ中采样一个变换 t,例如图像变形,投影变换,或 GAN 引导的变换。将其应用于从分布 X 中采样得到的一张图像 x,得到 x 的变换版本 t(x)。
我们的目标是学习编码器 E:x→E(x),将给定样本 x 编码为特征表示 E(x)。同时,我们学习解码器 D:[E(x), E(t(x))]→t’,通过将原始图像和经过变换的图像的编码特征解码,得到输入变换的预测值 t’。由于对输入变换的预测是通过解码特征得到的,而不是原始图像和变换图像,它可以驱使模型提取出高质量的特征作为图像的表示。
自动编码变换(AET)的学习问题可以简化为联合训练特征编码 E 和转换网络解码器 D。我们选择一个损失函数来量化变换 t 和预测值 t’之间的误差。AET 可以通过最小化该损失函数求解:
与训练其他深度神经网络类似,E 和 D 的网络参数通过反向传播损失函数 L 的梯度,在 mini-batch 上联合更新。
许多种类的变换方式都可以轻易嵌入 AET 形式中。这里我们讨论三类变换:参数化的变换、GAN 引导的变换 和 非参数化的变换,来实例化 AET 模型。
假设我们有一簇变换:
其参数为θ。这相当于定义了参数化变换的分布,其中每个变换都可由其参数表示,而输入变换和预测变换之间的损失函数可以通过其参数的差得到:
例如放射变换和投影变换,可以表示为图像进行变换前后的同质坐标系之间的参数化矩阵:
该矩阵捕捉了由给定变换引起的几何结构变化,因此可以直接定义损失函数:
来对目标和估测变换之间的差异进行建模。
除了放射变换、投影变换这类几何变换,也可以选择其他形式的变换对网络进行实例化。比如 GAN 生成器,将输入变换到真实图像的流形上。假设生成器 G(x,z),与采样随机噪声 z 联合学习,可以对给定图片 x 的变换进行参数化。由此可以定义一个 GAN 引导的变换: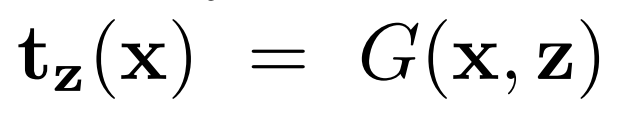
与传统的改变图像的低层级表面和几何结构信息的变换相比,GAN 引导的变换可以改变图像的高级语义。这也有助于 AET 学习到更具有表现力的特征表示。
当某个变换 t 很难参数化时,我们仍然可以通过衡量随机采样图像在变换前后的平均误差来定义损失函数:
对于输入的非参数变换 t,我们也需要解码网络输出对变换的预测值 t‘。这一步可以通过选择一个参数化的变换 tθ作为 t‘,作为 t 的估测值。尽管非参数的变换 t 不属于参数化变换的空间,但是这样的近似已经足够用于无监督学习,因为我们的最终目标并不是获取对输入变换的精准估计,而是学习到能够在参数化变换空间中给出最佳估计的好的特征表示。
我们发现多种变换都可以用于训练 AET,但是在本文中我们主要关注参数化变换,因为他们不需要训练额外的模型(GAN 引导的变换),也不需要选择附加的变换对非参数形式进行近似(非参数变换)。这样在实验中可以和其他非监督方法进行直接明了的对比。
在这一部分,我们在 CIFAR-10,ImageNet 和 Places 数据库上测试所提出的 AET 模型。无监督学习方法通常根据使用学习到的特征的分类表现对其进行评价。
我们首先在 CIFAR-10 数据库上对 AET 模型进行评价。我们采用了两个不同的变换:放射变换(affine)和投影变换(projective)来训练 AET,分别将训练得到的模型命名为 AET-affine 和 AET-project。
我们采用 NIN(Network-In-Network)结构。如图 2 上半部分所示,NIN 由 4 个卷积块组成,每个包含 3 个卷积层。AET 有 2 个 NIN 分支,分别将原始图像和变形图像作为输入。两个分支第四个卷积块的输出进行相连,并平均池化成一个 384-d 的特征矢量。在最后附加一个全连接层对输入的变换进行预测。两个分支共享网络权重,作为编码网络,对输入图像生成特征表示。(训练细节、以及放射变换和投影变换的具体参数请参考论文原文。)
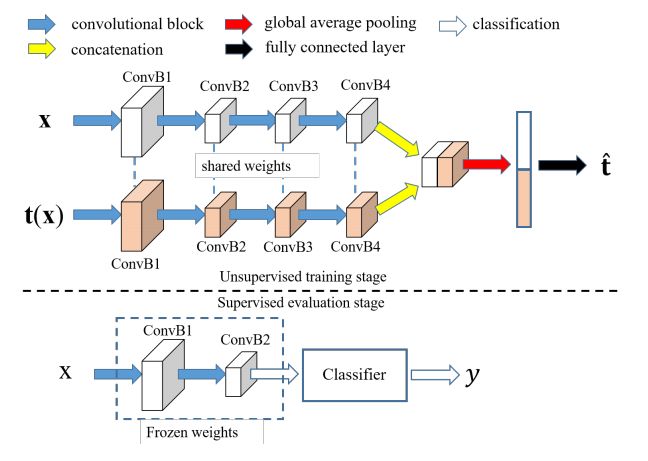
图 2:在 CIFAR-10 数据集上训练和衡量的 AET 模型的网络结构示意图。
为了评价无监督模型学习到特征的质量,一般利用学习到的特征训练分类器。根据现有评价准则,我们在第二个卷积块上建立一个分类器,如图 2 底部所示,将前两个卷积块固定,并利用标注样本在其上训练分类器。我们通过使用 AET 特征训练基于模型的和无模型的分类器,对分类结果进行评测。
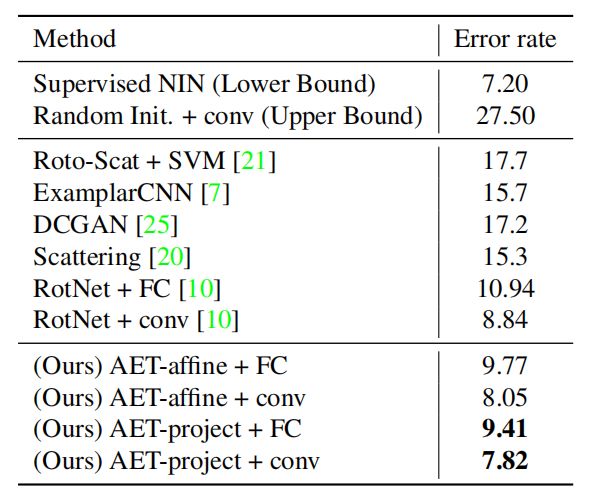
表 1:CIFAR-10 数据库上无监督特征学习方法的对比。
表 1 给出了 CIFAR-10 数据集 AET 模型和其它全监督以及无监督方法的对比。从表中可以看到,无监督 AET 模型 + 卷积分类器几乎达到了其对应的全监督 NIN 的错误率(7.82% vs. 7.2%)。AET 也超过了其他无监督方法的表现,体现了 AET 能够在无监督网络的训练中更有效地探索图像变换的信息。由于 RotNet 和 AET 采用的是同样的网络和分类器,我们将 RotNet 作为比较基线。从结果中可以看出,利用 AET 学到的特征训练的全连接(FC)和卷积分类器的分类结果都完胜 RotNet。

表 2:RotNet 与 AET 在 CIFAR-10 数据集的效果对比。
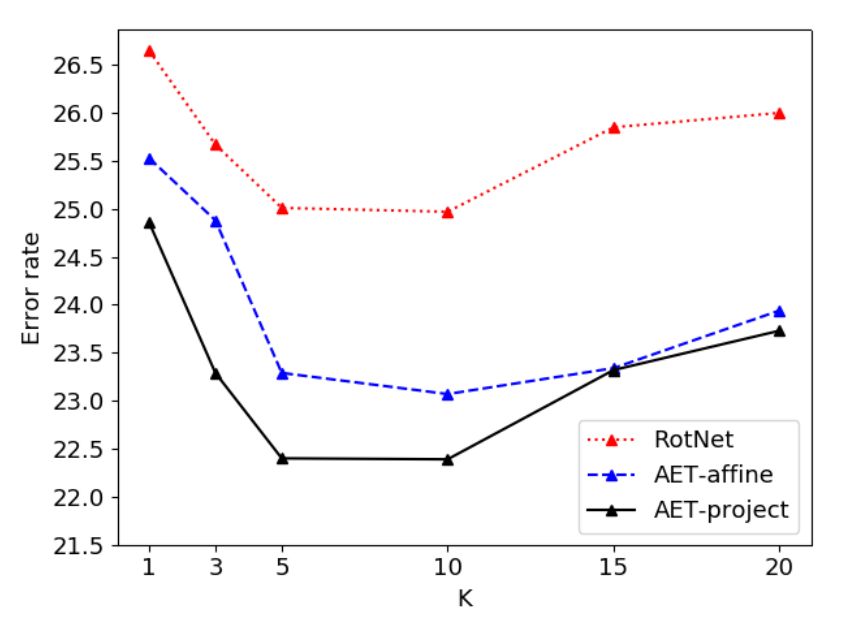
图 3:不同模型的 KNN 误差率随近邻数量 K 的变化曲线图。
图 3 中,我们比较了 KNN 近邻数量 K 对结果的影响。AET-project 依然取得了最好的表现。KNN 分类器的结果体现了利用 AET 模型学习到的无监督特征在无类标数据的情况下训练分类器的优势。
我们进一步在 ImageNet 数据集上验证 AET 的效果。我们使用 AlexNet 作为骨干网络来学习无监督特征,采用投影变换作为图像变换实例。
我们采用两个 AlexNet 网络分支,共享权重,分别采用原始图像和变换图像作为网络输入,训练 AET-project 模型。两个分支的倒数第二个全卷积层的特征连接起来,经过输出层,得到 8 个投影变换的参数(训练细节请参考论文原文)。
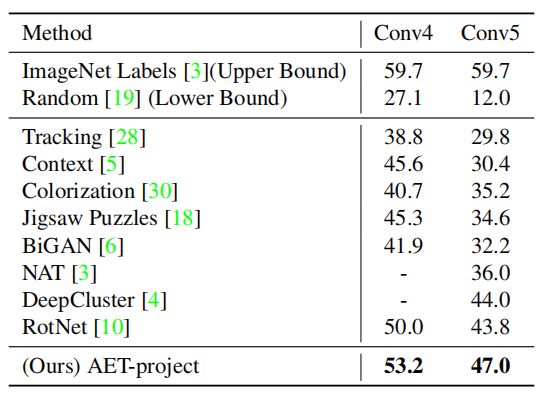
表 3:ImageNet 数据集非线性层的 Top-1 准确率。
我们采用了两种设置:Conv4 和 Conv5。它们分别表示在无监督训练后,将 AlexNet 从底层的卷积层到 Conv4、或到 Conv5 的部分固定,然后利用标注数据训练网络的剩余部分。从结果中可以看出,两种设置下 AET 模型的表现都优于其他无监督模型。
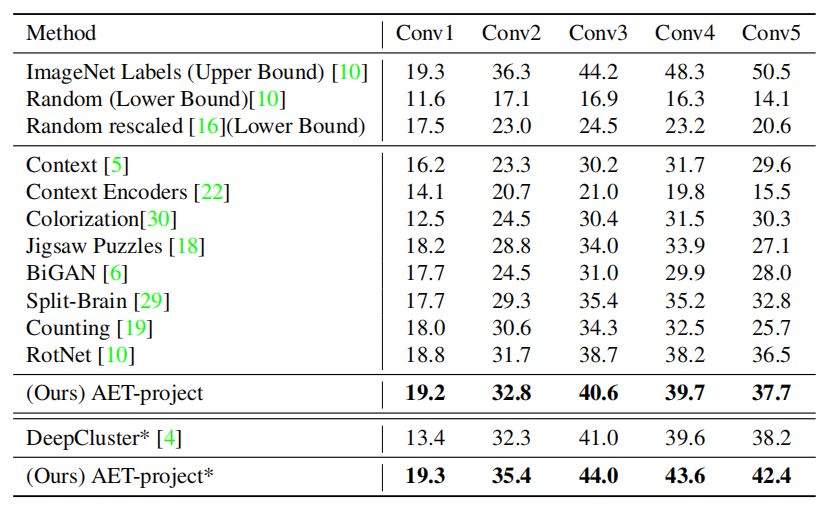
表 4:ImageNet 数据集线性层的 Top-1 准确率。
我们在不同数量的卷积层上训练了一个 1000 个通道的线性分类器进行测试,表 4 给出了实验结果。从表中可以看出 AET 学习到的特征在线性分类器上的表现也超越了其他无监督方法。
我们在 Places 数据集上进行了实验。如表 5 所示,我们评测了在 ImageNet 数据集上进行预训练的无监督模型,然后利用 Places 的标注数据训练单层的逻辑回归分类器。我们通过这个实验评估了无监督特征从一个数据集到另一个的可扩展性。我们的模型依然基于 AlexNet。我们也对比了利用 Places 数据集的标注数据和 ImageNet 数据集标注数据的全监督模型。结果显示 AET 模型的表现优于其他无监督模型。
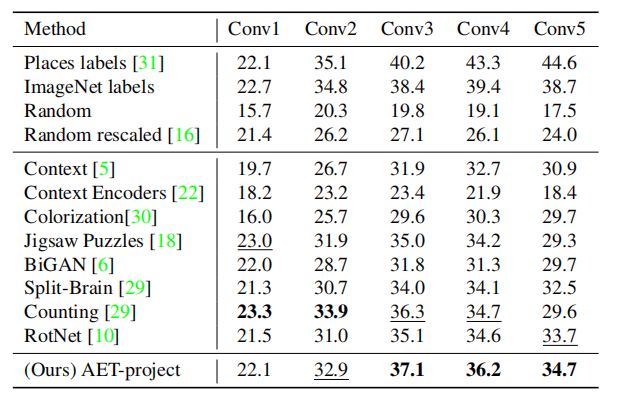
表 5:Places 数据集线性层的 Top-1 准确率
尽管我们的最终目标是学习到好的图像特征表示,我们也研究了预测的变换的准确度,以及它和监督学习分类器性能的关系。
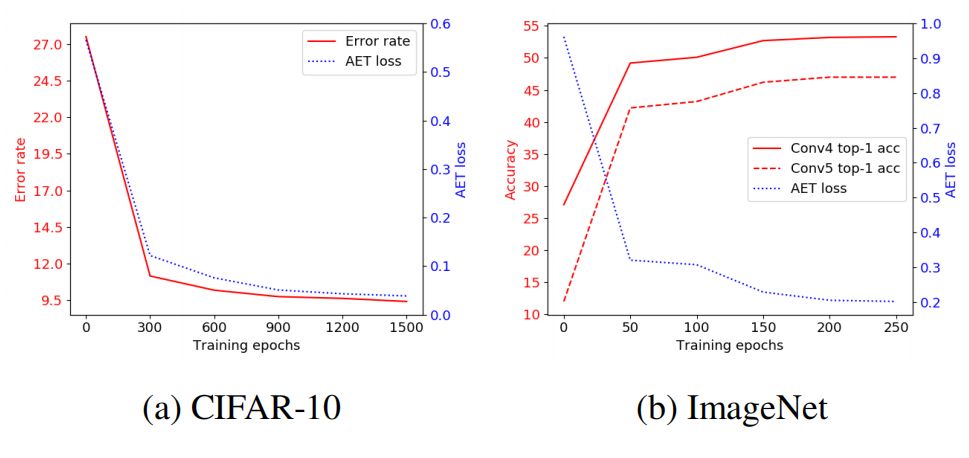
图 4:错误率(top-1 准确率)vs. AET 损失在 CIFAR-10 和 ImageNet 数据集上随训练 epoch 变化曲线图。
如图 4 所示,变换预测的损失(AET 模型训练最小化的损失)与分类误差和 Top-1 准确率都较为匹配。更好的变换预测准确度代表着所学习到的特征能取得更好的分类结果。

图 5:原始图像(顶部),经过变换的输入图像(中部),经过 AET 模型预测变换的图像(底部)。
在图 5 中,我们也对比了原始图像、变换图像,以及 AET 模型预测变换的图像。这些样例体现了模型能很好地从编码特征中解码出变换,从而得到的无监督表示能够在分类实验中有较好的表现。
在这篇论文中,我们提出了一个与传统的自动编码数据方法(AED)相对的自动编码变换方法(AET),用于无监督训练神经网络。通过在网络输出端估测随机采样的变换,AET 驱使编码器学习好的图像表示,能够包含关于原始图像和变换图像的视觉结构信息。多种变换都可以融合到该框架下,实验结果验证了该方法的表现相对于其他方法有了显著提高,大大缩短了与全监督方法的差距。
论文原文:https://arxiv.org/pdf/1901.04596.pdf
喜欢这篇文章吗?点一下「好看」再走👇