推荐系统之FM算法原理及实现(附代码)
导读
Factorization Machine
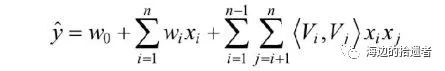
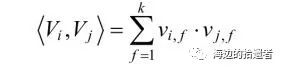
损失函数
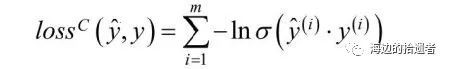
交叉项处理
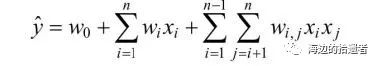
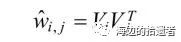
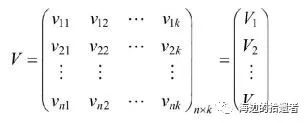
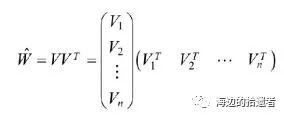
梯度下降法
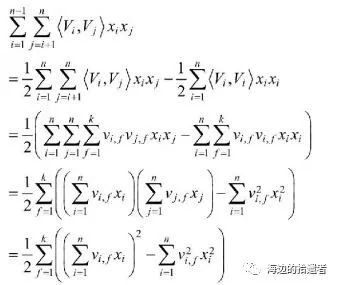
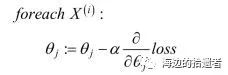
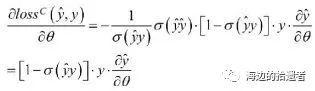
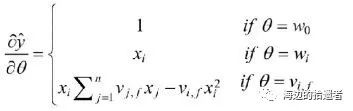
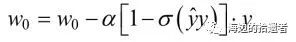
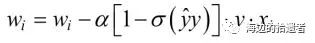
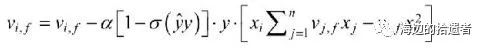
import numpy as np
def fm_sgd(dataMatrix, classLabels, k, max_iter, alpha):
'''input: dataMatrix特征
classLabels标签
k v的维数
max_iter最大迭代次数
alpha学习率
output: w0,w,v权重'''
m, n = np.shape(dataMatrix)
# 1、初始化参数
w = np.zeros((n, 1))
w0 = 0
v = initialize_v(n, k)
# 2、训练
for it in range(max_iter):
for x in range(m):
inter_1 = dataMatrix[x] * v
inter_2 = np.multiply(dataMatrix[x], dataMatrix[x]) * \
np.multiply(v, v)
# 完成交叉项
interaction = np.sum(np.multiply(inter_1, inter_1) - inter_2) / 2.
p = w0 + dataMatrix[x] * w + interaction
loss = sigmoid(classLabels[x] * p[0, 0]) - 1
w0 = w0 - alpha * loss * classLabels[x]
for i in range(n):
if dataMatrix[x, i] != 0:
w[i, 0] = w[i, 0] - alpha * loss * classLabels[x] * dataMatrix[x, i]
for j in range(k):
v[i, j] = v[i, j] - alpha * loss * classLabels[x] * \
(dataMatrix[x, i] * inter_1[0, j] -\
v[i, j] * dataMatrix[x, i] * dataMatrix[x, i])
# 计算损失函数的值
if it % 1000 == 0:
print("\t------- iter: ", it, " , cost: ", \
Cost(Prediction(np.mat(dataMatrix), w0, w, v), classLabels))
return w0, w, v
import numpy as np
from numpy import normalvariate
def sigmoid(x):
return 1.0 / (1 + np.exp(-x))
def initialize_v(n, k):
'''input: n特征的个数
k超参数
output: v辅助矩阵'''
v = np.mat(np.zeros((n, k)))
for i in range(n):
for j in range(k):
v[i, j] = normalvariate(0, 0.2)
return v
def Prediction(dataMatrix, w0, w, v):
'''input: dataMatrix特征
w常数项权重
w0一次项权重
v辅助矩阵
output: result预测结果'''
m = np.shape(dataMatrix)[0]
result = []
for x in range(m):
inter_1 = dataMatrix[x] * v
inter_2 = np.multiply(dataMatrix[x], dataMatrix[x]) * \
np.multiply(v, v)
# 完成交叉项
interaction = np.sum(np.multiply(inter_1, inter_1) - inter_2) / 2.
p = w0 + dataMatrix[x] * w + interaction
pre = sigmoid(p[0, 0])
result.append(pre)
return result
def Cost(predict, classLabels):
'''input: predict预测值
classLabels标签
output: error损失函数值'''
m = len(predict)
error = 0.0
for i in range(m):
error -= np.log(sigmoid(predict[i] * classLabels[i] ))
return error
到这里整个流程基本就结束了~
推荐阅读
[1]. 由Logistic Regression所联想到的...
[2]. 推荐系统之矩阵分解家族
来都来了,点个在看再走吧~~~

登录查看更多
相关内容
Arxiv
4+阅读 · 2018年11月26日