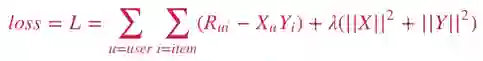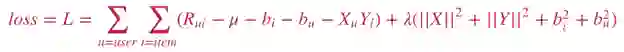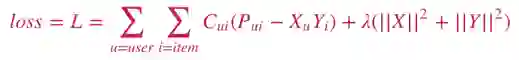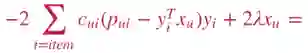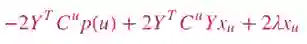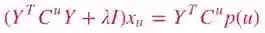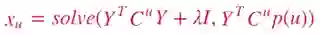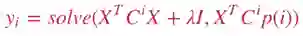推荐系统经典技术：矩阵分解

2017 年 10 月 10 日 LibRec智能推荐 马辰

在2007年，Netflix公布了一项推荐算法的比赛，根据用户对电影的评分历史，预测用户对没有看过的电影的评分。如果有队伍能在测评指标上超过Netflix官方的推荐系统——“Cinematch” 10%以上，将会被奖励100万美元。最终，在2009年，一支名为“BellKor's Pragmatic Chaos”的队伍以超过“Cinematch” 10.06%的成绩获得全部奖金。在Netflix比赛的推动下，矩阵分解方法大放异彩，许多队伍采用矩阵分解的方法都取得了不错的效果。今天我们将介绍推荐系统中的经典算法——矩阵分解。

矩阵分解算法主要作用在用户-物品评分矩阵上，其主要思路是将评分矩阵分解成两个低维的矩阵，分别用来刻画用户和物品的特征，再由这两个低维矩阵的内积来重建用户对未评分物品的评分。在通常情况下，评分矩阵有两种类型：Explicit Feedback 和 Implicit Feedback。

Explicit Feedback

用户显式地用评分表达对物品的喜欢或不喜欢。如在豆瓣电影中，用户可以用5星表达自己对电影的喜爱，也可以用1星表达对电影的不喜爱。在文章Matrix Factorization Techniques for Recommender Systems[1] 中指出，最基本的处理Explicit Feedback的模型可以表达为：

其中，R是已知的用户对物品的评分，X是用户的latent factor，Y是物品的latent factor，lambda是正则化系数。更复杂的加入了用户和物品偏置项的模型可以表达为：

以上两种模型均可通过SGD (stochastic gradient descent) 或ALS (altering least square) 来求解。

可以参考LibRec中的 BiasedMFRecommender.java

Implicit Feedback

用户对物品的喜好可以通过用户在物品上的行为侧面反映。如在Point-of-Interest推荐中，用户在某个地点的check-in次数可以侧面反映用户对这个地点的喜爱程度。大多数推荐系统是处理implicit feedback的，因为用户的行为比用户的偏好要更容易观察得到。当然在这样的数据中噪声也更大，不容易推测出用户的喜好。

在论文Collaborative Filtering for Implicit Feedback Datasets [2] 中叙述的weighted alternating least squares模型是一种非常经典地处理implicit feedback的方法。这个方法与上述处理explicit feedback最大的不同之处是，这种方法将所有的用户与物品的交互都视为positive sample，用户与物品交互的次数反映了用户这个物品感兴趣的程度 (confidence)。这个模型可以被表示为：

其中P是一个二值化的矩阵，用来表达用户是否和物品有交互。C是confidence矩阵，由用户和物品的交互次数矩阵得到，次数越多相应的值越大，用来表达用户对物品的感兴趣程度。对于这个损失函数的优化可以通过ALS来实现，具体求解过程如下：

在导数等于0时，我们可以得到关于X的最优解：

通过求解上述线性方程，可以得到xu 的值：

相应地，yi 可以通过下式得到：

可以参考LibRec中的 WRMFRecommender.java

Reference:

Matrix Factorization Techniques for Recommender Systems. Yehuda Koren, Robert M. Bell, Chris Volinsky. IEEE Computer 42(8): 30-37 (2009).
Collaborative Filtering for Implicit Feedback Datasets. Yifan Hu, Yehuda Koren, Chris Volinsky. ICDM 2008: 263-272.