【干货】终极入门 马尔可夫网络 (Markov Networks)——概率图模型

今天我们把注意力放到无向图模型，以及马尔可夫网络 (Markov Networks)。 事实上之所以叫做无向图模型，只是因为概率图中的边可以是双向的：

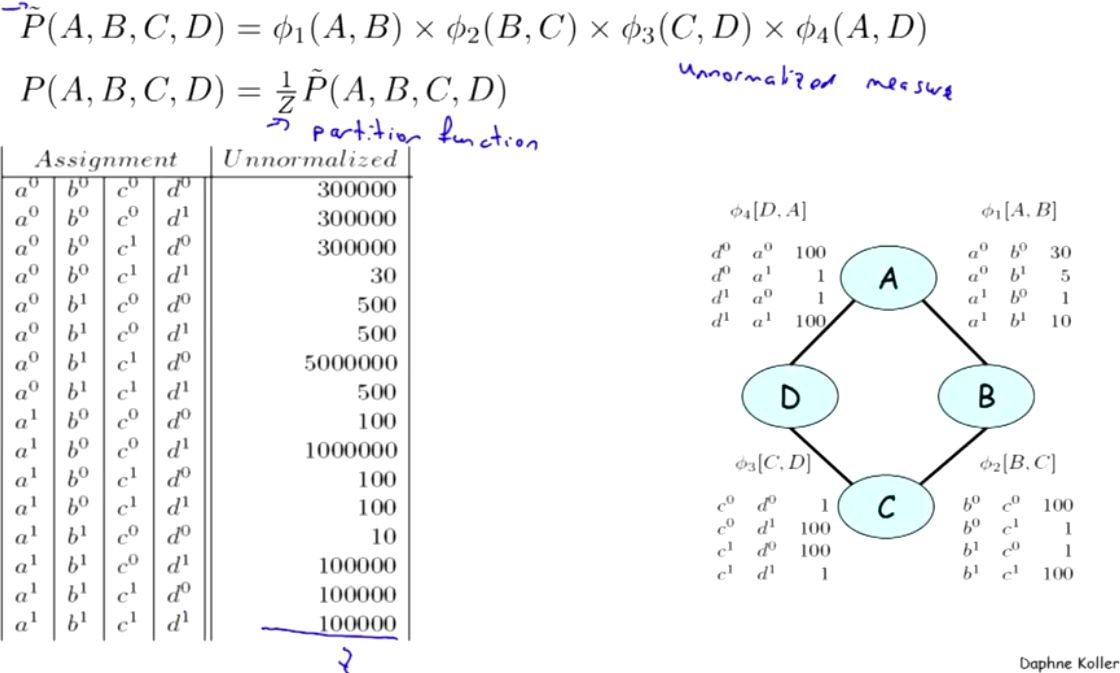
在这里，就是所有可能性值的求和：

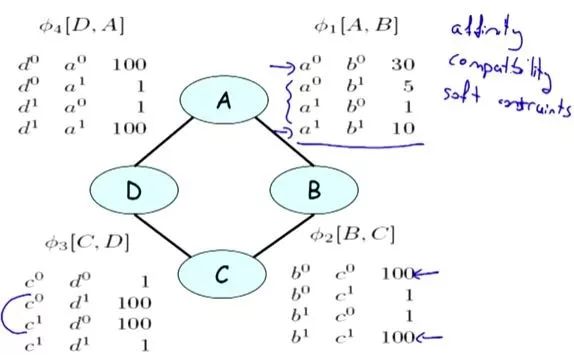
唯一与马尔可夫网络不同的是，这里每个factor中的Di可以是多元的。

所有可以总结，

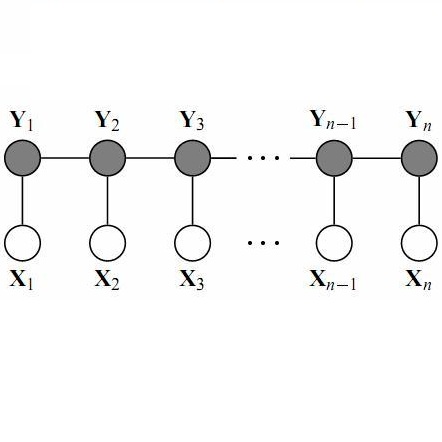
最后我还要介绍一种非常常用的马尔可夫网络变形：条件随机场（CRF）。

与马尔可夫网络唯一不同的是，条件随机场（CRF）求partition function的时候是仅仅对一个变量求和的，最后求的是在X情况下的条件概率，而不是联合概率：

这就在建模时有许多有意思的结果：

1. CRF是很不错的判别模型， 对数几率回归就是其中一种。

2. CRF可以把整个图模型的局部特征函数转化为全局特征函数，从而写成条件随机场的权重向量和特征向量的内积形式。这就可以每次只关心一个特征。再把所有全局特征集中起来一起考虑。

如判别上图中的动物是奶牛，我们首先把整个图“切”成一块块的“小图”。

如果用贝叶斯网络或者朴素贝叶斯构建这些“小图”，就需要把每个“小图”的所有特征都考虑进去，这在最终求联合概率时将会非常复杂。而条件随机场解决了这个问题，我们不需要费力考虑每个小块之间的关系。

相反，我们可以先关注所有小块的颜色亮暗比的分布，再关注所有小块纹理粗糙度的分布，然后考虑动物边界是不是明显有4只脚，最后把这些因素都合起来，判别这个动物是不是奶牛？这样，是不是在数学上更好处理了？

转自：机器学习算法与自然语言处理

完整内容请点击“阅读原文”